
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания для самостоятельной работы. 1. С помощью переноса начала координат привести уравнение линии к каноническому виду, определить тип линии и построить ее изображение:
|
|
1. С помощью переноса начала координат привести уравнение линии к каноническому виду, определить тип линии и построить ее изображение:
а) 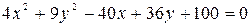 ;
;
б) 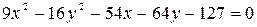 ;
;
в) 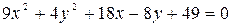 ;
;
г) 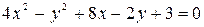 .
.
2.. С помощью переноса начала координат привести уравнение линии к каноническому виду, определить тип линии и построить ее изображение:
а) 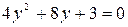 ;
;
б) 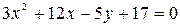 ;
;
в) 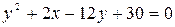 .
.
3. Привести уравнение к каноническому виду, определить тип линии и построить ее изображение:
а) 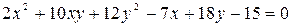 ;
;
б) 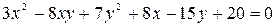 ;
;
в) 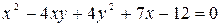 ;
;
г)  .
.
Оглавление
| Стр. | |
| Методические рекомендации по работе с электронным вариантом лекций …………………………………………………………………… | |
| Список рекомендуемой литературы …………………………………… | |
| Элементы векторной алгебры……………………………………….. | |
| Лекция 1. Векторы. Линейные операции над векторами …………….. | |
| §1. Понятие вектора ………………………………….. | |
| §2. Сложение и вычитание векторов ……………….. | |
| §3. Умножение вектора на число …………………… | |
| Лекция 2. Линейная зависимость векторов …………………………… | |
| §4. Линейная зависимость векторов и ее свойства ………… | |
| Лекция 3. Базис. Координаты вектора ………………………………… | |
| §5. Базис. Координаты вектора в данном базисе и их свойства ………………………………………………………… | |
| Лекция 4. Нелинейные операции над векторами …………………….. | |
| §6. Скалярное произведение двух векторов ……………….. | |
| Лекция 5. Нелинейные операции над векторами …………………….. | |
| §7. Понятие об ориентации пространства и плоскости ……. | |
| §8. Векторное произведение двух векторов ………………… | |
| Лекция 6. Нелинейные операции над векторами ……………………... | |
| §9. Смешанное произведение трех векторов ……………….. | |
| Метод координат на плоскости и в пространстве ………………… | |
| Лекция 7. Аффинная и прямоугольная декартова системы координат | |
| §10. Понятие аффинной и прямоугольной декартовой систем координат ………………………………………….. | |
| §11. Основные аффинные и метрические задачи …………. | |
| Лекция 8. Формулы преобразования координат ……………………… | |
| §12. Преобразование аффинной системы координат ……… | |
| §13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат ……. | |
| §14. Полярные координаты …………………………………. | |
| Прямая линия на плоскости | |
| Лекция 9. Прямая в аффинной системе координат …………………… | |
| §15. Различные уравнения прямой ……………………….…. | |
| §16. Общее уравнение прямой и его частные случаи ……... | |
| §17. Основные аффинные задачи, связанные с прямой на плоскости (обзор) ………………………………………. | |
| Лекция 10. Прямая в прямоугольной декартовой системе координат | |
| §18. Уравнение прямой, заданной точкой и вектором нормали ……………………………………………………… | |
| §19. Основные метрические задачи, связанные с прямой на плоскости ………………………………………………… | |
| Плоскости и прямые в пространстве……………………………….. | |
| Лекция 11. Плоскость в аффинной системе координат ………………. | |
| §20. Различные уравнения плоскости в аффинной системе координат ……………………………………………….. | |
| §21. Общее уравнение плоскости ………………………….. | |
| §22. Лемма о параллельности вектора и плоскости. Частные случаи общего уравнения плоскости ……………. | |
| §23. Основные аффинные задачи, связанные с плоскостью (обзор) ………………………………………………….. | |
| Лекция 12. Плоскость в прямоугольной системе координат ……….. | |
| §24. Плоскость в прямоугольной системе координат. Основные метрические задачи, связанные с плоскостью | |
| Лекция 13. Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве …………………………………. | |
| §25. Различные уравнения прямой в пространстве ………… | |
| §26. Основные аффинные задачи на прямые и плоскости … | |
| §27. Основные метрические задачи на прямые и плоскости в пространстве …………………………………………….. | |
| Линии второго порядка……………………………………………….. | |
| Лекция 14. Эллипс. Гипербола. Парабола …………………………….. | |
| § 28. Эллипс …………………………………………………... | |
| § 29. Гипербола ……………………………………………….. | |
| § 30. Парабола ………………………………………………… | |
| Лекция 15. Понятие о классификации линий второго порядка. Приведение общего уравнения линии второго порядка к каноническому виду ………………………………………….. | |
| § 31. Понятие о классификации линий второго порядка …... | |
| § 32. Приведение общего уравнения линии второго порядка к каноническому виду …………………………………. |
Date: 2015-07-11; view: 458; Нарушение авторских прав