Гипербола

Гиперболой называется множество всех точек плоскости, абсолютное значение разности расстояний каждой из которых до данных точек 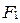и 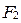равно длине данного отрезка 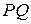, где .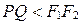

Коротко можно записать определение гиперболы 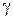так:

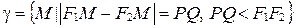. (39)

Точк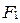и и 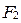называются фокусами гиперболы, а расстояние между ними - фокальным расстоянием.

Если 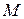- точка данной гиперболы, то отрезк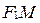и и (а также их длины) называются фокальными радиусами точки .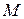

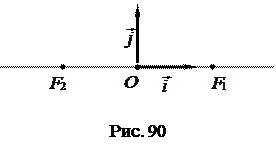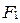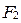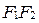Пусть на плоскости даны две различные точки и . Обозначим через се­редину отрезка . Рассмотрим прямоугольную декартову систему координат 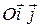, где 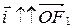(рис. 90).

Выведем уравнение гиперболы 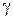с фо­кусам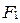и и 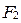в системе координат .

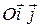Пусть .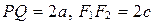

Замечание. Так как 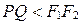, то для гиперболы всегда 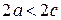, т.е.

.

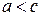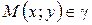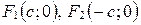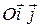Пусть . Так как в , то

.

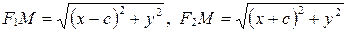По определению гиперболы 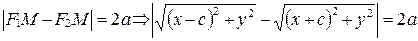. Преобразуем это уравнение:

;

;

;

;

;

.

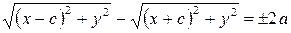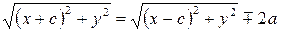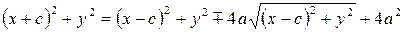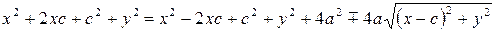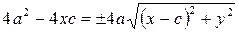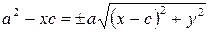Возведем обе части последнего уравнения в квадрат:

;

;

.

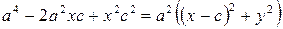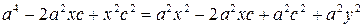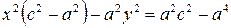Разделим обе части этого уравнения на :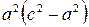

.

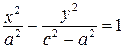Так как для гиперболы 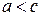, то 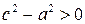. Положим 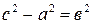. Тогда

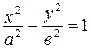, где 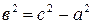. (40)

Итак, доказано, что если 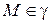, то координаты точки 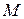удовлетворяют урав­нению (40).

Докажем, что если координаты точки 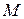удовлетворяют уравнению (40), то она принадлежит гиперболе .

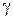Пусть 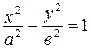, где 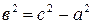, 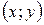- координаты точки .

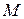Найдем 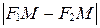. Выразим 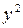из уравне­ния :

.

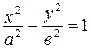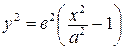Найдем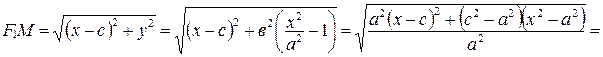

.

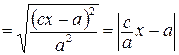Аналогично .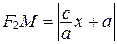

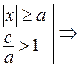
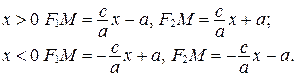
Тогда .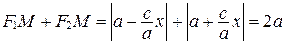

Из условия (39) следует, что .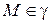

Итак, уравнение (40) есть уравнение гиперболы. Оно называется каноническим уравнением гиперболы.

Пользуясь каноническим уравнением гиперболы, докажем геометрические свойства гиперболы, которые понадобятся для построения изображения гиперболы.

Date: 2015-07-11; view: 542; Нарушение авторских прав