
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

К каноническому виду
|
|
По виду общего уравнения трудно определить тип линии второго порядка. Для этого общее уравнение линии второго порядка надо привести к каноническому виду. Это делают с помощью преобразования прямоугольной декартовой системы координат 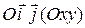 , в которой дано общее уравнение (43) линии. С помощью поворота координатных векторов и переноса начала получают каноническую систему координат
, в которой дано общее уравнение (43) линии. С помощью поворота координатных векторов и переноса начала получают каноническую систему координат  , в которой уравнение данной линии второго порядка имеет канонический вид.
, в которой уравнение данной линии второго порядка имеет канонический вид.
Итак, пусть линия второго порядка 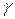 задана в системе
задана в системе 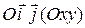 общим уравнением
общим уравнением 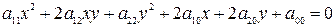 .
.
Если 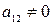 , то приведение общего уравнения линии
, то приведение общего уравнения линии 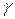 к каноническому виду происходит в два этапа:
к каноническому виду происходит в два этапа:
I этап. С помощью поворота координатных векторов освобождаются от члена, содержащего произведение 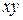 . Угол поворота
. Угол поворота 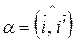 находят следующим образом:
находят следующим образом:
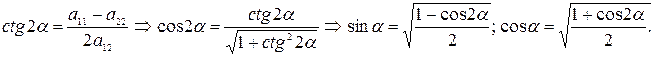
Тогда координаты координатных векторов 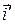 и
и 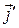 в системе
в системе  будут находиться так:
будут находиться так:
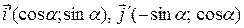 . (44)
. (44)
Записываем формулы поворота координатных векторов на угол 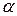 :
:
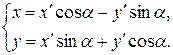 (45)
(45)
Подставляем  и
и 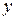 из формул (45) в общее уравнение линии
из формул (45) в общее уравнение линии 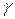 . После преобразований исчезает член
. После преобразований исчезает член 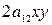 . Получаем уравнение линии
. Получаем уравнение линии 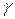 в промежуточной системе координат
в промежуточной системе координат 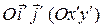 .
.
II этап. Выделяем полные квадраты при 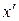 и
и 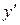 и совершаем перенос начала
и совершаем перенос начала  в точку
в точку 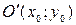 по формулам
по формулам
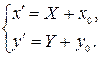 (46)
(46)
Координаты  точки
точки 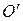 вычислены в системе
вычислены в системе 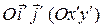 .
.
Подставляем 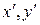 из формул (46) в уравнение линии
из формул (46) в уравнение линии 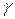 в системе
в системе 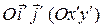 . После преобразований получаем каноническое уравнение линии
. После преобразований получаем каноническое уравнение линии 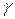 в новой системе
в новой системе  и определяем ее вид.
и определяем ее вид.
Строим старую систему координат 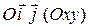 , промежуточную
, промежуточную 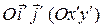 , новую
, новую  и линию
и линию 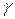 по ее каноническому уравнению в системе
по ее каноническому уравнению в системе  .
.
Замечание 1. При переходе ко II этапу возможны следующие случаи:
1.Уравнение содержит переменные 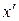 и
и 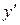 во второй степени. Тогда выделяются полные квадраты при
во второй степени. Тогда выделяются полные квадраты при 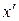 и
и 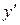 . В результате может получиться каноническое уравнение эллипса, гиперболы, мнимого эллипса, пары пересекающихся прямых или пары мнимых пересекающихся прямых.
. В результате может получиться каноническое уравнение эллипса, гиперболы, мнимого эллипса, пары пересекающихся прямых или пары мнимых пересекающихся прямых.
2. Уравнение содержит только одну переменную во второй степени, а другую – только в первой. Тогда после выделения полного квадрата при той переменной, которая стоит во второй степени, с помощью переноса начала освобождаются от свободного члена. В результате получится каноническое уравнение параболы.
3. Уравнение содержит только одну переменную и в первой, и во второй степени, другая переменная отсутствует. Выделяем полный квадрат и получаем каноническое уравнение пары параллельных прямых, пары мнимых параллельных прямых или пары совпавших прямых.
Замечание 2. Если в общем уравнении линии 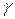
 , то приведение общего уравнения к каноническому виду начинают сразу со II этапа.
, то приведение общего уравнения к каноническому виду начинают сразу со II этапа.
Рассмотрим конкретный пример.
Задача. Привести общее уравнение 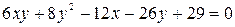 линии
линии 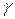 к каноническому виду, определить вид линии
к каноническому виду, определить вид линии 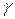 и построить ее изображение.
и построить ее изображение.
Решение. I этап. Из общего уравнения линии  находим
находим  .
.
Найдем угол поворота координатных осей:
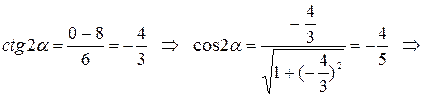
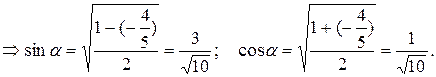
Находим координаты координатных векторов  и
и 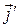 в системе координат
в системе координат  :
:
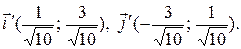
Записываем формулы поворота координатных векторов на угол 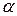 :
:
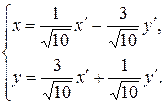
Подставляем  и
и 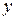 из полученных формул в общее уравнение линии
из полученных формул в общее уравнение линии  :
:

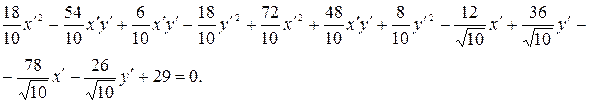
После приведения подобных получаем уравнение линии 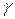 в системе координат
в системе координат 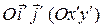 :
:
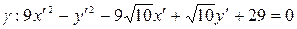 .
.
II этап. Найдем формулы переноса начала координат. Для этого выделим полные квадраты при 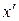 и
и 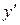 :
:

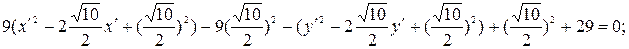
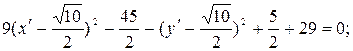
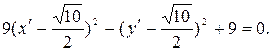
Положим

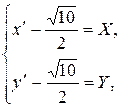
тогда получаем формулы переноса начала:
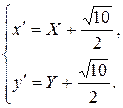
При этом точка  переходит в точку
переходит в точку 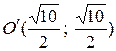 , координаты которой найдены в системе
, координаты которой найдены в системе 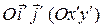 .
.
Линия 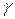 в системе
в системе  будет иметь уравнение
будет иметь уравнение
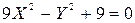 .
.
Приведем это уравнение к каноническому виду:
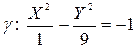 .
.
Следовательно, 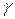 - гипербола с мнимой осью
- гипербола с мнимой осью 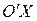 .
.
Последовательность построения изображения гиперболы 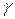 такова:
такова:
а) Строим старую систему координат 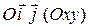 .
.
б) Строим промежуточную систему координат 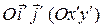 . При этом чтобы точно совершить поворот координатных векторов
. При этом чтобы точно совершить поворот координатных векторов 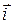 и
и 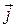 на угол
на угол 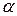 , построим сначала вспомогательные векторы
, построим сначала вспомогательные векторы 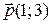 и
и 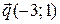 , которые будут коллинеарны векторам
, которые будут коллинеарны векторам 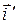 и
и 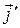 соответственно (на чертеже эти векторы не показаны, а построены лишь их концы – точки с координатами
соответственно (на чертеже эти векторы не показаны, а построены лишь их концы – точки с координатами 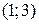 и
и 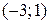 (рис. 98). Тогда единичные векторы
(рис. 98). Тогда единичные векторы 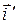 и
и 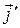 будут сонаправлены с векторами
будут сонаправлены с векторами 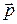 и
и 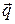 , а оси координат
, а оси координат  и
и 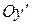 пройдут через точку
пройдут через точку  и точки
и точки 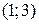 и
и 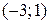 соответственно (рис. 98).
соответственно (рис. 98).
в) Строим новую систему координат  .
.
 г) Строим линию
г) Строим линию 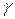 по ее каноническому уравнению в системе координат
по ее каноническому уравнению в системе координат  (рис. 99).
(рис. 99).
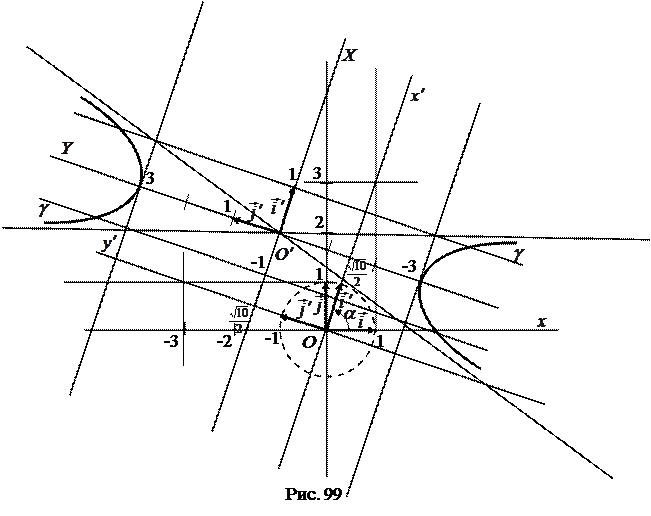 |
Date: 2015-07-11; view: 678; Нарушение авторских прав