
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства гиперболы
|
|
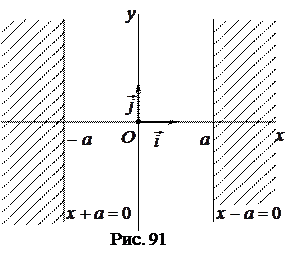 |
1°. Из уравнения (40) следует, что 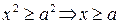 или
или 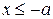 . Следовательно, все точки гиперболы лежат вне полосы, ограниченной прямыми
. Следовательно, все точки гиперболы лежат вне полосы, ограниченной прямыми  и
и 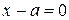 (рис. 91).
(рис. 91).
2°. Симметрия относительно начала координат и осей координат.
Пусть 
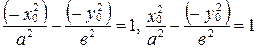 и
и 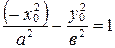 . Из первого тождества следует, что
. Из первого тождества следует, что  , из второго – что
, из второго – что 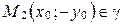 , из третьего – что
, из третьего – что 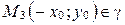 , а это означает, что гипербола
, а это означает, что гипербола 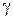 симметрична относительно начала координат, оси
симметрична относительно начала координат, оси 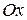 и оси
и оси 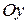 соответственно. Таким образом, точка
соответственно. Таким образом, точка  является центром симметрии, оси
является центром симметрии, оси 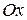 и
и 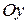 - осями симметрии гиперболы
- осями симметрии гиперболы 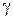 .
.
Прямая, проходящая через фокусы, называется действительной осью симметрии, а перпендикулярная к ней ось – мнимой осью симметрии гиперболы.
3°. Точки пересечения гиперболы с осями симметрии.
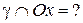
Чтобы найти точки пересечения гиперболы 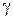 с осью
с осью 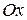 , надо решить систему их уравнений:
, надо решить систему их уравнений: 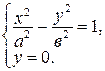
Решая систему, получаем:  .
.
Аналогично находим, что 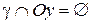 .
.
Точки пересечения гиперболы со своими осями симметрии называются вершинами гиперболы. Таким образом, гипербола имеет две вершины.
Отрезки 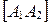 и
и 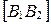 называются соответственно действительной и мнимой «осями» гиперболы, а положительные числа
называются соответственно действительной и мнимой «осями» гиперболы, а положительные числа 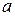 и
и 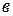 - действительной и мнимой «полуосями» гиперболы.
- действительной и мнимой «полуосями» гиперболы.
4°. Найдем точки пересечения гиперболы с прямой 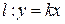 .
.
Для этого решим систему 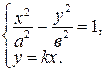
Получаем уравнение  . Корни
. Корни  - это абсциссы точки пересечения прямой
- это абсциссы точки пересечения прямой 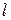 с
с 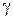 . Рассмотрим три случая:
. Рассмотрим три случая:
1) Если 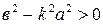 , т.е.
, т.е. 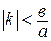 , то
, то 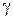 и
и 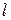 имеют две общие точки;
имеют две общие точки;
2) Если  , т.е.
, т.е. 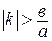 , то
, то 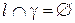 ;
;
3) 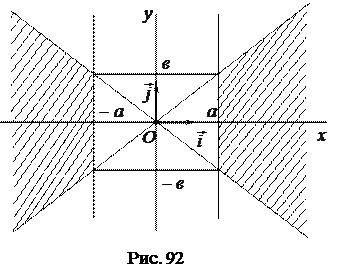 Если
Если 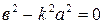 , т.е.
, т.е.  , то
, то 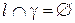 .
.
Следовательно, все точки гиперболы расположены в заштрихованных областях (рис. 92). Гипербола имеет две ветви.
Случаю 3) соответствуют две прямые 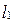 и
и 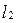 с угловыми коэффи-
с угловыми коэффи-
циентами 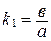 и
и 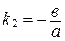 . Эти прямые (
. Эти прямые ( и
и 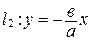 ) называются асимптотами гиперболы.
) называются асимптотами гиперболы.
При неограниченном возрастании абсолютной величины абсциссы точки 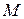 гиперболы точка
гиперболы точка 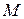 неограниченно приближается к асимптоте.
неограниченно приближается к асимптоте.
 Учитывая свойства 1°- 4°, построим изображение гиперболы (рис. 93):
Учитывая свойства 1°- 4°, построим изображение гиперболы (рис. 93):
Число 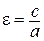 называется эксцентриситетом гиперболы. Так как для гиперболы
называется эксцентриситетом гиперболы. Так как для гиперболы 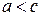 , то
, то 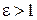 . Чем больше
. Чем больше 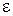 , тем больше гипербола «вытянута» вдоль мнимой оси.
, тем больше гипербола «вытянута» вдоль мнимой оси.
Гипербола, у которой 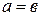 , называется равносторонней. Ее каноническое уравнение
, называется равносторонней. Ее каноническое уравнение 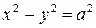 . Уравнения ее асимптот
. Уравнения ее асимптот 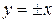 .
.
Директрисами эллипса называются две прямые, параллельные мнимой оси и отстоящие от нее на расстоянии 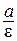 .
.
Уравнения директрис:
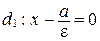 или
или 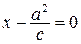 ;
;
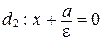 или
или 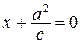 (рис. 94).
(рис. 94).
Гипербола обладает следующим директориальным свойством: для любой точки 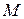 , принадлежащей гиперболе, отношение расстояния от
, принадлежащей гиперболе, отношение расстояния от 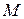 до фокуса к расстоянию от
до фокуса к расстоянию от 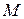 до соответствующей директрисы равно эксцентриситету, т.е.
до соответствующей директрисы равно эксцентриситету, т.е.
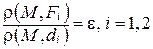 (рис. 94).
(рис. 94).
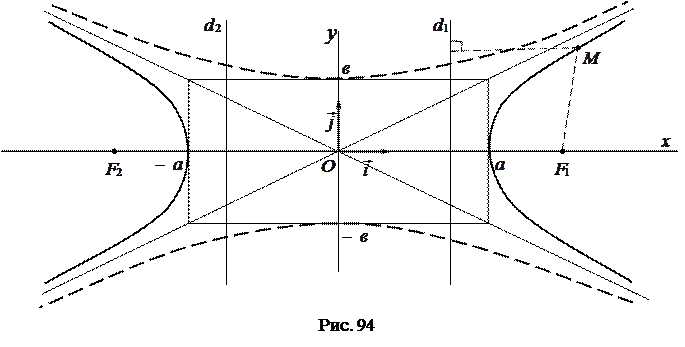
Замечание 1. Директрисы гиперболы не имеют общих точек с гиперболой.
Гипербола 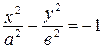 называется сопряженной к гиперболе
называется сопряженной к гиперболе 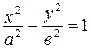 . Ее мнимой осью является ось
. Ее мнимой осью является ось 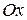 (на рис. 94 она изображена пунктиром).
(на рис. 94 она изображена пунктиром).
Date: 2015-07-11; view: 602; Нарушение авторских прав