Утверждение 1.2. Система линейных алгебраических уравнений имеет бесчисленное множество решений, если ранг совместной системы меньше числа неизвестных

На практике процедуру исследования систем линейных алгебраических уравнений проводят следующим образом.

Пусть система уравнений задается соотношением (1.4). Дальнейшие исследования проводят с расширенной матрицей системы:

.

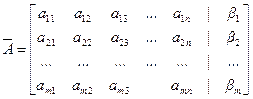Очевидно, что в данном случае имеет место соотношение 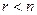. Такая матрица с помощью гауссовых исключений сводится к ступенчатому виду.

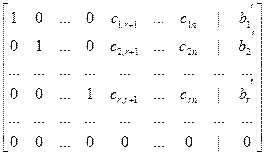
Тогда соответствующая эквивалентная система будет представлена в виде:

(

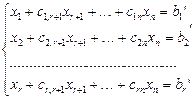В таком случае задача исследования системы состоит в том, чтобы описать ее общее решение. Для этого необходимо базисные переменные выразить через свободные. Итак, имеем

(

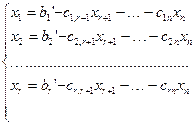Последнее соотношение и определяет общее решение системы. Положив свободные сменные равными нулю, 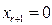, , 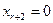…, 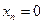и вычислив значения базисных переменных, получают одно из частных решений исследуемой системы

; ; …; ,

, , …, .

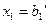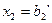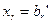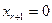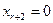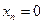Непосредственно процесс исследования системы проиллюстрируем на примере.

Задача1.9. Выполнить общее исследование системы линейных алгебраических уравнений

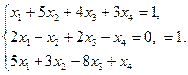
Решение

1. Выпишем расширенную матрицу системы и выполним соответствующие гауссовые исключения.

.

.

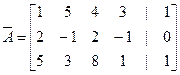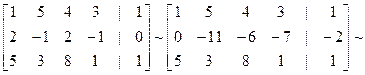
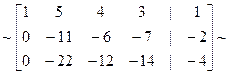
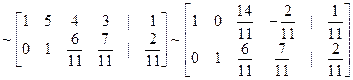2. На основании анализа матрицы

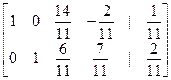
получим:

а);. Таким образом, и исходная система совместная;

б);. Итак, исходная система будет иметь бесчисленное множество решений, и ее исследование будет состоять в том, чтобы описать это множество;

в) исходная система имеет две 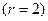базисные переменные и две 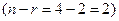свободные переменные.

3. На основании матрицы

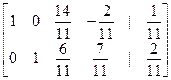
можно записать систему, эквивалентную исходной:

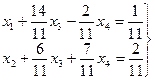
Очевидно, что за базисные переменные следует принять переменные 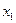и 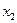, а свободными будут переменные 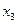и .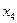

4. Опишем общее решение исходной системы

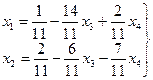
5. Проверку правильности найденного решения выполним по одному из базисных уравнений системы, например, по первому:

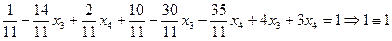
Итак, общее решение системы найдено верно.

6. Опишем некоторую совокупность частных решений. Для этого свободным переменным 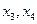предоставим некоторые числовые значения и вычислим значения базисных переменных 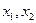Результаты внесем в таблицу.

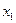
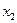
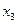
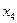
1/11	2/11
-3/11	-4/11
-1

Date: 2015-07-10; view: 566; Нарушение авторских прав