Эквивалентность матриц

Определение 1.17. Две матрицы 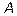и 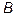называются эквивалентными, если их ранги равны, т.е. .

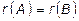Если матрицы 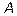и 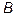эквивалентны, то это обозначается так: ~ .

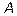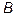Теорема 1.5. Ранг матрицы не меняется при элементарных преобразованиях.

То есть элементарные преобразования – это такие преобразования, которые не приводят к изменению ранга матрицы. К ним относятся:

– транспонирование матрицы,

– перестановка параллельных рядов;

– вычеркивание ряда, все элементы которого равны нулю;

– умножение всех элементов какого-либо ряда на число, отличное от нуля;

– добавление к элементам какого-либо ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число .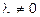

Следствие теоремы 1.5. Если матрица 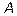получена из матрицы 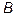при помощи конечного числа элементарных преобразований, то матрицы 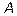и 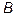эквивалентны.

При вычислении ранга матрицы ее следует привести при помощи конечного числа элементарных преобразований к трапециевидной форме или к эквивалентной единичной матрице.

Определение 1.18. Трапециевидной будем называть такую форму представления матрицы, когда в окаймляющем миноре наибольшего порядка, отличном от нуля, все элементы, стоящие ниже диагональных, равны нулю.

Например:

.

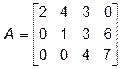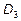
Здесь 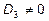, элементы матрицы 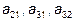обращаются в нуль. Тогда форма представления такой матрицы будет трапециевидной.

Как правило, матрицы к трапециевидной форме приводят при помощи алгоритма Гаусса. Идея алгоритма Гаусса состоит в том, что, умножая элементы первой строки матрицы на соответствующие множители, добиваются, чтобы все элементы первого столбца, расположенные ниже элемента 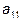, обратились в нуль. Затем, умножая элементы второго столбца на соответствующие множители, добиваются, чтобы все элементы второго столбца, расположенные ниже элемента 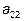, обратились в нуль. Далее аналогично.

Задача 1.5. Определить ранг матрицы с помощью элементарных преобразований

.

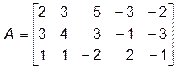Для удобства применения алгоритма Гаусса поменяем местами первую и третью строки

~ ~ ~

~ ~ ~ .

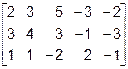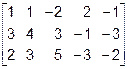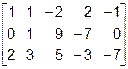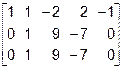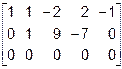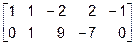Очевидно, что здесь 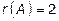. Однако, для приведения результата к более изящному виду можно далее продолжить преобразования над столбцами:

~ ~ ~ ~

~ ~ ~ ~ .

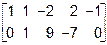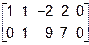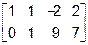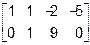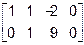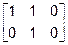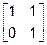Тема 1.2. Системы линейных алгебраических уравнений (СЛАУ)

Система m линейных алгебраических уравнений с n неизвестными имеет вид:

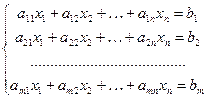(1.2)

Совокупность чисел 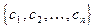, которые, будучи подставленными в систему (1.2) вместо неизвестных, обращают все уравнения СЛАУ в числовые тождества, называется решением системы.

Если система (1.2) имеет хотя бы одно решение, она называется совместной, в противном случае – несовместной.

Совместная система может обладать либо единственным решением, либо бесчисленным множеством решений.

Пусть А - матрица коэффициентов системы, 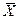- вектор- столбец неизвестных, 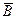- вектор-столбец свободных членов. Тогда в матричном виде система запишется в виде

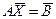
Если количество уравнений m равно количеству неизвестных n, система имеет квадратную матрицу А порядка n. Определитель называется определителем системы.

Date: 2015-07-10; view: 1759; Нарушение авторских прав