Метод приведенного градиента

Зададимся вопросом: что, если забыть, что базис не орто­нормальный, и при вычислении проекции антиградиента -g вместо р =-C(C^TC)^-1C^Tg брать просто p* = -CC^Tg? К чему приведет такая ошибка? Понятно, что р* вычислить просто. Не нужно даже вычислять произведение матриц СС^Т, а про­сто сначала вычислить C^Tg, а потом умножить С на резуль­тат. Достаточно хранить только базисные векторы.

Но имеет ли смысл такое упрощение сложной формулы Для вычисления проекции р? При неортонормальном базисе это упрощение не будет давать проекцию. Это оче­видно. Тем не менее рассмотрим какой вектор р мы полу­чили бы.

Во-первых, это допустимое направление, так как вектор представлен в виде Су*, где у* =-C^Tg это вектор коэффи­циентов разложения р* по базисным векторам.

Во-вторых, и это самое интересное, р это подходящее направление, т.е. направление уменьшения целевой функ­ции, так как скалярное произведение р на антиградиент по­ложительно. Действительно,

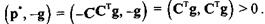
Вектор CC^Tg, где g градиент, называется приведенный градиент, а р* можно было бы назвать приведенный анти­градиент.

Важно отметить, что при таком построении дополни­тельных базисных векторов имеется возможность исклю­чать не одно, а сразу несколько ограничений из активного набора. Если принять меры по предотвращению «зигза­гов», это открывает возможность быстрее выйти на нужную грань, т.е. сформировать нужный набор активных ограничений, ускорить сходимость и сократить время счета.

Вопросы для самоконтроля:

1.Метод наискорейшего подъема и спуска (для задач без ограничений)

2.Метод проекции градиента.

3.Метод условного градиента. Условные методы Ньютона.

Рекомендуемая литература:

1.Измаилов А.Ф., Солодов М.В. Численные методы оптимизации. М.: Физматлит, 2003.

2.Банди Б. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988.

Date: 2015-07-10; view: 823; Нарушение авторских прав