
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лекция 3. Различные формы задач линейного программирования
|
|
Содержание лекционного занятия:
· Стандартная форма задачи линейного программирования
· Каноническая форма задачи линейного программирования (ЗЛП)
· Переход от стандартной формы задачам линейного программирования (ЗЛП) к канонической
Рассмотренные выше примеры задач линейного программирования укладываются в общий класс задач линейного программирования. Однако записи целевых функций и главным образом ограничений в них существенно различаются. В первом примере искомые переменные зависят от одного индекса и ограничения имеют вид неравенств; в другом примере искомые переменные зависят от двух индексов, а ограничения имеют вид равенств. Существует также ряд практических задач, в которых часть ограничений представлена в виде равенств, а часть — в виде неравенств.
Различают три основные формы задачи линейного программирования, к которым может быть сведена любая содержательная постановка задачи.
Общая форма задачи линейного программирования
Задана система m линейных уравнений с n переменными:
 (1)
(1)
xj >0, где(j = l...n), (2)
а линейная функция:
F = c1 x1 +с2 x2+с3 x3+... + cn xn → max(min). (3)
Необходимо найти такой вектор Х=(х1, х2,х3,.. xn), который удовлетворяет ограничениям (1) и (2) и при котором линейная функции F принимает максимальное (или минимальное) значение.
Как видно из представленной выше записи, в общей форме задачи линейного программирования система ограничений (1) включает в себя как равенства, так и неравенства, а целевая функция может стремиться как к максимуму, так и к минимуму.
Более кратко задачу линейного программирования в общей форме можно представить в следующем виде:
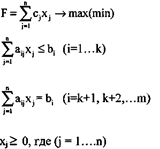
Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение Х*=(х*1,х*2...хn), удовлетворяющее системам ограничений, при которой линейная функция F достигает оптимального значение (минимума или максимума).
Термины «решение» или «план» — синонимы, однако первый используется чаще, когда речь идет о формализованной постановке задачи, а второй — о содержательной.
Date: 2015-07-10; view: 582; Нарушение авторских прав