
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Навигация
|
|
Теорема Нётер
Https://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E5%EC%E0_%CD%B8%F2%E5%F0
[править | править вики-текст]
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Теоре́ма Эмми Нётер утверждает, что каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения:
однородности времени соответствует закон сохранения энергии,
однородности пространства соответствует закон сохранения импульса,
изотропии пространства соответствует закон сохранения момента импульса,
калибровочной симметрии соответствует закон сохранения электрического заряда и т. д.
Теорема обычно формулируется для систем, обладающих функционалом действия, и выражает собой инвариантность лагранжиана по отношению к некоторой непрерывной группе преобразований.
Теорема установлена в работах учёных гёттингенской школы Д. Гильберта, Ф. Клейна и Э. Нётер. В наиболее распространенной формулировке была доказана Эмми Нётер в 1918 году.
Содержание
[убрать]
- 1 Формулировка
- 1.1 Классическая механика
- 1.2 Теория поля
- 1.3 Дифференциальные уравнения
- 1.3.1 Законы сохранения
- 1.3.2 Вариационные симметрии
- 1.3.3 Характеристики векторных полей
- 1.3.4 Теорема Нётер
- 2 Законы сохранения
- 3 Приложения
- 4 Примечания
- 5 Литература
- 6 Ссылки
Формулировка[править | править вики-текст]
Классическая механика[править | править вики-текст]
Каждой однопараметрической группе диффеоморфизмов 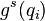 , сохраняющих функцию Лагранжа, соответствует первый интеграл системы, равный
, сохраняющих функцию Лагранжа, соответствует первый интеграл системы, равный
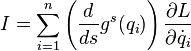
В терминах инфинитезимальных преобразований, пусть инфинитезимальное преобразование координат имеет вид
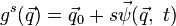
и функция Лагранжа 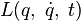 инвариантна относительно этих преобразований, то есть
инвариантна относительно этих преобразований, то есть
 при
при 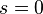
Тогда у системы существует первый интеграл, равный
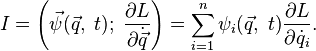
Теорему можно обобщить на случай преобразований, затрагивающих также и время, если представить её движение как зависящее от некоторого параметра 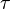 , причем в процессе движения
, причем в процессе движения 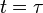 . Тогда из преобразований
. Тогда из преобразований
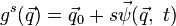
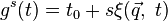
следует первый интеграл
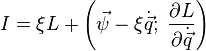
Теория поля[править | править вики-текст]
Теорема Нётер допускает прямое обобщение на случаи систем с бесконечным числом степеней свободы, примером которых являются гравитационное и электромагнитное поле. А именно, пусть функция Лагранжа системы зависит от  потенциалов, зависящих, в свою очередь, от
потенциалов, зависящих, в свою очередь, от 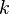 координат. Функционал действия будет иметь вид
координат. Функционал действия будет иметь вид
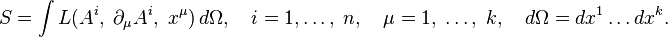
Пусть однопараметрическая группа 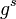 диффеоморфизмов пространства потенциалов сохраняет функцию Лагранжа, тогда сохраняется вектор
диффеоморфизмов пространства потенциалов сохраняет функцию Лагранжа, тогда сохраняется вектор
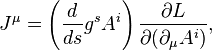
называемый вектором потока Нётер. По повторяющимся индексам подразумевается суммирование, 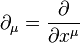 . Смысл сохранения вектора потока Нётер в том, что
. Смысл сохранения вектора потока Нётер в том, что
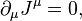
поэтому поток 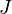 через любую замкнутую поверхность в пространстве координат равен 0. В частности, если выделить среди координат одну, называемую временем, и рассмотреть гиперплоскости постоянного времени, то поток
через любую замкнутую поверхность в пространстве координат равен 0. В частности, если выделить среди координат одну, называемую временем, и рассмотреть гиперплоскости постоянного времени, то поток 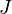 через такую гиперплоскость постоянен во времени, при условии достаточно быстрого спадения поля на бесконечности и некомпактности гиперповерхности, чтобы поток вектора через боковую границу области пространства между двумя гиперповерхностями был равен 0. В классической теории поля таким свойством обладает, например, тензор энергии-импульса для электромагнитного поля. В вакууме лагранжиан поля не зависит явно от координат, поэтому имеется сохраняющаяся величина, ассоциируемая с потоком энергии-импульса.
через такую гиперплоскость постоянен во времени, при условии достаточно быстрого спадения поля на бесконечности и некомпактности гиперповерхности, чтобы поток вектора через боковую границу области пространства между двумя гиперповерхностями был равен 0. В классической теории поля таким свойством обладает, например, тензор энергии-импульса для электромагнитного поля. В вакууме лагранжиан поля не зависит явно от координат, поэтому имеется сохраняющаяся величина, ассоциируемая с потоком энергии-импульса.
Дифференциальные уравнения[править | править вики-текст]
Пусть имеется вариационная задача с функционалом действия 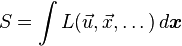 . Здесь
. Здесь 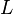 — лагранжиан,
— лагранжиан,  — независимые переменные,
— независимые переменные, 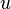 — зависимые переменные, то есть функции от
— зависимые переменные, то есть функции от  .
. 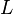 может зависеть также и от производных
может зависеть также и от производных 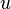 по
по  , не обязательно только первого порядка.
, не обязательно только первого порядка.
Вариационная задача для такого функционала приводит к дифференциальным уравнениям Эйлера-Лагранжа, которые можно записать в виде
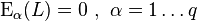 ,
,
где 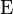 — операторы Эйлера-Лагранжа:
— операторы Эйлера-Лагранжа:
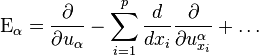 ,
,
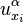 — производная функции
— производная функции 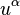 по переменной
по переменной  . Многоточие означает, что если
. Многоточие означает, что если 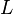 зависит от производных порядка выше первого, то нужно добавить соответствующие слагаемые в
зависит от производных порядка выше первого, то нужно добавить соответствующие слагаемые в 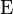 . В компактной записи
. В компактной записи 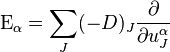 , где
, где 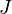 — мультииндекс. Суммирование ведётся по всем слагаемым таким, что производная
— мультииндекс. Суммирование ведётся по всем слагаемым таким, что производная 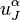 входит в
входит в 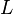 .
.
Теорема Нётер связывает так называемые вариационные симметрии функционала 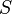 с законами сохранения, выполняющимися на решениях уравнений Эйлера-Лагранжа.
с законами сохранения, выполняющимися на решениях уравнений Эйлера-Лагранжа.
Законы сохранения[править | править вики-текст]
Закон сохранения для системы дифференциальных уравнений — это выражение вида
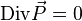
которое справедливо на решениях этой системы, то есть такое, что если подставить в него эти дифференциальные уравнения, получится тождество. В данном случае рассматриваются дифференциальные уравнения Эйлера-Лагранжа. Здесь 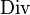 — полная дивергенция (дивергенция с полными производными) по
— полная дивергенция (дивергенция с полными производными) по  .
. 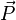 — гладкие функции
— гладкие функции 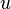 ,
,  и производных
и производных 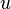 по
по  .
.
Тривиальными законами сохранения называются законы сохранения
- для которых
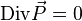 само по себе является тождеством без учёта каких-либо дифференциальных уравнений;
само по себе является тождеством без учёта каких-либо дифференциальных уравнений; - или для которых
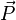 обращается в 0 сразу при подстановке дифференциальных уравнений, без вычисления дивергенции (сохраняется тождественный ноль на решениях);
обращается в 0 сразу при подстановке дифференциальных уравнений, без вычисления дивергенции (сохраняется тождественный ноль на решениях); - или для которых
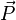 есть линейная комбинация предыдущих типов.
есть линейная комбинация предыдущих типов.
Если для двух законов сохранения с функциями 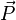 и
и 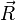 разность
разность 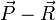 даёт тривиальный закон сохранения, такие два закона сохранения называются эквивалентными.
даёт тривиальный закон сохранения, такие два закона сохранения называются эквивалентными.
Всякий закон сохранения эквивалентен закону сохранения в характеристической форме — то есть такому, для которого
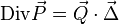 ,
,
где 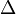 — выражения, которые входят в определение системы дифференциальных уравнений:
— выражения, которые входят в определение системы дифференциальных уравнений: 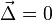 . Для описываемого случая
. Для описываемого случая 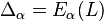 и
и
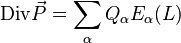 .
.
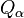 зависят от
зависят от 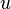 ,
,  и производных
и производных 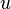 по
по  и называются характеристиками закона сохранения.
и называются характеристиками закона сохранения.
Вариационные симметрии[править | править вики-текст]
Пусть имеется обобщённое векторное поле
 .
.
«Обобщённое» понимается в том смысле, что 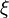 и
и 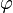 могут зависеть не только от
могут зависеть не только от 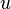 и
и  , но и от производных
, но и от производных 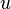 по
по  .
.
Определение: 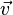 называется вариационной симметрией функционала
называется вариационной симметрией функционала 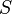 , если существует набор функций
, если существует набор функций 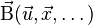 такой, что
такой, что
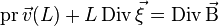 .
.
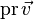 — продолжение
— продолжение 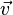 . Продолжение учитывает, что действие
. Продолжение учитывает, что действие 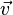 на
на 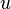 и
и  вызывает также инфинетизимальное изменение производных, и задаётся формулами
вызывает также инфинетизимальное изменение производных, и задаётся формулами
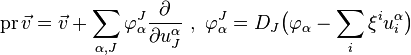 .
.
В формуле для продолжения необходимо брать, кроме 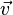 , слагаемые с такими
, слагаемые с такими 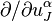 , для которых
, для которых 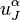 входят в
входят в 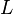 или, в общем случае, в то выражение, на которое продолжение действует.
или, в общем случае, в то выражение, на которое продолжение действует.
Смысл определения вариационной симметрии состоит в том, что 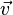 — это инфенитизимальные преобразования, которые в первом порядке меняют функционал
— это инфенитизимальные преобразования, которые в первом порядке меняют функционал 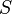 таким образом, что уравнения Эйлера-Лагранжа преобразуются в эквивалентные. Справедлива
таким образом, что уравнения Эйлера-Лагранжа преобразуются в эквивалентные. Справедлива
теорема: если 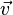 является вариационной симметрией, то
является вариационной симметрией, то 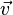 является (обобщённой) симметрией уравнений Эйлера-Лагранжа:
является (обобщённой) симметрией уравнений Эйлера-Лагранжа:
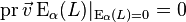 .
.
Эта формула означает, что инфинетезимальные изменения выражений  , записанные здесь в виде
, записанные здесь в виде 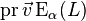 , обращаются в 0 на решениях.
, обращаются в 0 на решениях.
Характеристики векторных полей[править | править вики-текст]
Набор функций 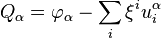 (в обозначениях, данных выше) называется характеристикой векторного поля
(в обозначениях, данных выше) называется характеристикой векторного поля 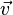 . Вместо
. Вместо 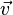 можно брать векторное поле
можно брать векторное поле
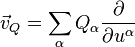 ,
,
которое называется эволюционным представителем 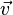 .
.
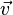 и
и 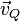 определяют по сути одну и ту же симметрию, поэтому, если известны характеристики
определяют по сути одну и ту же симметрию, поэтому, если известны характеристики 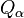 , можно считать, что тем самым задана и симметрия. Продолжение
, можно считать, что тем самым задана и симметрия. Продолжение 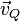 определяется аналогично продолжению
определяется аналогично продолжению 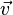 , но формально проще, поскольку не нужно отдельно учитывать вклад от
, но формально проще, поскольку не нужно отдельно учитывать вклад от 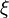 .
.
Теорема Нётер устанавливает связь между характеристиками законов сохранения и характеристиками векторных полей.
Теорема Нётер[править | править вики-текст]
Обобщённое векторное поле 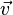 определяет группу симметрий функционала
определяет группу симметрий функционала 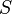 в том и только в том случае, если его характеристика
в том и только в том случае, если его характеристика 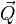 является характеристикой закона сохранения
является характеристикой закона сохранения 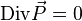 для соответствующих уравнений Эйлера-Лагранжа.
для соответствующих уравнений Эйлера-Лагранжа.
Законы сохранения[править | править вики-текст]
В классической механике законы сохранения энергии, импульса и момента импульса выводятся из однородности/изотропности лагранжиана системы — лагранжиан (функция Лагранжа) не меняется со временем сам по себе и не изменяется переносом или поворотом системы в пространстве. По сути это означает то, что при рассмотрении некой замкнутой в лаборатории системы будут получены одни и те же результаты — вне зависимости от расположения лаборатории и времени проведения эксперимента. Другие симметрии лагранжиана системы, если они есть, соответствуют другим сохраняющимся в данной системе величинам (интегралам движения); например, симметрия лагранжиана гравитационной и кулоновской задачи двух тел приводит к сохранению не только энергии, импульса и момента импульса, но и вектора Лапласа — Рунге — Ленца.
Приложения[править | править вики-текст]
Теорема Нётер позволяет получать значительную информацию о свойствах решений системы дифференциальных уравнений, основываясь лишь на их симметрии. Она также является одним из методов интегрирования обыкновенных дифференциальных уравнений, так как позволяет в некоторых случаях находить первые интегралы системы уравнений и таким образом понижать число неизвестных функций. Например:
- Сохранение импульса системы следует из её инвариантности относительно пространственных сдвигов. Конкретнее, если сдвиг вдоль оси X не меняет систему уравнений, то сохраняется импульс
 вдоль этой оси.
вдоль этой оси. - Сохранение момента импульса следует из инвариантности системы относительно вращений пространства.
- Закон сохранения энергии — это следствие однородности времени, позволяющей произвольным образом сдвигать начало отсчёта времени.
В случае уравнений в частных производных необходимо, вообще говоря, искать бесконечное число первых интегралов. Даже зная их, обычно нелегко выписать общее решение.
В силу своей фундаментальности, теорема Нётер используется в таких областях физики, как квантовая механика, для самого введения понятий импульса, момента импульса и т. д. Инвариантность уравнений относительно некоторых симметрий становится единственной сутью этих величин и гарантирует их сохранение.
В квантовой теории поля аналогом теоремы Нётер являются тождества Уорда — Такахаси (англ.), позволяющие получить дополнительные законы сохранения. Например, закон сохранения электрического заряда следует из инвариантности физической системы относительно изменения фазы комплексной волновой функции частицы и соответствующей калибровки векторного и скалярного потенциала электромагнитного поля.
Заряд Нётер также используется для вычисления энтропии стационарной чёрной дыры[1].
Примечания[править | править вики-текст]
- ↑ Calculating the entropy of stationary black holes. (англ.)
Литература[править | править вики-текст]
- Арнольд В. И. Математические методы классической механики, изд. 5-ое, — М.: Едиториал УРСС, 2003, ISBN 5-354-00341-5
- Ибрагимов Н. Х. Группы преобразований в математической физике. — М.: Наука, 280 с., 1983 г.
Ссылки[править | править вики-текст]
- Перевод статьи Нётер на английский
- Статья о Теореме Нётер, by John Baez (англ.)
- E. Noether’s Discovery of the Deep Connection Between Symmetries and Conservation Laws by Nina Byers
- Теорема Нётер на MathPages. (англ.)
- Symmetric energy-momentum tensor in Maxwell, Yang-Mills, and Proca theories obtained using only Noether’s theorem. (англ.)
- Giachetta G., Mangiarotti L., Sardanashvily G. On the notion of gauge symmetries of generic Lagrangian field theory. — J. Math. Phys. 50 (2009) 012903; arXiv 0807.3003.
<img src="//ru.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;" />
Источник — «http://ru.wikipedia.org/w/index.php?title=Теорема_Нётер&oldid=64022133»
Категории:
- Теоретическая механика
- Теория поля
- Квантовая теория поля
- Физические теоремы
- Законы сохранения
- Симметрия (физика)
- Дифференциальные уравнения
Навигация
Date: 2015-07-02; view: 906; Нарушение авторских прав