
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 1. Теоретические основы темы «Теорема Менелая и теорема Чевы »
|
|
«Все незначительное нужно,
чтобы значительному быть…»
И. Северянин.
1.1. Теорема Чевы.
Мы знаем, что медианы треугольника пересекаются в одной точке, биссектрисы треугольника пересекаются в одной точке, высоты треугольника (или их продолжения) пересекаются в одной точке. Поставим теперь общий вопрос. Рассмотрим  ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки A
ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки A 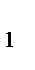 ,B
,B 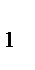 и C
и C 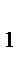 (рис.1).
(рис.1).
При каком расположении этих точек прямые AA 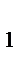 , BB
, BB 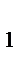 и CC
и CC  пересекутся в одной точке?
пересекутся в одной точке?
Ответ на этот вопрос нашел в 1678 году итальянский инженер-гидравлик Джованни Чева (1698г.-1734г.). Чева создал учение о секущих, положившее начало новой синтетической геометрии. Известна его работа «О взаимном расположении пересекающихся прямых» (1678г.) и теорема Чевы о соотношениях отрезков в треугольнике.
(Отрезки, соединяющие вершины треугольника с точками на противолежащих сторонах, называют чевианами - понятно, почему).
Сформулируем теорему Чевы.
Теорема. Пусть в  ABC на сторонах BC,AC и AB или их продолжениях взяты соответственно точки A
ABC на сторонах BC,AC и AB или их продолжениях взяты соответственно точки A  ,B
,B 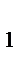 и C
и C 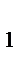 , не совпадающие с вершинами треугольника. Прямые AA
, не совпадающие с вершинами треугольника. Прямые AA 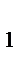 , CC
, CC 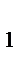 и BB
и BB 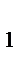 пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство
пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство

 .
. 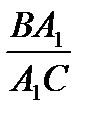 .
. 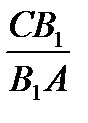 =1 (
=1 ( )
)
Доказательство. Следует заметить, что формулировка теоремы Чевы содержит два взаимно обратных утверждения.
Необходимость. Пусть AA 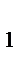 , BB
, BB 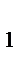 , CC
, CC 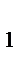 пересекаются в точке O. Докажем справедливость равенства (
пересекаются в точке O. Докажем справедливость равенства ( ).
).
1) Рассмотрим сначала случай внутренней точки O (рис.1а), при котором точки A 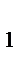 ,B
,B 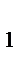 ,C
,C  лежат на отрезках BC,AC и AB соответственно.
лежат на отрезках BC,AC и AB соответственно.
Проведем через вершину B прямую a ll AC (рис.2). Пусть AA 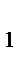 ∩ a =M,
∩ a =M,
 CC
CC  ∩ a= N.
∩ a= N.
Замечаем, что  AA
AA 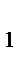 C~
C~  MA
MA 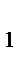 B по I признаку (
B по I признаку (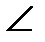 AA
AA 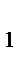 C=
C= 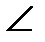 MA
MA 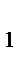 B как вертикальные,
B как вертикальные, 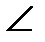 CAA
CAA 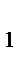 =
= 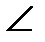 BMA
BMA 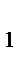 как накрест лежащие при параллельных прямых а, АС и секущей АМ).
как накрест лежащие при параллельных прямых а, АС и секущей АМ).
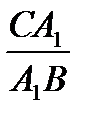 =
= 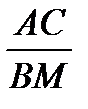 (1).
(1).
Аналогично
из подобия  AC
AC 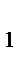 C и
C и  BC
BC 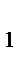 N по I признаку имеем
N по I признаку имеем 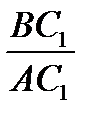 =
= 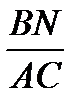 (2);
(2);
 AOB
AOB 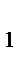 ~
~  MOB
MOB 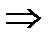
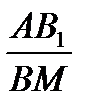 =
= 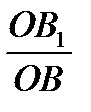 (3)
(3)
 B
B 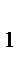 OC~
OC~  BON
BON 
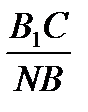 =
=  (4)
(4)
Из (3) и (4) получаем  =
= 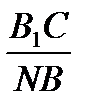 или
или 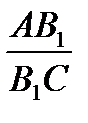 =
= 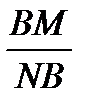 (5)
(5)
Перемножив соответственно левые и правые части равенств (1), (2) и (5), получим равенство( ):
):
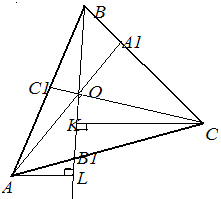
 .
. 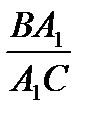 .
. 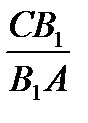 =
= 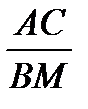 .
. 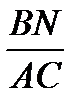 .
. 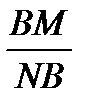 =1. Необходимость доказана.
=1. Необходимость доказана.
Примечание 1: равенство ( ) можно получить, заменив отношения отрезков в его левой части на отношение площадей. Считаю целесообразным привести другое
) можно получить, заменив отношения отрезков в его левой части на отношение площадей. Считаю целесообразным привести другое
доказательство.
Итак, вернемся к (рис.1а), заметим, что  AOB и
AOB и  COB
COB
рис.3 имеют общую сторону BO.
Их высоты AL и CK соответственно (рис.3).  AB
AB 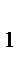 L~
L~  CB
CB 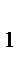 K,
K,  =
= 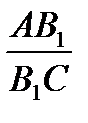 .
.
Тогда 
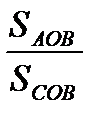 =
= 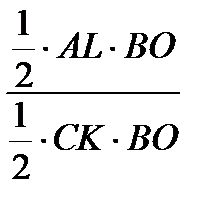 =
= 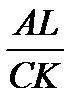 =
= 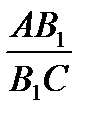 .
.
Аналогично,  AOC и
AOC и  COB имеют общую сторону OC.
COB имеют общую сторону OC.

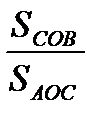 =
=  . Наконец,
. Наконец,  =
= 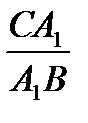 .
.
Перемножая эти три равенства, получаем 1= 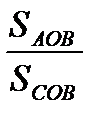 .
. 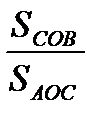 .
.  =
= 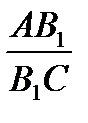 .
. 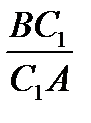 .
.  ,что соответствует (
,что соответствует ( ) [19,с.87].
) [19,с.87].
2) Рассуждая аналогично для случая внешней точки O (рис1б), замечаем, что теорема Чевы остается справедливой для точек A  ,B
,B 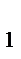 ,C
,C 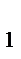 , одна из которых принадлежит стороне треугольника, а две другие – продолжениям сторон. Действительно, пусть AL -высота в
, одна из которых принадлежит стороне треугольника, а две другие – продолжениям сторон. Действительно, пусть AL -высота в  AOB,проведенная из вершины A, CK- высота в
AOB,проведенная из вершины A, CK- высота в  COB, проведенная из вершины C, OB – их общая сторона (рис.4).
COB, проведенная из вершины C, OB – их общая сторона (рис.4).
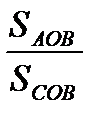 =
=  . Из подобия
. Из подобия  AB
AB  L и
L и  СB
СB 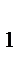 K по I признаку имеем
K по I признаку имеем 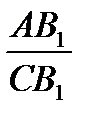 =
= 
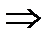
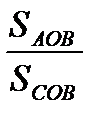 =
= 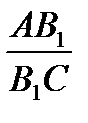 . Аналогично,
. Аналогично, 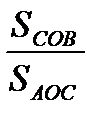 =
=  ,
,  =
= 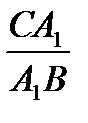 . Перемножая, получаем нужное равенство. Следует только помнить, что при составлении отношений, выходя из вершины треугольника, мы сначала идем в точку деления(A
. Перемножая, получаем нужное равенство. Следует только помнить, что при составлении отношений, выходя из вершины треугольника, мы сначала идем в точку деления(A 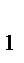 ,B
,B  или C
или C  соответственно) - она может быть расположена вне стороны треугольника - а потом к очередной вершине; заканчивать необходимо в той же вершине, с которой начали.
соответственно) - она может быть расположена вне стороны треугольника - а потом к очередной вершине; заканчивать необходимо в той же вершине, с которой начали.
Примечание 2: можно сообщить теорему Чевы учащимся уже в 8 классе (общеобразовательный класс, факультатив, кружок) после изучения темы «Площадь треугольника». Тогда доказательство можно провести следующим образом.
Так как  ABB
ABB 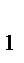 и
и  B
B 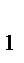 BC (рис.1а) имеют равные высоты, то их площади относятся как основания, то есть
BC (рис.1а) имеют равные высоты, то их площади относятся как основания, то есть 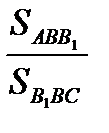 =
= 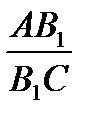
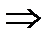 S
S 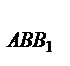 =
= 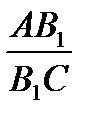 .S
.S 
Аналогично,  =
= 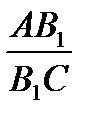
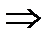 S
S 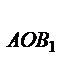 =
= 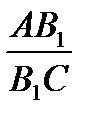 .S
.S 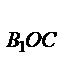
Тогда 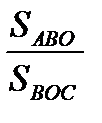 =
= 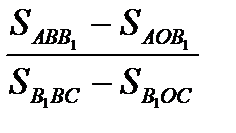 =
= 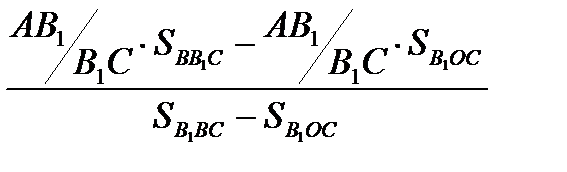 =
= 
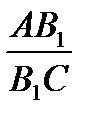 (1)
(1)  =
= 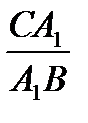 (высоты равны)
(высоты равны) 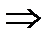 S
S 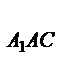 =
= 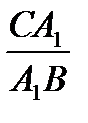 .S
.S 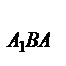
C другой стороны, 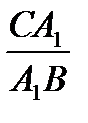 =
= 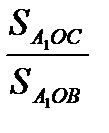
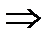 S
S 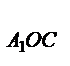 =
= 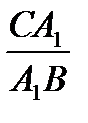 .S
.S 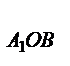

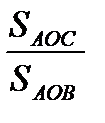 =
= 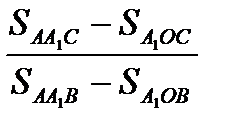
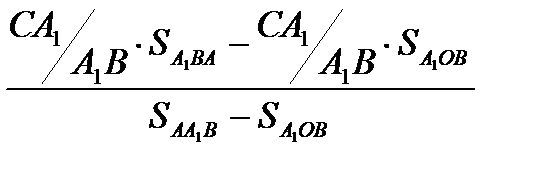 =
= 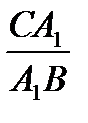 (2) И, наконец,
(2) И, наконец, 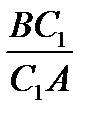 =
= 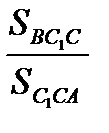 =
= 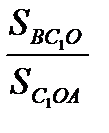 , откуда выражаем S
, откуда выражаем S 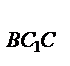 и S
и S 
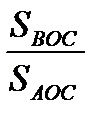 =
= 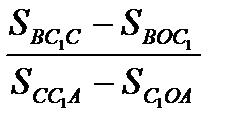 =
= 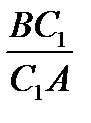 (3). Перемножим (1), (2), (3), получим равенство (
(3). Перемножим (1), (2), (3), получим равенство ( ).
).
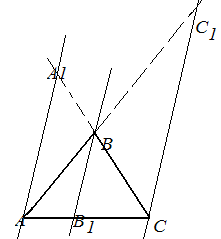 3) Докажем равенство (
3) Докажем равенство ( ) для случая, когда прямые AA
) для случая, когда прямые AA 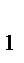 ,BB
,BB 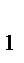 ,CC
,CC 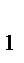 параллельны
параллельны
(рис.5)
а)  CAA
CAA 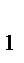 ~
~  CB
CB 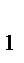 B по I признаку,
B по I признаку, 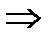
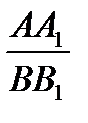 =
=  =
= 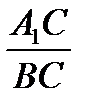 (1)
(1)
б)  BB
BB 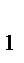 A~
A~  C
C 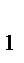 CA по I признаку,
CA по I признаку, 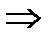
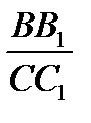 =
= 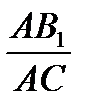 =
= 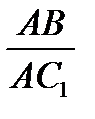 (2)
(2)
в)  С
С 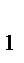 BC~
BC~  ABA
ABA 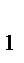 по I признаку,
по I признаку, 
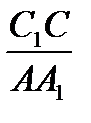 =
= 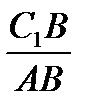 =
= 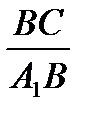 (3)
(3)
Перемножая равенства 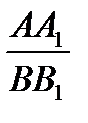 =
=  ,
, 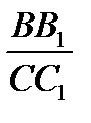 =
= 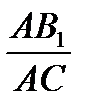 и
и 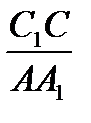 =
= 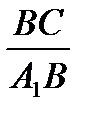 ,
,
рис.5 получаем 1= 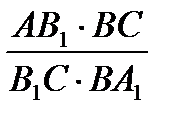
 BC=
BC=  (4)
(4)
Перемножая равенства 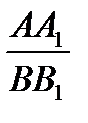 =
= 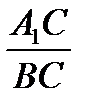 ,
, 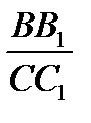 =
= 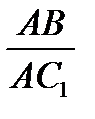 и
и 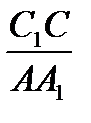 =
= 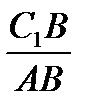 , получаем
, получаем
1= 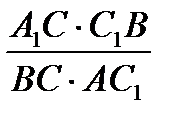
 BC=
BC= 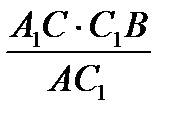 (5). Из (4) и (5)
(5). Из (4) и (5)  =
= 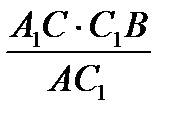 , поделим его на
, поделим его на
правую часть, получим ( ).
).
Достаточность.
Пусть для точек A 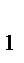 ,B
,B  ,C
,C  выполнено равенство (
выполнено равенство ( ).Покажем, что прямые
).Покажем, что прямые
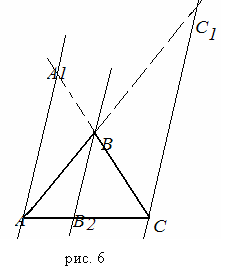 AA
AA  ,BB
,BB  и CC
и CC  проходят через одну точку. Пусть AA
проходят через одну точку. Пусть AA 
 BB
BB  =O, CO
=O, CO  AB=C
AB=C 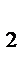 .Тогда для точек A
.Тогда для точек A 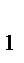 ,B
,B  ,C
,C 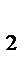 по теореме Чевы (необходимость) выполняется условие
по теореме Чевы (необходимость) выполняется условие  .
. 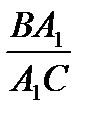 .
. 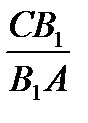 =1.
=1.
Сравнивая это равенство со ( ), получаем, что
), получаем, что  =
= 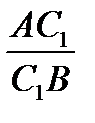 . Это означает, что точки C
. Это означает, что точки C  и C
и C 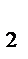 делят отрезок AB (в случае внутренней точки O) в одном и том же отношении, а значит, точка C
делят отрезок AB (в случае внутренней точки O) в одном и том же отношении, а значит, точка C  совпадает с точкой C
совпадает с точкой C 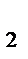 . В случае внешней точки O рассуждение аналогично. Если же (
. В случае внешней точки O рассуждение аналогично. Если же ( ) выполняется и при этом AA
) выполняется и при этом AA  ll CC
ll CC  , то через вершину B проведем прямую b ll AA
, то через вершину B проведем прямую b ll AA  , найдем точку B
, найдем точку B 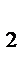 ее пересечения с прямой AC (рис. 6).
ее пересечения с прямой AC (рис. 6).
Так как для случая трёх параллельных прямых теорема Чевы (прямое утверждение) была доказана, то для прямых AA  ,b,CC
,b,CC  выполняется
выполняется 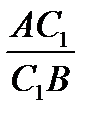 .
. 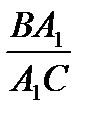 .
. 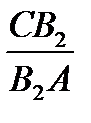 =1.
=1.
Сравнивая его со ( ), получаем
), получаем 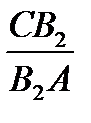 =
= 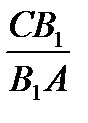 . Если точки B
. Если точки B  и B
и B  принадлежат отрезку AC, то они делят его в одном и том же отношении, а значит, совпадают. Если B
принадлежат отрезку AC, то они делят его в одном и том же отношении, а значит, совпадают. Если B  и B
и B  не принадлежат отрезку AC, то они лежат по одну сторону от точек A или C в зависимости от того, лежит ли A
не принадлежат отрезку AC, то они лежат по одну сторону от точек A или C в зависимости от того, лежит ли A  на отрезке AC или C
на отрезке AC или C  на отрезке AB, и из равенства отношений следует совпадение точек B
на отрезке AB, и из равенства отношений следует совпадение точек B  и B
и B  ,а значит, BB
,а значит, BB  ll AA
ll AA  ll СС
ll СС  . Теорема доказана.
. Теорема доказана.
Примечание 3: процедура составления( ) не зависит от выбора «отправной» вершины и направления обхода, так как всегда будет получаться произведение, равное 1. Действительно, если
) не зависит от выбора «отправной» вершины и направления обхода, так как всегда будет получаться произведение, равное 1. Действительно, если  .
. 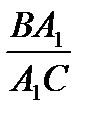 .
. 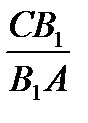 =m=1, то
=m=1, то 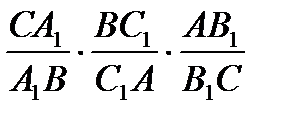 =
= 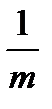 =1 (и т.д.).
=1 (и т.д.).
Date: 2015-07-02; view: 1706; Нарушение авторских прав