Разные задачи

Попробуйте решить эти задачи с помощью теоремы Менелая.

1. Диагонали выпуклого четырехугольника ABCD пересекаются в точке Q. Через

точку Q проведена прямая, пересекающая стороны AB и CD в точках K и L

соответственно. Найти отношение DL:LC, если известно, что AK=KB,

BQ:QD=2:3, CQ:QA=3:4.

2.Диагонали выпуклого четырехугольника KLMN пересекаются в точке Q. Через

точку Q проведена прямая, пересекающая стороны KL и MN в точках A и B

соответственно. Найти отношение MQ:QN, если известно, что KA:BM=5:6,

LQ:QK=3:2, NB:AL=4:1.[2, с.61] (в указанной литературе приводится другой

способ решения).

3. Биссектриса угла A треугольника ABC делит медиану, проведенную из

вершины B, в отношении 5:4, считая от вершины B. В каком отношении,

считая от вершины C, эта биссектриса делит медиану, проведенную из

вершины C?

4. На стороне AC треугольника ABC выбрана точка B 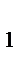, а на стороне AB – точка

C 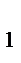так, что 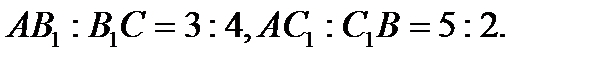В каком отношении, считая от вершин

треугольника, точка пересечения отрезков BB 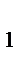и CC делит каждый из этих

отрезков?[24, с.189]

5. В тетраэдре ABCD через середины K и N ребер AD и BC проведена плоскость,

пересекающая ребра AB и CD соответственно в точках M и L. Площадь

четырехугольника KLMN равна 16, а 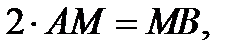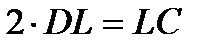. Вычислите

расстояние от вершины A до плоскости KLNM, если объем многогранника

NACLK равен 40.

6. В тетраэдре KLMN проведено сечение плоскостью. Точки A,B,C,D

принадлежат плоскости и ребрам KN,LN,LM и KM соответственно, причем

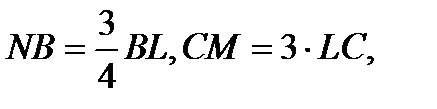
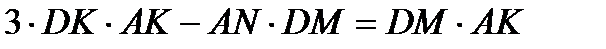и . Найти

отношение объемов частей, на которые плоскость ABCD делит тетраэдр.

7. В пирамиде ABCD проведено сечение KMLN так, что точка K лежит на ребре

AD, точка M – на ребре DC, точка N – на ребре AB, точка L - -на ребре BC, и O-

точка пересечения диагоналей KL и MN четырехугольника KMLN. Сечение

KMLN делит пирамиду на две части. Найти отношение объемов этих частей,

если известны следующие соотношения между длинами отрезков:

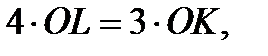
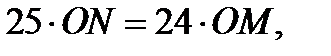
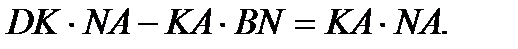[19, с.464]

Date: 2015-07-02; view: 1065; Нарушение авторских прав