в предположении, что пробегает целые значения

.

Равенство 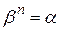запишется в виде

.

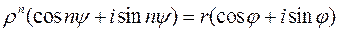Приравнивая модули и аргументы (с учетом многозначности), получим, что последнее равенство равносильно равенствам

Следовательно, модуль искомого числа равен арифметическому корню из 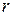степени 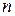, 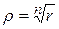. Аргумент находится по правилу

Таким образом, корни n -й степени из комплексного числа существуют и все они даются формулой

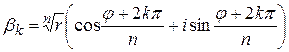
при любом 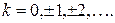Ввиду периодичности функций косинус и синус различные значения 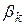получаются только при 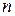последовательных значениях величины 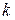, в частности при 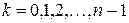. Таким образом, справедлив следующий результат.

Теорема:Существует ровно значений корня -й степени из комплексного числа. Их дает формула

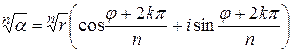
в предположении, что пробегает целые значения.

Заметим, что из правил вычисления корня 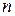-й степени следует, что все 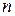значений корня изображаются точками комплексной плоскости, которые находятся на окружности радиуса 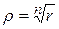с центром в начале координат и делят эту окружность на 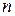равных частей.

Пример 4.Найдем все значения . Запишем данное число в тригонометрической форме,

.

Согласно формуле,

.

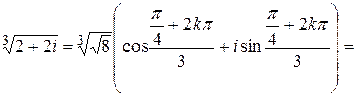
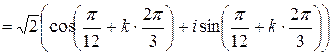Для 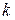достаточно взять значения 0, 1, 2. Получим три значения:

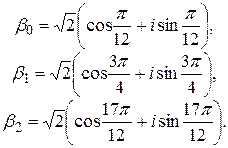
Date: 2015-07-02; view: 401; Нарушение авторских прав