Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Комплексные числа. В курсе математического анализа обычно употребляются только действительные числа и действительные функции с действительными аргументами
|
|
В курсе математического анализа обычно употребляются только действительные числа и действительные функции с действительными аргументами. Однако, некоторые операции (например, извлечение корня четной степени из отрицательного числа, решение квадратного уравнения) не могут быть выполнены в области действительных чисел и приводят к комплексным числам.
Рассмотрим основные положения алгебры комплексных чисел.
1. Число вида z = x + i y, где i2 = -1, называется комплексным числом, x – действительная часть, y – мнимая часть. Их обозначают так x = Re z, y = Im z. Если x = 0, то число z = 0 + iy называют чисто мнимым. Если y = 0, то получается действительное число z = x + 0y.
2. 
z = x – i y – сопряженное комплексное число.
3. Модулем комплексного числа называется действительное число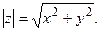 
4. Два комплексных числа считаются равными z1 = z2, если x1 = x2, y1 = y2.
5. z = x + i y = 0 только, если x = 0, y = 0.
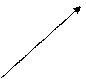
Известно, что действительные числа изображаются точками числовой оси. Комплексное число z = z + i y изображается точкой (х, у) комплексной плоскости.
y
А z = x + i y
ρ
Y
φ
O x x
 |
Геометрическим образом комплексного числа является также вектор ОА.
Если ввести полярные координаты, то x = ρ cos φ, y = ρ sin φ и z = ρ(cos φ + i sin φ). Здесь
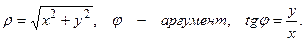
Над комплексными числами вводятся действия сложения, вычитания, умножения и деления.
1. Сложение (вычитание):
z1 ± z2 = (x1 + i y1) ± (x2 + i y2) = x1 ± x2 + i (y1 ± y2).
2. Умножение (осуществляется по обычным правилам алгебры).
(x1 + i y1) (x2 + i y2) = x1x2 – y1y2 + i (x1y2 + y1x2), i2 = -1, i3 = i i2 =− i, i4 = i2 i2 = 1.
Рассмотрим произведение двух комплексных чисел в тригонометрической форме.
Распространяя это правило на любое число сомножителей и, считая их равными, получим формулу возведения комплексного числа в целую положительную степень (формулу Муавра).
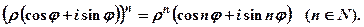
3. Деление. Частным двух комплексных чисел z1 и z2 называется комплексное число
z = z1/z2, удовлетворяющее условию z z2 = z1.
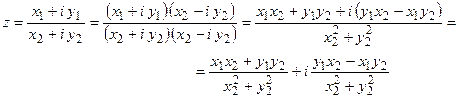
B тригонометрической форме
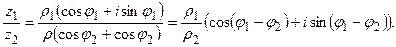
Для проверки следует умножить делитель на частное.
Date: 2015-07-02; view: 432; Нарушение авторских прав