Если в разложении найден комплексный корень, то в этом разложении есть корень комплексно сопряжённый к найденному

Теорема. Для любого многочлена ненулевой степени в поле комплексных чисел справедливо разложение на множители: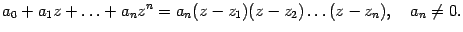

Пример. Решить уравнение x⁴ – 4 = 0.

Решение: Левая часть этого уравнения – многочлен f(x)=x⁴ – 1. Основная теорема алгебры утверждает, что этот многочлен может быть разложен на 4 линейных множителя, именно

f(x) = (x + 1)(x – 1)(x + i)(x – i).

Подставим полученное разложение в данное уравнение: (x + 1)(x – 1)(x + i)(x – i) = 0. Теперь, приравнивая к нулю каждый из сомножителей, получим четыре корня данного уравнения:

x + 1 = 0, x₁ = – 1; x – 1 = 0, x₂ = 1; x + i = 0, x₃ = – i; x – i = 0, x₄ = i.

Таким образом, данное уравнение имеет четыре корня, ровно столько, какова его степень.

Пример. Рассмотрим уравнение х²+с=0, где 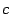- вещественное положительное число.

Решение: Легко проверить, что его корни х₁= 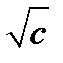i, x₂=- 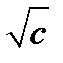i, где 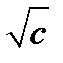- обычный арифметический корень.

Пример. Решим уравнение ax²+bx+c=0, где a,b,c - вещественные числа, , .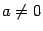

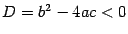Решение: Для этого выделим в правой части полный квадрат: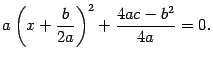

Откуда 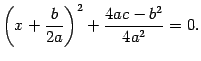Поэтому то есть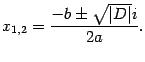

Итак, если дискриминант 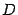отрицательный, то корни уравнения находятся по формулам: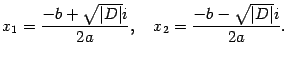

Пример. Решите уравнение x²+2x+5=0.

Решение: Находим дискриминант: D=4-20= -16

Находим корни: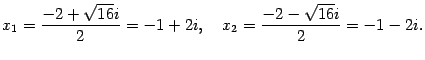

Пример. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющие корень z₁=-1-2i.

Решение: Второй корень z₂ уравнения является числом, сопряженным с данным корнем z_1, то есть z₂=-1+2i. По теореме Виета находим P=-(z₁+z₂)=2, q=z₁z₂=5. Ответ z^2-2z+5=0.

Пример. Решите уравнение .

Решение: Находим дискриминант: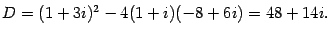

Решим уравнение y²=D. Для этого находим 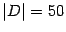. Пусть 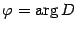. Тогда 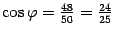. Достаточно найти только одно решение. Второе получим умножением его на (-1). 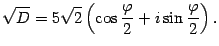По формулам половинного аргумента с учетом того, что 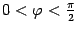, получим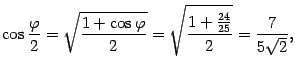

Таким образом, .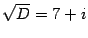

По формулам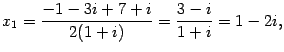

Date: 2015-07-02; view: 828; Нарушение авторских прав