Формула Муавра

Для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если ₁, ₂,..., _n – аргументы чисел z₁, z₂,..., z_n, то

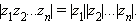
В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.

Найдем квадрат комплексного числа z = r(cos + i sin ), т.е. результат произведения этого числа на само себя: z² = z∙z = r(cos 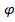+ i sin 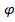)∙r(cos 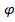+ i sin 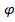) = r²(cos 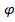+ i sin 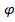)² = r²(cos 2 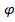+ i sin 2 ).

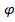Повторяя n раз операцию возведения в степень числа z, мы получим формулу n-ой степени числа z:

zⁿ = rⁿ(cos n 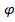+ i sin n 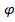),где n – натуральное число.

Методом математической индукции можно доказать эту формулу. Она представляет собой обобщение формулы, открытой Муавром. Муавр открыл ее для случая, когда модуль комплексного числа z равен 1. Формула Муавра имеет вид:(cos + i sin )ⁿ = cos n + i sin n , где n N.

С помощью формулы Муавра можно вывести многие полезные соотношения, в частности, между тригонометрическими выражениями.

Формула Муавра позволяет найти значения корней любой (n-й) степени в поле комплексных чисел.

Под корнем n-й степени из числа z понимают такое число a, n-я степень которого равна z: aⁿ = z.

Первая формула Муавра: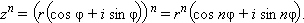

Пример. Вычислить z⁴, если z = 1- 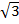i.

Решение: 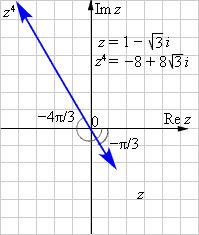Как было найдено в примере п.2. §3, данное число в тригонометрической форме имеет вид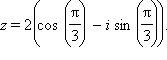

По первой формуле Муавра получаем:

Число z называется корнем степени n, n 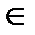N из комплексного числа w, если zⁿ = w. Корень степени n обозначается z= 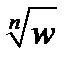. Пусть теперь число w фиксировано. Найдём z из уравнения zⁿ = w.

Если w = 0, то у уравнения zⁿ=0существует единственное решение z = 0.

Если w ≠ 0, то положим, что нам известно тригонометрическое представление числа w = r₀(cos ₀ + i sin ₀), и будем искать число z также в тригонометрической форме: z = r(cos 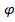+ i sin 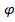). Из определения аргумента и геометрической интерпретации комплексных чисел следует, что два комплексных числа, записанных в тригонометрической форме, равны тогда и только тогда, когда равны их модули, а аргументы отличаются на угол, кратный 2π. Имеем: zⁿ = w, rⁿ(cos n 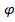+ i sin n 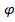)= r₀(cos ₀ + i sin ₀), где откуда получается:

Итак, все решения уравнения zⁿ = w задаются формулой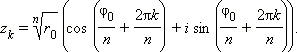

Заметим, что если в эту формулу подставлять натуральные числа k, то при k = 0, 1,..., n-1 мы будем получать разные комплексные числа, а при k = n имеем: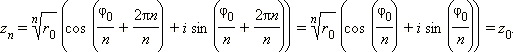

Значит, и в дальнейшем значения корней будут повторяться. Следовательно, существует ровно n корней уравнения zⁿ = w и все они задаются одной формулой.

Вторая формула Муавра: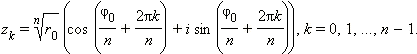

Пример. Найти .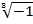

Решение: Представим число –1 в тригонометрической форме: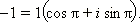

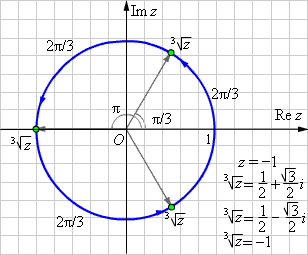
По второй формуле Муавра получаем: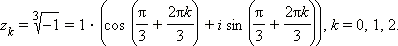

Получаем последовательно:

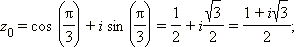
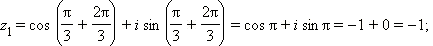
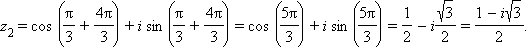
Date: 2015-07-02; view: 9544; Нарушение авторских прав