Основная теорема алгебры

Изученные сведения о комплексных числах позволяют рассмотреть вопрос о решении алгебраических уравнений в поле комплексных чисел. Напомним, что алгебраическим уравнением называют уравнение вида: a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 +... + a₁x + a₀ = 0.

Левая часть его представляет собой некоторый многочлен f(x), где x – неизвестное, a_n, a_n-1 ,... a₁ , a₀ – коэффициенты (действительные или комплексные числа), n – натуральное число. Если a_n 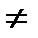0, то мы имеем дело с уравнением n-ой степени, т.е. степень уравнения совпадает с высшей степенью неизвестного.

Корнем (или решением) уравнения f(x) = 0 называется такое число t, при подстановке которого вместо неизвестного в данное уравнение мы получаем верное числовое равенство: f(x) = 0.

Нам известно, что каждое уравнение первой степени ax + b = 0 (a 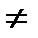0) имеет решение .

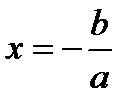Нам также известно, что каждое квадратное уравнение ax² + bx + c = 0 имеет два решения:

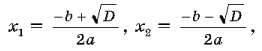где D = b² – 4ac – дискриминант квадратного уравнения.

Правда, если D = 0, то эти решения совпадают.

В 1799 г. немецкому математику Гауссу удалось доказать теорему о том, что всякое алгебраическое уравнение с действительными и даже комплексными коэффициентами имеет по крайней мере один комплексный корень. Теорема Гаусса позволила доказать основную теорему алгебры: всякий многочлен n-й степени может быть разложен на n линейных множителей, откуда непосредственно следует, что всякое алгебраическое уравнение n-й степени имеет n корней.

Date: 2015-07-02; view: 1114; Нарушение авторских прав