Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Операции над комплексными числами и их свойства
|
|
С учётом замечательного соотношения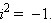 
легко получаются формулы сложения и умножения для комплексных чисел. Пусть заданы два комплексных числа z1 = a + bi и z2 = c + di.
1) Сравнение. z1 = z2 или a + bi = c + di означает, что a = c и b = d
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
2) Сложение. z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i
· Коммутативность сложения: z1 + z2 = z2 + z1 для любых z1 , z2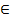 
С.
Док-во: По определению сложения получаем
z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i,
z2 + z1 = (c + di) + (a + bi) = (c + a) + (d + b)i = (a + c) + (b + d)i = z1 + z2.
так как с + a = a + с, d + b = b + d, т. е. для любых действительных чисел выполняется переместительное (коммутативное) свойство сложения.▄
· Ассоциативность сложения: (z1 + z2) + z3 = z1 + (z2 + z3) для любых z1 , z2 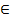С.
· 
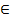Существует такое число z = 0, которое обладает свойством z + 0 = z, для любого z С.
3) Вычитание.
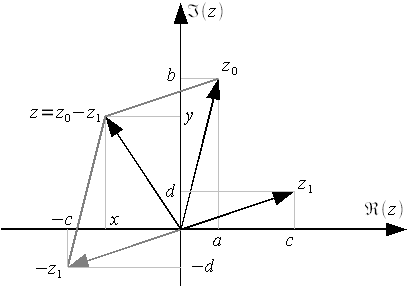
Для любых двух чисел z1 и z2 существует такое число z, что z1+ z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.
z1 - z2 = (a + bi) − (c + di) = (a − c) + (b − d)i
4) Умножение.
Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства 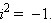, то и перемножать эти числа можно как многочлены.
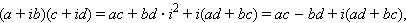
· Коммутативность умножения: z1 z2 = z2 z1 для любых z1 , z2 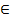С.
Док-во: z1 z2 = (a + bi)(c + di) = aс + adi + bci + bdi2 = (ac - bd) + (ad + bc)i,
z2 z1 = (c + di) (a + bi) = сa + cbi + dai + dbi2 = (ca - db) + (cb + da)i = (ac - bd) + (ad + bc)i = z1 z2,
поскольку для любых действительных чисел ac = ca, bd = db, т. е. выполняется переместительное (коммутативное) свойство умножения.▄
· Ассоциативность умножения: (z1 z2)z3 = z1(z2z3) для любых z1 , z2, z3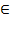 
С.
· Дистрибутивность сложения относительно умножения: z1(z2 + z3) = z1 z2 + z1z3 для любых z1 , z2, z3 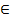С.
· Для любого комплексного числа z: z · 1 = z
5) Деление.
Для любых двух чисел z1 и z2 существует такое число z, что z1∙ z = z2. Такое число z называется частным двух комплексных чисел и обозначается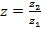 
. Деление на 0 невозможно.
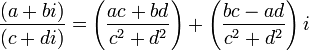
Пример. Вычислить z1 + z2 и z1z2, где z1 = 1 + 2i и z2 = 2 – i.
Решение:
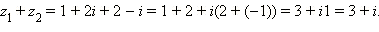
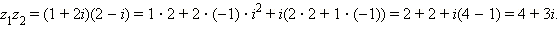
Пример. Пусть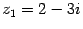 
, 
.
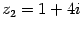Решение: Тогда:
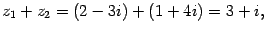
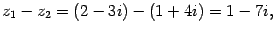
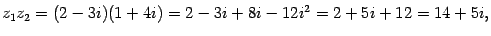
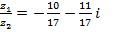
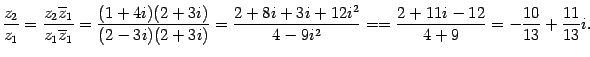
Пример. Вычислить 
.
Решение: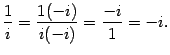 
Если число z = a + bi, то число 
= a - bi называется комплексно сопряжённым с числом z.
Комплексно сопряжённое число обозначается . Для этого числа справедливы соотношения:
1) 
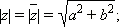
2) 
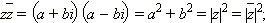
3) 
4) сумма и произведение двух комплексных сопряженных чисел есть числа действительные.
5) 
(сопряжённое к сопряжённому есть исходное).
6) 
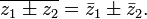
7) 
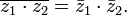
8) 
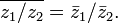
Пример. Найдите число, сопряжённое к комплексному числу (1 + 2i)(3 – 4i).
Решение: Имеем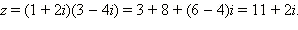 
Следовательно,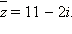 
Пример. Вычислите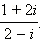 
Решение: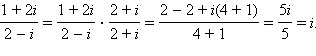 
Приведем классификацию комплексных чисел:
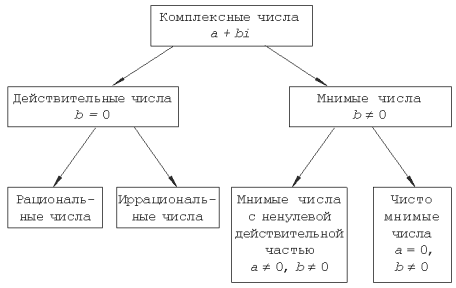
Date: 2015-07-02; view: 847; Нарушение авторских прав