Представление комплексных чисел

П.1. АЛГЕБРАИЧЕСКАЯ ФОРМА.

Запись комплексного числа 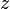в виде z = a + bi, называется алгебраической формой комплексного числа. Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ):

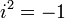1) Сложение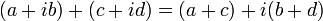

2) Умножение

3) Деление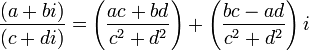

П.2. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА.

Часто бывает удобна немного другая форма записи комплексного числа. Пусть 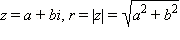и = arg z. Тогда по определению аргумента имеем: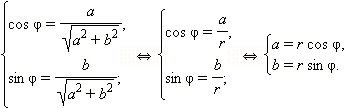

Отсюда получается

z = a + bi = (домножим и разделим на 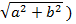= 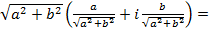r (cos + i sin ).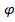

Такая форма называется тригонометрической формой записи комплексного числа.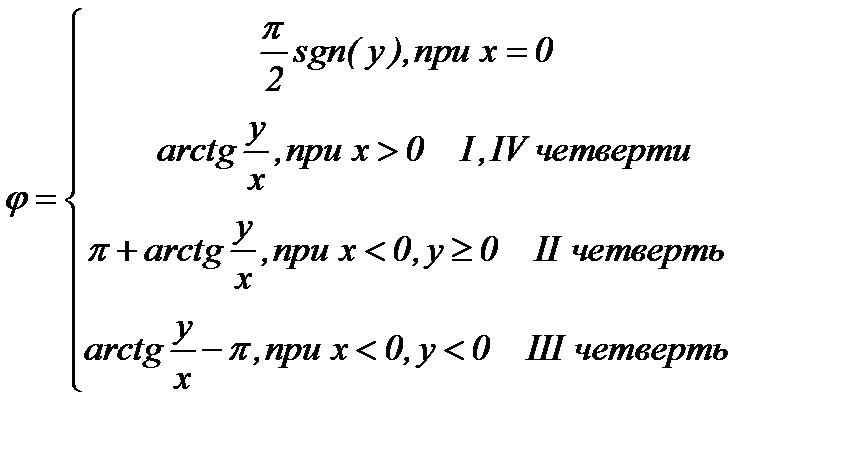

Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Замечание: При записи числа в тригонометрической форме НЕЛЬЗЯ вычислять значения cos и sin 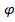, иначе мы потеряем явное указание аргумента 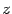и снова вернемся к алгебраической форме.

Кроме того, если угол получился отрицательным, то знак "- " НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса.

Пример. Записать число 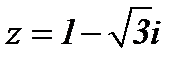в тригонометрической форме.

Решение: Найдём модуль этого числа: 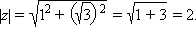Аргумент данного числа находится из системы 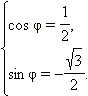Значит, один из аргументов числа 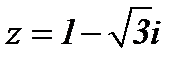равен .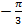

Получаем: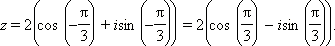

Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z₁ = r₁(cos ₁ + i sin ₁) и z₂ = r₂(cos ₂ + i sin 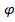₂). Имеем:

1) Умножение: при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

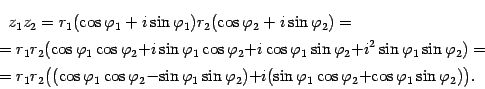
Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому

Последняя запись является тригонометрической формой комплексного числа z₁ z₂. Значит,

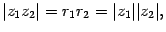
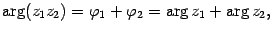
2) Деление: при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.

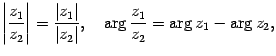
3) если 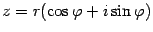, то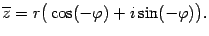

П.3. ПОКАЗАТЕЛЬНАЯ ФОРМА.

Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой 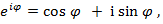которая носит название формулы Эйлера.

Пусть комплексное число 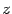в тригонометрической форме имеет вид z = r (cos + i sin 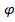). На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим .

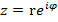Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь = r, = arg z.

Арифметические действия над комплексными числами, записанными в показательной форме, производятся следующим образом.

1) Умножение: при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

2) Деление: при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.

Пример. Пусть z=-1+i. Напишите показательную форму числа .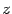

Решение: Находим модуль и аргумент числа: = r = 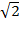, II четверть = arg z = arctg(-1)+π = .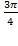

Следовательно, показательная форма комплексного числа такова: .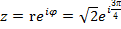

Пример. Комплексное число записано в показательной форме .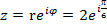

Найдите его алгебраическую форму.

Решение: По формуле Эйлера

С помощью формулы Эйлера можно определить показательную функцию комплексного аргумента. Пусть z = a + bi. Тогда 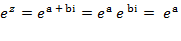(cosb + i sinb).

Например,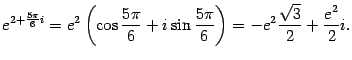

Заменим в формуле Эйлера на 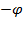. Получим: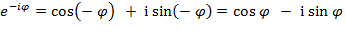

Сложив последнюю формулу с формулой Эйлера, получим: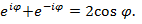

Откуда 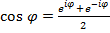. Аналогично, с помощью вычитания, .

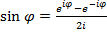Пример. Вычислить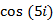

Решение: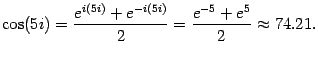

Таким образом, в комплексной области модуль косинуса может быть и больше 1.

Date: 2015-07-02; view: 1129; Нарушение авторских прав