Понятие комплексного числа

К мплексные числа

Комплексные числа, как впрочем и отрицательные, возникли из внутренней потребности самой математики, конкретнее – из практики и теории решения алгебраических уравнений. С комплексными числами впервые математики встретились при решении квадратных уравнений. Вплоть до ХVI века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание.

П.1. ОСНОВНЫЕ ПОНЯТИЯ.

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Символ 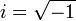предложил Эйлер, взявший для этого первую букву слова лат. imaginarius.

Комплексные числа часто обозначают одной буквой, например, z = a + ib или z = х + уi.

Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z.

Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.

Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел: арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами.

(Действительно, 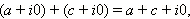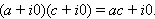). Следовательно, комплексные числа вида z = a + i · 0 отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными.

Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается С, т.е. .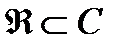

В отличие от действительных чисел, числа вида z = 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает свойством: 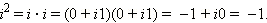Таким образом,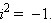

Замечания:

1) Ошибочно определение числа i как единственного числа, удовлетворяющего уравнению x² = − 1, так как число (− i) также удовлетворяет этому уравнению.

2) Часто используемое выражение 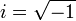не вполне корректно, так как алгебраический корень определяется над множеством неотрицательных чисел.

Матричная модель: Комплексные числа можно также определить как семейство вещественных матриц вида 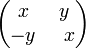с обычным матричным сложением и умножением.

Действительной единице будет соответствовать 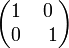, мнимой единице —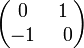

а) iⁿ = 1, если n делится на 4;
б) iⁿ = i, если при делении n на 4 в остатке получаем 1;
в) iⁿ = – 1, если при делении n на 4 в остатке получаем 2;
г) iⁿ = – i, если при делении n на 4 в остатке получаем 3.

П.2. КОМПЛЕКСНАЯ ПЛОСКОСТЬ.

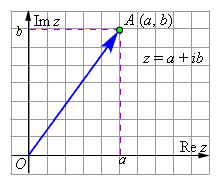
Геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.

Очень важной является интерпретация комплексного числа z = a + ib как вектора 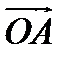с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Любому комплексному числу z = a + ib соответствует вектор 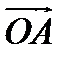(a,b) и наоборот, каждому вектору 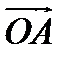(a,b) соответствует, и притом единственное, число z = a + ib.

Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости.

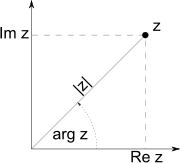Модулем комплексного числа называется длина вектора, соответствующего этому числу: 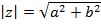. Модуль комплексного числа z обычно обозначается или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора.

Если z = a + i0, то 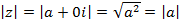, то есть для действительного числа модуль совпадает с абсолютной величиной.

Ясно, что 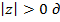ля всех z ≠ 0.

Некоторые свойства модуля:

1) 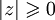, причём 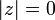тогда и только тогда, когда z = 0 + i0=0.

2) 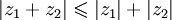(неравенство треугольника)

3)

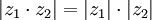
4)

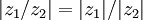
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором . Величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае. Аргумент комплексного числа z имеет бесконечное множество значений, отличающихся друг от друга на число, кратное 2π.

Угол , аргумент комплексного числа, обозначается = arg z. Для числа z = 0 аргумент не определён. Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет. Действительно, если = arg z – аргумент этого комплексного числа, то все числа вида + 2πn также будут аргументами этого комплексного числа. Наименьшее по абсолютной величине значение аргумента называется главным. Argz=argz+2πn.

Например, аргументами комплексного числа z = 1 + i являются углы 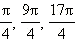и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π.

Заданием только лишь своего модуля определяется только комплексное число z = 0.

Из определения тригонометрических функций следует, что = arg z тогда и только тогда, когда для этого выполняется система 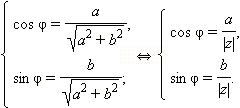или .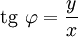

Пример. Найти модуль и аргумент комплексного числа z = –1 – i.

Решение: Так как Re z = –1 и Im z = –1, то точка z лежит в третьей координатной четверти.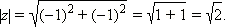

Для поиска аргумента решим систему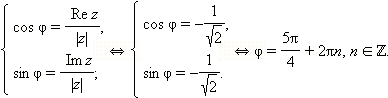

Date: 2015-07-02; view: 729; Нарушение авторских прав