
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Операции над комплексными числами в тригонометрической форме. Пусть z1 =r1⋅(cos j1+i⋅sin j1), z2 =r2⋅(cos j2+i⋅sin j2)
|
|
Пусть z1 =r1⋅(cos j1+i⋅sin j1), z2 =r2⋅(cos j2+i⋅sin j2).
1. Умножение z1z2= r1 r2⋅(cos j1+i⋅sin j1)⋅(cos j2+i⋅sin j2)=
=r1r2 ((cos j1 ⋅cos j2 –sinj1 ⋅sinj2 ) + i(sin j1⋅cosj2 + sin j2 ⋅cos j1)) =
=r1r2 (cos(j1 +j2)+i⋅sin (j1 +j2 )).
Таким образом, z1z2 = r1r2 (cos(j1 +j2)+i⋅sin (j1 +j2 )), т.е. при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
2. Деление. Пусть z1 =r1⋅(cos j1+i⋅sin j1), z2 =r2⋅(cos j2+i⋅sin j2), причем z2¹0.
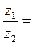
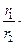
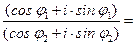
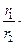
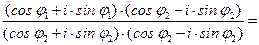

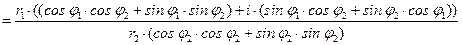
= 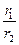 (cos(j1 -j2)+i⋅sin (j1 -j2 ))
(cos(j1 -j2)+i⋅sin (j1 -j2 ))
Таким образом, 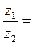
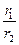 (cos(j1 -j2)+i⋅sin (j1 -j2 )), т.е. при делении комплексных чисел в тригонометрической форме, их модули делятся друг на друга, а аргументы вычитаются.
(cos(j1 -j2)+i⋅sin (j1 -j2 )), т.е. при делении комплексных чисел в тригонометрической форме, их модули делятся друг на друга, а аргументы вычитаются.
3. Возведение в степень. Пусть z = r⋅(cos j+i⋅sin j) Тогда, по правилу умножения комплексных чисел, z2=z⋅z=r2(сos2j+i⋅sin2j) и т. д. Методом математической индукции можно доказать, что
zn=rn (cos nj+i⋅sin nj), n ∈ℕ, (3)
т.е. при возведении комплексного числа в натуральную степень n, его модуль возводится в степень n, а аргумент умножается на n.
Определение 4. Корнем n-й степени из комплексного числа z называется такое комплексное число u, что un = z, и обозначается 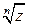 = u .
= u .
4. Извлечение корня n -й степени из комплексного числа z = r⋅(cos j+i⋅sin j), z  .
.
Будем искать u в тригонометрической форме, т.е. u=r0(cos j0+i⋅sinj0) такое, что un = z, т.е. (r0(cos j0+i⋅sinj0)) n = r⋅(cos j+i⋅sin j). Согласно правилу возведения в степень, получим r0n(cos nj0+i⋅sin nj0)= r⋅(cos j+i⋅sin j).
Так как равные комплексные числа изображаются одной и той же точкой на плоскости, то из рисунка и определений 1 и 2 следует, что их модули должны быть равны, а аргументы могут отличаться лишь на 2p k, k ∈ℤ.
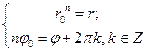 , следовательно,
, следовательно, 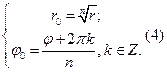
При k=0 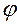 01 =
01 = 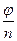
При k=1 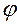 02 =
02 = 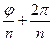
При k =2 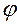 03 =
03 = 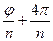
***
При k = n -1 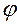 0 ( n-1) =
0 ( n-1) = 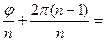
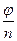 +2
+2 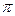 -
- 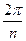
При k = n 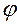 0 n =
0 n = 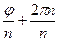 =
= 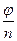 +2
+2 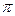 =
= 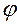 01
01
При k = n +1 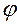 0 ( n+1) =
0 ( n+1) = 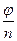 +2
+2 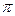 +
+ 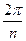 =
= 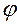 02 и т. д.
02 и т. д.
Таким образом,
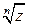 =
= 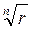 (cos
(cos 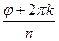 + i⋅sin
+ i⋅sin 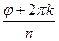 ),
),  k =
k = 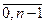 (5)
(5)
Корень n -й степени из комплексного числа z имеет n значений z 0, z 1, z 2,…, zn-1 которые на комплексной плоскости располагаются на окружности радиуса R = 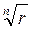 и делят окружность на n равных частей.
и делят окружность на n равных частей.
Date: 2015-07-02; view: 768; Нарушение авторских прав