
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Поле комплексных чисел
|
|
Во множестве рациональных чисел неразрешимо уравнение x 2+1=0, поэтому возникает необходимость расширить множество рациональных чисел так, чтобы в новом множестве данное уравнение было бы разрешимо.
Пусть ℂ=ℝ×ℝ={(a,b)| a,b ∈ℝ}
Определение 1. Элементы (a,b) и (c,d) ∈ℂ называются равными, если а = с и b = d.
Определение 2. Суммой элементов (a,b) и (c,d) ∈ℂ, называется упорядоченная пара 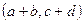 т. е.
т. е. 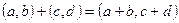 (1).
(1).
Произведением элементов (a,b) и (c,d) ∈ℂ, называется упорядоченная пара 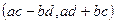 , т. е.
, т. е. 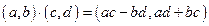 (2).
(2).
Теорема 1. Множество ℂ с заданными на нем операциями «+» и «⋅» по правилам 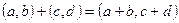 и
и 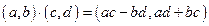 , является полем.
, является полем.
Доказательство.
Из определений следует что заданные на ℂ операции «+» и «⋅» являются алгебраическими, так как ∀(a,b) и (c,d) ∈ℂ, 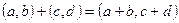 ∈ℂ,
∈ℂ, 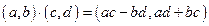 ∈ℂ.
∈ℂ.
I. Покажем что <ℂ,+> абелева группа.
1), 4) Т.к. сложение элементов из ℂ сводится сложению действительных чисел, а на множестве действительных чисел операция “+” ассоциативна и коммутативна, то операция “+”ассоциативна и коммутативна на ℂ.
2) ∃Ө=(0,0) ∈ℂ такое что ∀(a, b)∈ℂ выполняется: (a, b)+Ө=(a +0, b +0)=(a, b)
3 ) ∀ (a,b) ∈ℂ ∃ (-a,-b) ∈ℂ, такое что (a,b)+ (-a,-b) =(a-a, b-b)= (0,0)= Ө
Из пунктов 1)-4) следует что <ℂ,+> абелева группа.
II. Проверим, что в ℂ выполняются дистрибутивные законы
5) ∀ (a1,b1), (a2,b2), (a3,b3) ∈ℂ
[(a1,b1)+(a2,b2)] (a3,b3)=(a1+a2,b1+b2 )⋅(a3,b3)=
((a1+a2) a3-(b1+b2)b3, (a1+a2)b3+ (b1+b2)a3) (3)
(a1,b1)⋅(a3,b3)+(a2,b2)⋅(a3,b3)=(a1a3-b1b3, a1b3+b1a3)+(a2a3-b2b3, a2b3+b2a3)= (a1a3+a2 a3-b1b3-b2b3, a1b3+b1a3+a2b3+b2a3) (4)
Элементы (3) и (4) равны, значит, правый дистрибутивный закон выполняется. Справедливость левого дистрибутивного закона на ℂ следует из коммутативности операции «⋅», см далее аксиому 6).
III. Покажем, что <ℂ#,⋅> - абелева группа.
6) Покажем что операция «⋅» коммутативна на ℂ. ∀ (a1,b1), (a2,b2) ∈ℂ
(a1,b1)⋅(a2,b2)=(a1a2-b1b2,a1b2+a2b1) (5)
(a2,b2)⋅(a1,b1) =(a2a1-b2b1, a2b1+a1b2) (6)
(5)=(6), поскольку умножение действительных чисел коммутативно. Следовательно операция «⋅» коммутативна на ℂ.
7) Покажем, что «⋅» ассоциативна на ℂ# , ∀ (a1,b1), (a2,b2), (a3,b3) ∈ℂ #
[(a1,b1)⋅(a2,b2)]⋅(a3,b3) = (a1a2-b1b2,a1b2+a2b1)⋅(a3,b3)=((a1a2-b1b2)a3 - (a1b2+a2b1)b3, (a1a2-b1b2)b3+(a1b2+a2b1)a3) (7)
(a1,b1)⋅[(a2,b2)⋅(a3,b3)]=(a1,b1)(a2 a3 - b2 b3 , a2 b3+b2 a3)=
(a1(a2 a3 - b2 b3) – b1(a2 b3+b2 a3), a1(a2 b3+b2 a3)+b1(a2 a3 - b2 b3 )) (8)
(7)=(8) в силу дистрибутивных и коммутативных законов на множестве действительных чисел. Следовательно «⋅» ассоциативна на ℂ#.
8) Существование нейтрального элемента относительно операции «⋅», т.е.∃ e =(1,0) ∈ℂ#, такой что ∀(a, b) 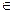 ℂ# выполняется: (a, b)(1,0)=(a⋅ 1- b⋅ 0, a⋅ 0+ b⋅ 1)=(a, b)
ℂ# выполняется: (a, b)(1,0)=(a⋅ 1- b⋅ 0, a⋅ 0+ b⋅ 1)=(a, b)
9) Существование обратного элемента относительно операции «⋅» на ℂ#, т.е. ∀(a, b) 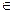 ℂ# ∃(c, d) ∈ℂ#, найдем неизвестные с и d.
ℂ# ∃(c, d) ∈ℂ#, найдем неизвестные с и d.
(a, b)(c, d)=(1,0)
(ac - bd, ad + bc)=(1,0) 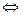 (по определению равенства элементов)
(по определению равенства элементов) 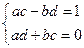 ,
, 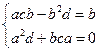 . Вычитая уравнения почленно, получим - b2d-a2d=b;-d(a2+b2)=b;
. Вычитая уравнения почленно, получим - b2d-a2d=b;-d(a2+b2)=b;
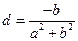 ∈ℝ. Аналогично, исключая неизвестную d, получим
∈ℝ. Аналогично, исключая неизвестную d, получим 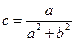 ∈ℝ. Таким образом ∀(a, b) ∈ℂ# существует обратный элемент (
∈ℝ. Таким образом ∀(a, b) ∈ℂ# существует обратный элемент (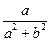 ,
, 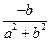 )∈ℂ#
)∈ℂ#
Из пунктов 6)-9) следует что <ℂ#,⋅> - абелева группа.
Из пунктов I-III следует, что ℂ- поле.
Определение 3. Множество ℂ с заданными на нем операциями «+» и «⋅» по правилам 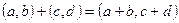 (1)
(1)
и 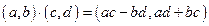 (2)
(2)
называется полем комплексных чисел, а его элементы называются комплексными числами.
Теорема 2. Множество рациональных чисел является подмножеством множества комплексных чисел.
Доказательство. Докажем, что множество рациональных чисел ℝ изоморфно некоторому подмножеству поля ℂ, а именно, подмножеству вида ℝ1={(a,0)׀ a 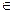 ℝ}Íℂ.
ℝ}Íℂ.
Зададим отображение  :ℝ
:ℝ 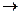 ℝ1, по правилу ∀ a
ℝ1, по правилу ∀ a 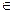 ℝ
ℝ  (a)=(a,0) (*)
(a)=(a,0) (*)
и покажем, что  - изоморфизм колец (полей).
- изоморфизм колец (полей).
1. Покажем что  - гомоморфизм ℝ в ℝ1. Пусть a, b ∈ℝ. Тогда
- гомоморфизм ℝ в ℝ1. Пусть a, b ∈ℝ. Тогда
а)  (a+b)
(a+b) 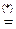 (a + b,0);
(a + b,0);
 (a)+
(a)+  (b)
(b) 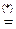 (a,0)+(b,0)
(a,0)+(b,0)  (a+b,0). Значит,
(a+b,0). Значит,  (a+b)=
(a+b)=  (a)+
(a)+  (b).
(b).
б)  (ab)
(ab) 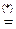 (ab,0).
(ab,0).
 (a)⋅
(a)⋅  (b)
(b) 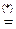 (a,0)(b,0)
(a,0)(b,0) 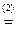 (ab-0,0+0)=(ab,0). Значит,
(ab-0,0+0)=(ab,0). Значит,  (ab)=
(ab)=  (a)⋅
(a)⋅  (b)
(b)
Из а), б) следует, что  - гомоморфизм
- гомоморфизм
2. Покажем, что  - биекция
- биекция
a) Покажем, что  - инъекция. Пусть образы элементов a и b равны, т.е.
- инъекция. Пусть образы элементов a и b равны, т.е.
 (a)=
(a)=  (b)
(b) 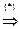 (a,0)=(b,0)
(a,0)=(b,0) 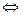 (по определению равенства) a = b.
(по определению равенства) a = b.
б) Покажем, что  - сюръекция. ∀ (a,0)∈ℝ1 ∃ a ∈ℝ, такой что
- сюръекция. ∀ (a,0)∈ℝ1 ∃ a ∈ℝ, такой что  (a)=(a,0).
(a)=(a,0).
Из 1,2 следует, что  - изоморфизм
- изоморфизм 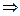 ℝ
ℝ 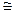 ℝ1. Учитывая, что ℝ1Íℂ, можно считать, что ℝ изоморфно вкладывается в ℂ, отожествляя число a ∈ℝ с парой (a,0)∈ℝ1, т.е. (a,0)
ℝ1. Учитывая, что ℝ1Íℂ, можно считать, что ℝ изоморфно вкладывается в ℂ, отожествляя число a ∈ℝ с парой (a,0)∈ℝ1, т.е. (a,0) 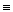 a, и можем считать что ℝÍℂ.
a, и можем считать что ℝÍℂ.
Теорема 3. В поле ℂ уравнение x2+1=0 разрешимо.
Доказательство. Рассмотрим x 2+1=0 как уравнение с коэффициентами из ℂ. А именно, согласно теореме 2, отождествим 1 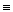 (1,0), 0
(1,0), 0 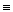 (0,0). Уравнение примет вид x 2+(1,0)=(0,0). Обозначим i =(0,1) и покажем, что i удовлетворяет уравнению. Действительно, i 2=(0,1)(0,1)
(0,0). Уравнение примет вид x 2+(1,0)=(0,0). Обозначим i =(0,1) и покажем, что i удовлетворяет уравнению. Действительно, i 2=(0,1)(0,1) 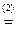 (0-1,0+0)=(-1,0), и i 2+(1,0)=(-1,0)+(1,0)
(0-1,0+0)=(-1,0), и i 2+(1,0)=(-1,0)+(1,0)  (0,0). Cледовательно i – решение уравнения x 2+1=0.
(0,0). Cледовательно i – решение уравнения x 2+1=0.
Отметим что i= (0,1) не принадлежит множеству ℝ1={(a,0)׀ a 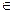 ℝ}
ℝ} 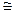 ℝ. Таким образом, i не является действительным числом. Элемент i называют мнимой единицей.
ℝ. Таким образом, i не является действительным числом. Элемент i называют мнимой единицей.
Определение 4. Мнимой единицей называетсякорень i уравнения x 2+1=0, т.е. число, удовлетворяющее условию i 2=-1.
Date: 2015-07-02; view: 1191; Нарушение авторских прав