
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрические величины в школьном курсе математики
|
|
Величина и ее измерение
Говоря далее о величинах, будем иметь в виду скалярную, аддитивную, непрерывную положительную величину. Интуитивно мы представляем себе, что величина может быть больше или меньше, две однородные величины могут складываться, величину можно делить на любое натуральное число, ее можно измерить, причем под измерением обычно понимают сравнение данной величины с другой того же рода, принятой за единицу измерения.. Рассмотрим бесконечное множество В с введенным в нем отношением < (меньше) и операцией + (сложение), т. е. (В,<,+), которое назовем системой однородных величин (или системой величин, или родом величин). Элементы а,b, с,... или а1, а2,... множества В назовем однородными величинами или величинами одного рода.
Система величин (В,<,+) характеризуется следующими свойствами, которые могут быть приняты за исходные предложения (аксиомы) теории величин:
1)  а, b (а>Ь или а=b или b<а) (причем имеет место только одно из трех соотношений).
а, b (а>Ь или а=b или b<а) (причем имеет место только одно из трех соотношений).
2)  а, b, с (а<b и b<с =>а<с) (транзитивность отношения «меньше», а также «больше», которое может быть определено через «меньше», а>b
а, b, с (а<b и b<с =>а<с) (транзитивность отношения «меньше», а также «больше», которое может быть определено через «меньше», а>b  b<а).
b<а).
3)  а, b
а, b 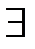 ! с (а+b=с) (замкнутость В относительно сложения).
! с (а+b=с) (замкнутость В относительно сложения).
4)  а, b (а+b=b+а) (коммутативность сложения).
а, b (а+b=b+а) (коммутативность сложения).
5)  а, b, с (а+(b+с)=(а+b)+с) (ассоциативность сложения).
а, b, с (а+(b+с)=(а+b)+с) (ассоциативность сложения).
6)  а, b (а+b>а) (монотонность сложения).
а, b (а+b>а) (монотонность сложения).
7)  а, b а>b =>
а, b а>b => 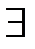 !с (b+с=а)) (возможность вычитания а-b=с),
!с (b+с=а)) (возможность вычитания а-b=с),
8)  а,
а,  n
n  N
N 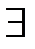 b (nb=а) (возможность деления величины на натуральное число: а:n=b).
b (nb=а) (возможность деления величины на натуральное число: а:n=b).
9)  а, b
а, b 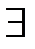 n
n  N (а<nb) (аксиома Архимеда).
N (а<nb) (аксиома Архимеда).
10) пусть даны две последовательности величин из В: а1<а2<...<...; ...<...<b2<b1 причем для любой величины с при достаточно большом номере п bn-аn<с, т. е. члены последовательностей (ап) и (bп) неограниченно приближаются друг к другу. В таком случае существует единственная величина хеВ, которая больше всех аn и меньше всех bn т. е.
 с
с 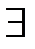 nеN (bn -аn <с)=>
nеN (bn -аn <с)=> 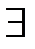 ! х
! х  В
В  n
n  N (аn <х<bn) (аксиома непрерывности).
N (аn <х<bn) (аксиома непрерывности).
Свойства 1-10 полностью определяют понятие системы положительных скалярных величин.
Если какую-нибудь величину е  В принять за единицу измерения» то всякая величина системы В однозначно представлена в виде а=
В принять за единицу измерения» то всякая величина системы В однозначно представлена в виде а= 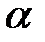 е, где
е, где 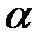 - положительное действительное число (
- положительное действительное число (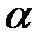
 R+) - мера величины а при единице измерения е. Меру
R+) - мера величины а при единице измерения е. Меру 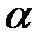 при единице измерения е обозначим через m(а), т. е. если а =
при единице измерения е обозначим через m(а), т. е. если а = 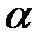 е, то
е, то 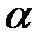 = m(а).
= m(а).
Мера обладает следующими свойствами:
а) m - функция в области определения В и области значения R+, т.е. т отображает В на R+;
б) а<b=>m(a)<m(b) (монотонность меры);
в) m(а+b)=m(а)+m(b) (аддитивность меры);
г) m(е)=1 (мера единицы измерения равна 1).
Перечисленные свойства полностью характеризуют меру т. Существует единственная функция
В 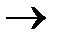 R+, обладающая этими свойствами, а именно мера m(а) величины
R+, обладающая этими свойствами, а именно мера m(а) величины 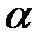 при единице измерения е. Если заменить е на е ', то получится новая мера m'(а)=
при единице измерения е. Если заменить е на е ', то получится новая мера m'(а)= 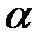 ', причем, т.к. m'(а)=
', причем, т.к. m'(а)= 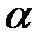 , связь между двумя мерами выразится так: m'(а)=
, связь между двумя мерами выразится так: m'(а)= 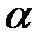 -1m(а).Перечисленные свойства общего понятия величины и меры величины находят применение (в явном или неявном виде) при изучении конкретных геометрических величин (длины, площади и объема) в школе.
-1m(а).Перечисленные свойства общего понятия величины и меры величины находят применение (в явном или неявном виде) при изучении конкретных геометрических величин (длины, площади и объема) в школе.
Методические особенности изучения геометрических величин.
Измерение геометрических величин изучается в школьном курсе дважды, на двух различных уровнях.
На первом, чисто экспериментальном, уровне в начальных классах учатся измерять длины отрезков, площади простейших плоских фигур и объемы простейших пространственных тел. На этом уровне не дается определений длины, площади и объема. Цель состоит в том, чтобы создать у учащихся ясные интуитивные понятия. Рассмотрим некоторые вопросы методики изучения геометрических величин на втором уровне.
Можно ли строго эту теорию построить в школьном курсе? Разные точки зрения, много трудностей, много логических пробелов. Например, в учебнике АЛ. Киселева площадью называется «величина части плоскости, заключенной внутри многоугольника или какой-нибудь другой плоской замкнутой фигуры», далее мы читаем: «Площадь прямоугольника равна произведению его основания на высоту». Далее, правда, есть разъяснение, что это краткая формулировка и надо понимать «число, выражающее площадь прямоугольника в квадратных единицах и т. д.». В сознании учащихся остается только первая формулировка. Аналогично у А.П. Киселева обстоит дело и с определением понятия объема. Объем определяется как величина части пространства, занимаемой геометрическим телом, а дальше - теорема V=аЬс (V - объем прямоугольного параллелепипеда).
Наряду с этим обращает на себя внимание тот разнобой, который имеет место при отыскании числа, выражающего объемы различных тел. Именно поэтому «школьная теория» измерения геометрических величин должна строиться таким образом, чтобы четко вырисовывалась общая схема. Это относится к определениям понятий «длина», «площадь», «объем». Раскрытие связей по общей схеме способствует более глубокому пониманию и прочности знаний. Каждое из трех понятий определяется как вещественное число, удовлетворяющее условиям (а - г), которые характеризуют общее понятие меры множества.
Можно наметить следующую схему теории измерения длин отрезков:
1) определение длины отрезка как вещественного числа, удовлетворяющего условиям;
2) описание процедуры измерения отрезков;
3) установление существования и единственности длины отрезка при данном выборе единицы измерения с использованием аксиомы Архимеда;
4) установление существования отрезка, длина которого при данном выборе единицы измерения равна любому, наперед заданному положительному числу с использованием аксиомы Кантора» геометрического эквивалента аксиомы непрерывности (11).
Разъяснение учащимся старших классов сущности аксиомы Кантора (обычно не рассматривается в школьном курсе) не представляет особых трудностей. Это можно сделать именно в связи с установлением свойства 4.
Случай, когда наперед заданное число - рациональное, не требует применения аксиомы Кантора и выполняется с помощью элементарного построения. Но вот когда число иррациональное (например, х=2,31311311131111...), то при разъяснении приходим к аксиоме Кантора; «Если на прямой дана бесконечная последовательность отрезков А1В2, А2,В2,..., АnВn,... такая, что, во-первых, каждый отрезок лежит внутри предыдущего; во-вторых, нет отрезка, лежащего внутри всех отрезков этой последовательности, то существует точка, лежащая внутри всех отрезков этой последовательности». Единственность этой точки непосредственно следует из аксиомы. И таким образом, строим отрезок х.
Теория измерения площадей и объемов в некоторой части аналогичны. Подчеркивание этой аналогии в процессе обучения -эффективное средство формирования понятия о методике построения этих теорий.
Аналогия заключается в выборе единицы измерения (квадрат со стороной 1 - куб с ребром 1), а также в последовательности и е доказательств предложении. Однако это не распространяется на всю теорию. Например, нельзя проводить аналогию в вопросах о равновеликости и равносоставленности площадей и объемов, хотя определения этих понятий вводятся аналогично. Но, если всякие равновеликие многоугольники равносоставлены, то этого нельзя сказать о равновеликих многоугольниках:«Два многоугольника (многогранника), которые можно разложить на одинаковое число попарно конгруэнтных многоугольников (многогранников), называются равносоставленными ».
Вопрос
Методика изучения темы «Векторы»
В математике обычно имеют дело с так называемым свободным вектором (вектором, не связанным ни с какой прямой и ни с какой фиксированной точкой). Следует отметить, что в математике вектор рассматривается как элемент векторного пространства, но в школьном курсе математики понятие «векторное пространство» не изучается. Поэтому и выделяют различные подходы к введению вектора. Каждый из этих подходов имеет свои достоинства и недостатки. И фактически ни один из них не является идеальным и логически безупречным. Так, в пособии под редакцией Колмогорова А. Н. дается такое определение: «В геометрии параллельные переносы имеют и другое название - их называют векторами». Данное определение основано на рассуждениях, что вектор - это объект, характеризуемый направлением и длиной. Однако, как известно, теми же самыми признаками характеризуется и параллельный перенос. Поэтому представляется наиболее естественным всякий параллельный перенос называть вектором.
Новое определение вектора не связано с понятием направленного отрезка. Под вектором понимают либо множество упорядоченных пар точек, задающих некоторый параллельный перенос, либо сам этот перенос. Рассмотрим множество всех пар точек плоскости. Для элементов рассматриваемого множества введем следующее отношение: пары (А, В) и (С, D), если [АВ)  [СВ) и, |АВ|=|СО|. Это те пары точек, которые задают один и тот же параллельный перенос. Эквивалентными между собой будем считать и пары, у которых первая точка совпадает со второй. Легко проверить, что такое отношение эквивалентности обладает свойствами рефлексивности, симметричности и транзитивности. Данное отношение эквивалентности разбивает множество пар точек плоскости на непересекающиеся подмножества (классы), элементами которых являются эквивалентные пары. Каждое из таких подмножеств можно назвать вектором. Заметим, что при данной трактовке вектора направленный отрезок АВ выступает как удобное наглядное изображение вектора. Однако в статье А. Д. Александрова «Понятие вектора в физике и геометрии» говорится о том, что неправильно определять вектор как направленный отрезок. В этой же статье в качестве наиболее удачного предлагается такое определение вектора; «Вектором в геометрии называется направленный отрезок, рассматриваемый с точностью до выбора его начала, т.е. равные друг другу направленные отрезки считаются представителями или изображениями одного и того же вектора. Данный вектор -это любой из таких отрезков». «Направленный отрезок называется вектором» - так определяется данное понятие в учебниках. Отличительной чертой изложения векторов здесь является широкое использование координатного метода. При этом широко применяются свойства параллельного переноса, который сам вводится с использованием координат. С помощью параллельного переноса вводятся такие понятия, как «одинаково направленные векторы», «равенство векторов». У этого подхода к введению векторов есть достоинства и недостатки. К достоинствам можно отнести отсутствие трудностей, связанных с введением операций над векторами и законов векторной алгебры. К недостаткам следует отнести то, что геометрический смысл этих операций отодвигается на второй план, а приложения векторов в физике и в геометрии практически не рассматриваются. Эти недостатки частично устранены в учебнике Л.С. Атанасяна и др. «Геометрия 7-9 кл.», где сначала изложена декартова система координат, затем тема «Векторы» (вектор и операции над векторами рассматриваются с геометрической точки зрения, уделяется внимание их приложениям) и только потом идет векторная алгебра.
[СВ) и, |АВ|=|СО|. Это те пары точек, которые задают один и тот же параллельный перенос. Эквивалентными между собой будем считать и пары, у которых первая точка совпадает со второй. Легко проверить, что такое отношение эквивалентности обладает свойствами рефлексивности, симметричности и транзитивности. Данное отношение эквивалентности разбивает множество пар точек плоскости на непересекающиеся подмножества (классы), элементами которых являются эквивалентные пары. Каждое из таких подмножеств можно назвать вектором. Заметим, что при данной трактовке вектора направленный отрезок АВ выступает как удобное наглядное изображение вектора. Однако в статье А. Д. Александрова «Понятие вектора в физике и геометрии» говорится о том, что неправильно определять вектор как направленный отрезок. В этой же статье в качестве наиболее удачного предлагается такое определение вектора; «Вектором в геометрии называется направленный отрезок, рассматриваемый с точностью до выбора его начала, т.е. равные друг другу направленные отрезки считаются представителями или изображениями одного и того же вектора. Данный вектор -это любой из таких отрезков». «Направленный отрезок называется вектором» - так определяется данное понятие в учебниках. Отличительной чертой изложения векторов здесь является широкое использование координатного метода. При этом широко применяются свойства параллельного переноса, который сам вводится с использованием координат. С помощью параллельного переноса вводятся такие понятия, как «одинаково направленные векторы», «равенство векторов». У этого подхода к введению векторов есть достоинства и недостатки. К достоинствам можно отнести отсутствие трудностей, связанных с введением операций над векторами и законов векторной алгебры. К недостаткам следует отнести то, что геометрический смысл этих операций отодвигается на второй план, а приложения векторов в физике и в геометрии практически не рассматриваются. Эти недостатки частично устранены в учебнике Л.С. Атанасяна и др. «Геометрия 7-9 кл.», где сначала изложена декартова система координат, затем тема «Векторы» (вектор и операции над векторами рассматриваются с геометрической точки зрения, уделяется внимание их приложениям) и только потом идет векторная алгебра.
Содержание темы в школьном курсе математики и некоторые особенности ее изучения
Операции над векторами.
Операции над векторами, которые изучаются в средней школе, следующие;
- сложение векторов (вычитание);
- скалярное произведение векторов;
Чаще всего эти операции вводятся в геометрической форме (Л.С. Атанасян).
Отличительной чертой учебного пособия по геометрии А.В. По-горелова является то, что все операции над векторами вводятся в координатной форме. (Фактический материал см. по соответствующим учебникам).
Важным для приложений векторов является тот факт, что любой вектор а(аиа2) допускает разложение в виде 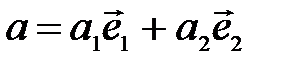 , где е
, где е 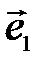 ,
, 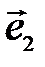 -единичные векторы, имеющие направления положительных координатных полуосей, их называют координатными векторами, или ортами.
-единичные векторы, имеющие направления положительных координатных полуосей, их называют координатными векторами, или ортами.
В этой теме обязательно доказательство теоремы о скалярном произведении векторов (доказательство знать), поскольку ряд важных следствий из этой теоремы, а также свойства скалярного произведения позволяют применять векторы к доказательству теорем и решению задач.
Применение векторов при доказательстве теорем.
С помощью векторов могут быть доказаны следующие теоремы:
- средняя линия треугольника параллельна его третьей стороне и равна ее половине;
- сумма квадратов длин диагоналей параллелограмма равна гумме квадратов длин всех его сторон;
- диагонали ромба взаимно перпендикулярны;
- диагонали в прямоугольнике имеют равные длины; и т.д. (одну доказать).
Методика решения геометрических задач с помощью векторов.
Введенный в среднюю школу векторный аппарат дает новый метод для решения геометрических задач. По значимости его мож-ю сравнить с методом составления уравнений. Так как этот метод является новым для учащихся, необходимо:
а) заинтересовать учащихся, показав им эффективность его использования на специально подобранных задачах;
в) обучать учащихся некоторым эвристикам (системе опредеделённых правил, помогающих найти ключ к решению задачи), которые помогут создать у них навык в его применении;
с) обучать учащихся этому методу достаточно на простых задачах, не отвлекая внимание на трудности чисто геометрического содержания.
Вопрос
Date: 2015-06-11; view: 2040; Нарушение авторских прав