Вопрос - 9 вопрос

II. Иррациональные уравнения

Иррациональным называется уравнение, в котором переменная содержится под знаком корня. Решаются такие уравнения возведением обеих частей в степень. При возведении в четную степень возможно расширение области определения заданного уравнения. Поэтому при решении таких иррациональных уравнений обязательны проверка или нахождение области допустимых значений уравнений. При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется. Иррациональные уравнения стандартного вида можно решить пользуясь следующим правилом:

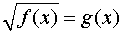
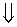
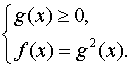
Решение иррациональных уравнений стандартного вида:

Учебный материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики, а его изучение в современной методике обучения математике организовано в отдельную содержательно-методическую линию. Отметим, что с уравнениями учащиеся встречаются еще в начальной школе. Вспомним, например, такую запись: 2+ =5, которая представляет собой уравнение, только неизвестное здесь обозначено не привычно нам буквой, а пустым прямоугольником, в который необходимо вписать соответствующее число. Также не представляет труда привести и примеры уравнений, встречаемых в основной и старшей школе. Сказанное еще раз подчеркивает важность данной темы для разработки методики ее изучения в различных классах средней школы. Здесь мы придерживаемся той позиции, что при расширении класса изучаемых уравнений основные способы и методы их решения остаются прежними, обогащаясь при этом лишь специальными, свойственными для того или иного нового класса уравнений, а поэтому соответствующая методика обучения должна быть направлена на формирование общего приема решения уравнения или неравенства вкупе с изучением специальных приемов. Этапы общего приема решения уравнения, неравенства мы уже приводили (см. статью «Обучение учащихся решению иррациональных неравенств»), поэтому здесь кратко напомним их: 1. Определить вид уравнения, неравенства. 2. Определить стандартное оно или нет. 3. Если стандартное, то решить в соответствии с известным правилом, алгоритмом. 4. Если нестандартное, то выяснить, какие преобразования необходимо выполнить, чтобы свести его к стандартному, либо перейти к использованию искусственных приемов решения. 5. Выполнить эти преобразования. 6. Сделать проверку. 7. Записать ответ. Вполне естественно, что для каждого класса уравнений или неравенств общий прием может претерпевать некоторые уточнения, которые окажут влияние на методику их изучения. Так, относительно иррациональных уравнений, на наш взгляд, важнее показать учащимся основные приемы их решения, чем делать акцент на определении вида уравнения – стандартное оно или нет. Для сравнения: при решении, например, тригонометрического уравнения важно знать его вид, ибо вид тригонометрического уравнения во многом определяет и прием его решения. Напомним, что существует два основных метода решения уравнений и неравенств с переменной – алгебраический и графический. Основная идея алгебраического метода решения иррациональных уравнений – это сведение данного уравнения с помощью различных преобразований к рациональному уравнению, последнее же решается с помощью уже известных приемов решения. При этом выделяют два основных способа избавления от иррациональности: 1) возведение в степень, 2) введение новой переменной.

Рассмотрим два примера, характеризующих данные способы.

Пример 1. + . = .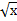

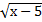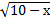Решение данного уравнения довольно просто: сведение его к рациональному основано на возведении обеих частей в квадрат:

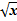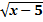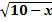( + )²= ( )²

х+2 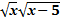+(х-5)=10-х

2 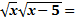3(х-5)

(2 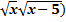²=(3(х-5))²

4х(х-5)-9(х-5)²=0

(х-5)(4х-9х+45)=0

х₁=5, х₂=9.

Проверка подстановкой показывает, что x₁=5 – корень уравнения, x₂=9 – посторонний корень.

При решении иррационального уравнения чаще всего стараются преобразовать его к рациональному уравнению либо возведением обеих его частей в степень, либо введением новой переменной. Второй аспект, который мы хотели бы рассмотреть в данной статье, связан с выполнением проверки. Известно, что если все уравнения (неравенства), полученные из данного последовательным их преобразованием, равносильны, то проверка найденных значений переменной не является логически необходимой, она проводится только в порядке контроля вычислений или по методическим соображениям (например, формирование понятия корня уравнения, формирование умения выполнять арифметические операции и т.п.). Подчеркнем, что в логике развития содержательно-методической линии уравнений и неравенств иррациональные уравнения – первый класс уравнений, методы решения которых предполагают логически необходимое выполнение проверки найденных корней (прежде изучались рациональные уравнения, их преобразования равносильны на области их допустимых значений). Поэтому в данной теме следует вести разговор (если это не было сделано раньше) о равносильных и неравносильных преобразованиях. Для уравнений выполнение проверки можно осуществить двумя способами: а) непосредственная подстановка найденных значений в исходное уравнение – проверка подстановкой (данным способом мы воспользовались выше при решении двух примеров); б) установление равносильности выполняемых преобразований. Чтобы показать суть второго способа, обратимся к решенному нами ранее уравнению (пример 1). Так, при его решении мы лишь два раза нарушали равносильность преобразований – в обоих случаях при возведении в квадрат. Однако на множестве {5} левая и правая части возводимых в квадрат уравнений неотрицательны, следовательно, на этом множестве все преобразования были равносильны, поэтому найденное значение x=5 – корень уравнения. Второй найденный корень x=9 является посторонним, поскольку перед вторым возведением в квадрат (третья строчка решения) замечаем, что при x=9 правая часть уравнения отрицательна, а левая – положительна, чего не может быть (здесь возведение в квадрат привело к уравнению-следствию, имеющему, в отличие от исходного, два корня). На практике следует уделять внимание обоим названным способам. В некоторых случаях целесообразно и наиболее просто выполнить проверку подстановкой, иногда же проверка подстановкой может привести к сложным вычислениям – здесь уместно установление равносильности выполняемых преобразований. Более того, при решении неравенств (если ответ представляет собой некоторый промежуток) проверка подстановкой невозможна в принципе. Приведенные рассуждения о проверке найденных корней обуславливают целесообразность выделения двух подходов при алгебраическом методе решения иррациональных неравенств: с использованием равносильных преобразований и без использования равносильных преобразований. Учителю следует на простых примерах показывать учащимся суть каждого подхода, его преимущества и недостатки. Выбор же того или иного подхода определяется каждым конкретным решаемым уравнением. На наш взгляд, прежде чем начинать выполнять преобразования самого уравнения, следует установить систему неравенств, задающих область допустимых значений уравнения, оценить трудоемкость ее решения, а уже потом делать выводы: выполнять ли преобразования уравнения с последующей проверкой корней подстановкой, либо свести решение уравнения к решению равносильной ему системе. Таким образом, алгебраический метод решения иррационального уравнения пред- полагает некоторую свободу выбора подхода к его решению. При этом учителю следует добиваться от учащихся осознанного и обоснованного выбора наиболее рационального подхода, причем следует помнить и о том, что наряду с алгебраическим рассматривают графический и другие методы решения иррациональных уравнений.

Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.

Прежде чем приступить к решению сложных уравнений учащиеся должны научиться решать простейшие иррациональные уравнения. К простейшим иррациональным уравнениям относятся уравнения вида:.

Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.

Главный способ избавиться от корня и получить рациональное уравнение – возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее «освобождение» от радикалов по формуле.

Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному.

При возведении уравнения в четную степень получается уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения, но не возможна потеря корней. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.

Так как могут появиться посторонние корни, то необходимо делать проверку, подставляя найденные значения неизвестной только в первоначальное уравнение, а не в какие-то промежуточные.

Рассмотрим применение данного метода для решения иррациональных уравнений вида

Иррациональные неравенства – довольно сложный раздел школьного курса математики, а если учесть, что на его изучение отведено крайне мало времени, то становится ясно, что учащиеся как правило это раздел не усваивают. Даже у тех учащихся, что успешно решают иррациональные уравнения, часто возникают проблемы при решении иррациональных неравенств. Решение иррациональных неравенств осложняется тем обстоятельством, что здесь, как правило, исключена возможность проверки, поэтому надо стараться делать все преобразования равносильными.

Если в любом иррациональном уравнении заменить знак равенства на один из знаков неравенства: >,, <,, то получим иррациональное неравенство. [19] Поэтому под иррациональным неравенством будем понимать неравенство, в котором неизвестные величины находятся под знаком корня. [16]

Способ решения таких неравенств состоит в преобразовании их к рациональным неравенствам путем возведения обеих частей неравенства в степень.

Чтобы избежать ошибок при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, то есть найти ОДЗ этого неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или ее частях.

При решении иррациональных неравенств следует запомнить правило: при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное данному неравенству. [16]

Но если при решении уравнений в результате возведения четную степень мы могли получить посторонние корни (которые, как правило легко проверить) и не могли потерять корни, то корни неравенства при бездумном возведении в четную степень могут одновременно и теряться, и приобретаться. [8]

Например, возведя в квадрат:

- верное неравенство, мы получим верное неравенство;

- верное неравенство, мы получим неверное неравенство;

- неверное неравенство, мы получим верное неравенство;

- неверное неравенство, мы получим неверное неравенство.

Вы видите, что возможны все комбинации верных и неверных неравенств.

Однако верно основное используемое здесь утверждение: если обе части неравенства возводят в четную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.

Метод сведения к эквивалентной системе или совокупности рациональных неравенств

Основным методом решения иррациональных неравенств является сведение исходного неравенства к равносильной системе или совокупности систем рациональных неравенств.