Методика изучения линейной функции

В соответствии со схемой, изучения линейной ф-ии начинается с рассмотрения задач:

1. На шоссе расположены пункты А и В удаленные друг от друга на 20 км, мотоцикл выехал из В в направлении противоположном А со скоростью 50км/ч. За t часов мотоциклист проедет 50*t и будет находиться от А на расстоянии 50t+20км => зависимость этого расстояния от времени движения можно выразить ф-лой S=50t+20, где t≥0.

2. Ученик купил тетради по 3 коп за штуку и ручку за 35 коп. Какова стоимость всей покупки. Стоимость покупки зависит от числа тетрадей, если х – число тетрадей, а у –стоимость покупки, то у=3х+35. Вывод каждому х соответствует у, т.е. в обоих случаях мы встретились с функциями заданными формулами вида у=кх+в, где х – независимая переменная, к и в – некоторые числа. Такие функции называются линейными.

Опр: линейной функцией называется функция, которую можно задать формулой вида: у=кх+в, где х – независимая переменная, к и в - некоторые числа. Даже рассматривая конкретную функцию учащиеся выясняют, что является графиком линейной функции. Например, у=0,5х-2, составляют таблицу, отмечают точки на координатной плоскости. Без доказательства принимается, что графиком линейной функции является прямая. Необходимо научить учащихся строить график функции по двум точкам, по точкам пересечения функции с координатными осями. х=0, у=b; y=0, x=a. В ходе решения задач на построение графиков функций учащиеся проводят элементарные исследования, устанавливают свойства.

Вопрос

В математике тригонометрические функции часто опре­деляются аналитическим путем: с помощью степенных рядов, как решения дифференциального уравнения, как интегральные представления. Тригонометрические функ­ции могут быть определены геометрическими средствами. Существуют различные варианты изложения элементов тригонометрии в школьном курсе математики. Они основа­ны на применении системы координат, векторов, геомет­рических преобразований.

Традиционная методическая схема изучения тригоно­метрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямо­угольного треугольника; 2) затем введенные понятия обо­бщаются для углов от 0° до 180°; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.

Далее вводятся определения тригон. Ф. Конкретнее рассмотрим введение определения cos а, придерживаясь следующей мето­дической схемы: 1) построить на миллиметровой бумаге прямоугольный треугольник ABC; 2) обозначить величину острого угла А буквой а; 3) измерить (по клеткам) прилежащий катет АС и гипотенузу АВ; 4) вычислить отношение 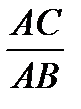; 5) записать значение cos а (делается следующая запись: cos a 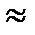..., в которой для а не ука­зывается его конкретное значение); 6) измерить транспор­тиром угол а, найти его величину и записать значение косинуса этого угла данного прямоугольного треугольни­ка; 7) проделать пп. 1—6 для острых углов других прямо­угольных треугольников. Определенные трудности в изучении элементов триго­нометрии порождает следующая теорема: «Косинус угла а зависит только от градусной меры угла». Необходимость изучения данной теоремы можно разъяснить учащимся следующим образом. Пусть требуется на основании определения найти cos 37°. Предположим что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 37°, они построят прямоугольный треугольник (каждый свой) с углом в 37° измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 37°. Есть ли гарантия что каждый ученик получит один и тот же ответ? Этот[ вопрос возникает по той причине, что каждый ученщ строит свой прямоугольный треугольник, получает свое значения длин прилежащего катета и гипотенузы. Так может быть, и искомое отношение у каждого ученика буде какое-то свое? Понятно, что если бы значение cos 37^е при переходе от одного прямоугольного треугольника другому изменялось, то ценность такого понятия в математике была бы невелика. Изучаемая теорема является ответом на поставленные вопросы. Она утверждает, что' косинус острого угла зависит не от выбора прямоугольно­го треугольника, а только от меры угла.

При решении прямоугольных тре­угольников необходимо обратить внимание учащихся на тот факт, что с каждой из формул для cos a, sin а и tg а связываются еще две формулы:

Всего, таким образом, получается девять формул. Назовите (с учетом приведенных выше формул) основные виды задач на решение прямоугольного треугольника.

Разработайте опорный конспект для доказательства следующих тригонометрических тождеств:

sin² a +cos² a = 1, tg² a 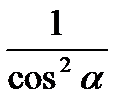+1 = , 1 + =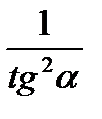

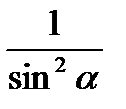
sin (90° — a) = cos a, cos (90° — a) = sin a.

Определения косинуса, синуса и тангенса углов от 0° до 180° являются генетическими. В этих определениях указываются построения и вычисления, позволяющие най­ти значение тригонометрической функции. В пособии [23] говорится следующее: «До сих пор значения синуса, косинуса и тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°. Возьмем окружность на плоскости ху с центром в начале координат и радиусом R. Пусть а — острый угол, который образует радиус ОА с положительной полуосью х. Пусть х и у — координаты точки А. Значения sin a, cos ос и tg а для острого угла а выражаются через координаты точки А. Именно:

cos a = 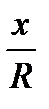Sin a= Tg a=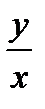

Определим теперь значения sin a, cos a и tg a этими формулами для любого угла а. (Для tg а угол а = 90° исключается.).

В курсе алгебры и начал анализа осуществляется последний, заключительный этап изучения тригонометри­ческих функций. В него входят: 1) закрепление пред­ставлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот; 2) формирование представлений об углах с градусной мерой, большей 360°; формирование представ­лений об углах с положительной и отрицательной градус­ными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа); 3) описание тригонометрических функций на языке ра­дианной меры угла; 4) утверждение функциональной точки зрения на cos a, sin а и tg а (трактовка cos a, sin а и tg а как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т. д.); 5) повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом к которым является тождество cos (а + р) = cos а cos (3 — sin а sin (3 (формула косинуса суммы двух аргументов); 6) применение тригонометриче­ских тождеств в тождественных преобразованиях и при решении задач по стереометрии.

Вопрос

Решение уравнений составляет алгебраическую часть школьного курса. Задачи и методы алгебры возникли в результате поисков общих приемов для решения однотипных арифметических задач, эти приемы заключались в составлении и решении уравнений поэтому алгебра долгое время воспринималась как наука об уравнениях, сюда же привлекали и тождественные преобразования, которые подчинялись цели решения уравнений. В учебно-методической литературе уравнение рассматривается как аналитическая запись задачи об отыскании совокупности тех значений переменных при которых выражения в левой и правой части принимают равные значения. Согласно этому уравнение – это не само равенство, а лишь вопрос о $-и значений неизвестных, при которых имеет место равенство, при этом отождествляются понятия: уравнение, решить уравнение. Тем не менее термин уравнение часто употребляется вне связи с задачей отыскания его решения так например говорят о уравнении касательной, уравнении движения точки и т.п. Учащиеся начинают решать уравнения рано. В 1 кл. решают уравнения на основе правил нахождения неизвестного слагаемого, вычитаемого, уменьшаемого. Во 2 кл. – на основе правил нахождения неизвестного множителя, делимого, делителя. В 3 – 4 кл. умения закрепляются. В 5 кл. – уравнение определяется как равенство, содержащее неизвестные числа. Число при котором уравнение превращается в верное называется корнем уравнения. Решить уравнение – найти все его корни. В 6 кл. – возможность прибавить к обеим частям уравнения одно и то же число. Вводится перенос членов уравнения. В 7 кл. уравнение определяется как равенство содержащее переменную. Формулируется свойство равносильности. Решение линейного уравнения с параметрами. Понятие системы и рассматривается система линейных уравнений. Построение графика уравнения ax+by=c. В 8 кл. – квадратные уравнения. Решаются уравнения ax²+bx +c=0. решение дробно – рац. уравнений. В 9 кл. продолжается изучение уравнений и систем уравнений. Знакомятся с понятием степень целого рац. уравнения, что позволяет решать уравнения 3,4 степени. Система с двумя параметрами, графическое решение уравнений. Разработанный аппарат решения уравнений позволяет решать содержательные текстовые задачи методом уравнений. Программой предусматривается, чтобы в процессе обучения учащихся усвоили математические ЗиУ, усвоили важнейшие понятия курса, терминологию и язык, основ-е термины, формулы, правила, приемы и методы решения задач. Виды уравнений: линейные – ax+by=c, квадратные ax²+bx+c=0, дробно - рациональные, уравнение степени, логарифмические, показательные, тригонометрические. Методы решения: алгебраический (подстановка, замена, умножение на число), графический. Метод. замечания. 1. Понятие уравнений тесно связано с понятием корень уравнения, решить уравнение, система уравнений. Если уч-ся усваивают эти понятия, то => понимание теории и решения задач. Необходимо систематически разъяснять их смысл, приводя примеры. 2. При изучении уравнений уч-ся должны усвоить идею равносильности, использовать свойства равносильности уравнений и тождественных преобразований => рациональное решение уравнений. Целесообразно от уравнений с дробными коэффициентами перейти к уравнениям с целыми коэффициентами. 3. Необходимо обучить уч-ся алгоритмическим приемам. 4. Хорошим применением уравнений является текстовые задачи по алгебре. 5. для линии уравнений характерна направленность на установление связей с остальным содержанием курса математики тесно связано с числовой теорией, с функциональной линией, что служит наглядностью при решении уравнений. Без линии тождественных преобразований невозможно решение любого уравнения и их систем.

Вопрос

Изучение вопроса о квадратичной функции осуществляется в следующей последовательности, сначала изучается у=2x². Задача: найти зависимость площади поверхности куба от длинны его ребра. Пусть длинна ребра куба х см, площадь поверхности куба равна 6х² см², если обозначить х поверхности куба через у, то получаем равенство у=6x². В рассматриваемой задаче мы встретились с ф-ией, которая задается ф-лой у=ах², где х – независимая переменная, а – некоторое число. Итак рассмотрим ф-ию у=ах², выясним что является графиком этой ф-ии, каковы св-ва этой ф-ии:

1) при а=1, у=х² – графиком является парабола.

2) при а=1,5 у=1,5х². Составляют таблицу, строят график и рассматривая график учащиеся приходят к выводу, что график ф-ии у=1,5х² можно получить из параболы у=х², растяжением по оси х а полтора раза.

3) при а=0,5, у=0,5 х² – составляют таблицу, аналогично рассматривая график данной ф-ии

приходят к выводу, что график ф-ии у=0,5х² можно получить из параболы у= х² сжатием по оси х в два раза.

4) При а=-0,5, у=-0,5 х² – график ф-ии у=-0,5 х² может быть получен из графика ф-ии у=0,5 х² с помощью симметрии относительно оси х.

Вывод график ф-ии у=ах² при любом значении а≠0 называется параболой, затем:

1) при любом а, если х=0, то у=0 => график ф-ии проходит через начало координат.

2) при a>0, если х≠0, то у>0; при а<0, если х≠0, то у<0 (расположенные в координатной плоскости)

3) противоположным значениям аргумента соответствует равные значения ф-ии, следовательно график ф-ии симметричен относительно оси ординат

4) при a>0, у уменьшается при xє(-∞;0], увеличивается при xє[0;+∞), при а<0, у увеличивается при xє(-∞;0], уменьшается при xє[0;+∞). Точки пересечения параболы с ее осью симметрии называется вершиной параболы

График ф-ии y=ax²+bx+c

Рассматриваются, записанные на доске ф-ии y=x²-15x+8, y=-0,8x²+7x-15, учитель обращает внимание учащихся на то что правые части являются квадратными трехчленами, ф-ии называются квадратичными.

Опр: квадратичной ф-ией называется ф-ия, которую можно задать ф-лой y=ax²+bx+c, где х – независимая переменная, a,b,c – некоторые числа, причем а ≠ 0.

Для выяснения, что является графиком квадратичной ф-ии рассматривают пример: 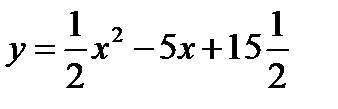. Показывают, что график данной ф-ии может быть получет из графика ф-ии у=½х² с помощью параллельного переноса. Для этого выполняют некоторые преобразования: выделяют квадрат двучлена в правой части: 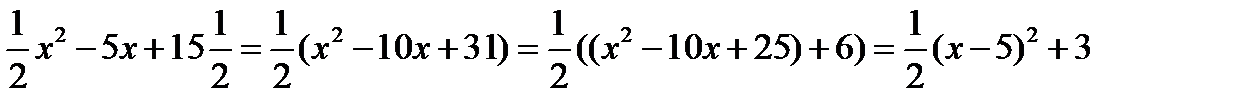, строят в одной сис-ме координат графики ф-ий у=½х² и у=½(х-5)²+3. Рассмотрим графики данных ф-ий. Учащиеся приходят к выводу, что любая точка графика у=½(х-5)²+3 может быть получена параллельным переносом соответствующих точек графика ф-ии 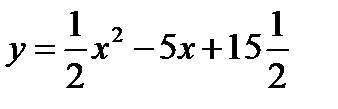, т.е. парал-ным переносом при котором всякая точка с координатами (х₀;y₀) переходят в точку с координатами (х₀+5;y₀+3). Из свойств параллельного переноса следует, что графиком ф-ии у=½(х-5)²+3, а значит и ф-ии 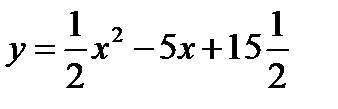является парабола, равная параболе у=½х². Далее рассматривают ф-ию в общем виде y=ax²+bx+c. В результате преобразований получают у=а(х+b/2а)² – (b²-4ас)/4а. Эта формула имеет вид y=a(x-m)²+n, m=(-b)/2a, n=(b²-4ас)/4а, можно докь-ть, что график функции y=a(x-m)²+n получился из графика ф-ии y=ax² с помощью пар. переноса при котором точка а с координатами (х₀;y₀) переходит в точку с координатами (х₀+m;y₀+n) => графиком ф-ии y=ax²+bx+c является парабола, равная y=ax² , ее вершиной является точка с координатами (m;n).

Для практики удобно строить график квадратичной ф-ии по нескольким точкам: 1) точки с координатами (m,n); 2) точки пересечения с осью Ох: y=0, 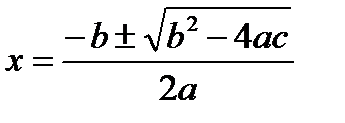; 3) точка пересечения с осью Оу х=0, у=с. Далее рассматривают свойства функции: область определения функции, область значения функции, монотонность, точки пересечения с координатными осями, промежутки знакопостоянства, наибольшее и наименьшее значение ее.