Приведение общего уравнения поверхности второго порядка к каноническому виду

Общее уравнение поверхности второго порядка имеет вид:

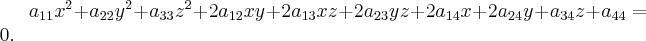
Квадратичная часть этого уравнения - это квадратичная форма

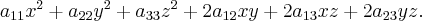
Матрица квадратичной формы:

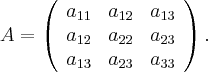
В каноническом уравнении матрица квадратичной части должно быть диагональной. Нам известно, что существует ортогональное преобразование координат такое, что матрица квадратичной формы в новых координатах имеет диагональный вид. Новый базис образуется из собственных векторов матрицы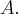

Итак, для того чтоб привести общее уравнение к каноническому виду нужно

· найти ортогональный базис из собственных векторов матрицы;

· перейти к новой системе координат, в которой матрица квадратичной части является диагональной;

· осуществить параллельный перенос начала координат таким образом, чтобы уравнение приняло канонический вид (например, в центр вершину поверхности).

Итак, схема приведения общего уравнения поверхности к каноническому виду такая же как и для кривой. Но есть некоторые отличия, например, когда собственное число матрицы квадратичной формы имеет кратность больше 1. Разберем на примере.

Пример. Привести к каноническому виду уравнение поверхности

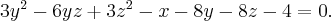
Найти каноническую систему координат.

Выписываем матрицу квадратичной части:

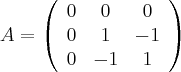
Характеристический многочлен этой матрицы:

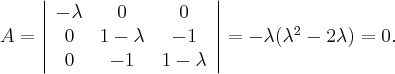
Его корни, собственные числа матрицы :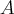

Ищем собственные векторы.

Для 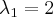собственный вектор находится из системы уравнений Матрица этой системы: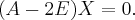

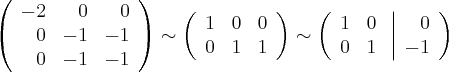
Итак, собственный вектор имеет направление Нормируем его (делим на длину) и берем в качестве первого нового базисного вектора

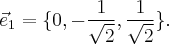
Для 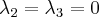собственные векторы находятся из системы уравнений Матрица этой системы: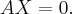

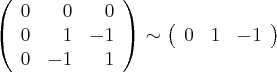
Итак, собственные векторы, соответствующие собственному числу 0, образуют двумерный подпространство, ортогональный вектору 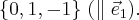Выберем какой-нибудь вектор из этого подпространства, например 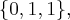нормируем его (делим на длину) и берем в качестве второго нового базисного вектора 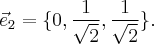Третий базисный вектор можно найти как 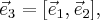он будет принадлежать подпространства собственных векторов для 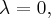кроме того 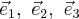образуют ортонормированный положительно ориентированный базис. Итак,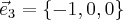

Переходим к новой системе координат. Напомним, что старые координаты 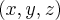связаны с новыми 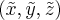следующим образом:

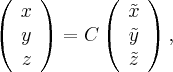
где - матрица перехода к новому базису, ее столбиками есть координаты новых базисных векторов в старом базисе.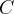

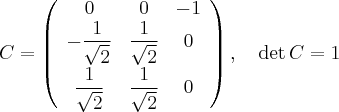
Преобразование координат

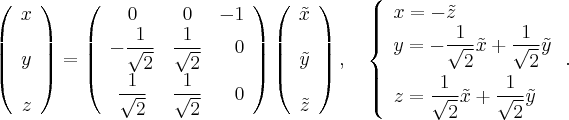
Подставляем эти выражения в уравнение поверхности. В квадратичную часть подставлять не нужно, по известной теореме в базисе из собственных векторов матрица квадратичной части имеет диагональный вид, где диагонали стоят собственные числа. Нужно подставить эти выражения только в линейную часть:

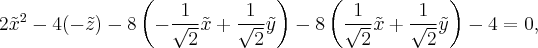
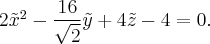
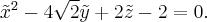
Это уравнение параболического цилиндра, но еще не каноническое. Нам нужно сделать еще оборот вокруг оси 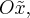так как в плоскости 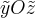мы выбирали базисные векторы 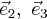произвольным образом, а они оказались не каноническими. Вращение вокруг оси 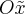задается матрицей:

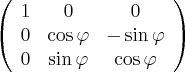
Итак, нам нужно найти угол 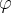, на который мы должны сделать оборот. В общем случае это делается следующим образом. Мы имеем

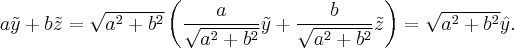
Итак, 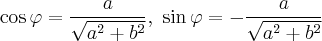В нашем случае

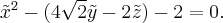
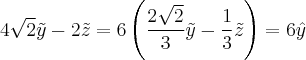
Итак,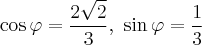

После последующего преобразования координат

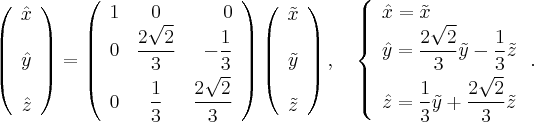
имеем

Делаем параллельный перенос

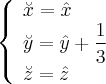
и получаем в новой системе координат каноническое уравнение параболического цилиндра:

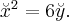
Теперь нужно выписать общее преобразование координат, то есть выразить координаты 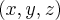через 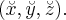Напомним, что обратная ортогональной матрица совпадает с транспонированной. Имеем

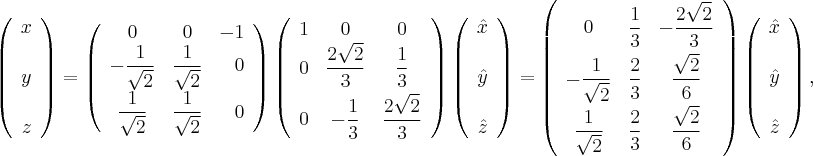
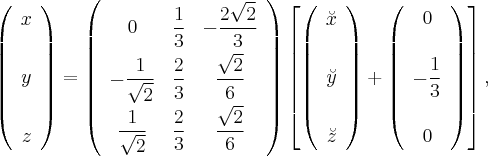
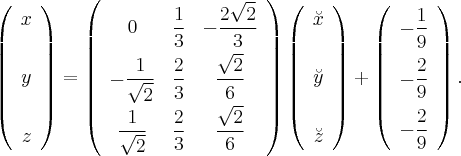
Итак, это превращение дает нам каноническую систему координат: ее начало находится в точке 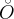с координатами 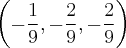, базисные векторы новых координатных осей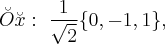

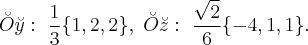
Date: 2015-07-01; view: 13815; Нарушение авторских прав