
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Самосопряжённых оператор в евклидовом пространстве
|
|
Пусть линейный оператор, которому в ортонормированном базисе отвечает матрица 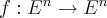
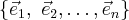
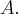
Оператор 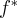 называется сопряженным к оператору
называется сопряженным к оператору  если для любых векторов
если для любых векторов 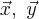 выполняется
выполняется
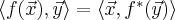
Выясним какая матрица соответствует сопряженное оператору. Если  - матрица оператора
- матрица оператора  а матрица - матрица сопряженного оператора то имеем
а матрица - матрица сопряженного оператора то имеем 
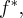
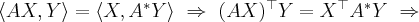
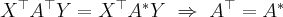
Итак сопряженных оператору соответствует транспонированная матрица.
Оператор называется самоспряжених, если самоспряжених оператору соответствует симметричная матрица 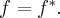
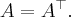
Собственные числа матрицы - это собственные значения оператора и 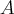
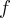
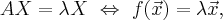
где вектор-столбец 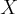 соответствует вектору
соответствует вектору 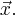
Поскольку между линейными операторами и их матрицами в некотором базисе существует изоморфизм, то свойства собственных чисел и собственных векторов симметричной матрицы являются свойствами собственных чисел и собственных векторов самосопряжённого линейного оператора.
Утверждение. Пусть 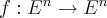 самосопряжённых линейный оператор, тогда все собственные числа
самосопряжённых линейный оператор, тогда все собственные числа 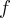 действительны, а собственные векторы, соответствующие различным собственным числам, ортогональны.
действительны, а собственные векторы, соответствующие различным собственным числам, ортогональны.
Итак, если все собственные числа самосопряжённого линейного оператора разные, тогда в евклидовом пространстве существует ортонормированный базис  из собственных векторов этого оператора.
из собственных векторов этого оператора.
Действительно, мы имеем 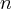 различных действительных собственных чисел, каждому из них соответствует ненулевой собственный вектор. Все собственные векторы между собой ортогональны, нормируем их и получаем орто \ -нор \ -мований базис
различных действительных собственных чисел, каждому из них соответствует ненулевой собственный вектор. Все собственные векторы между собой ортогональны, нормируем их и получаем орто \ -нор \ -мований базис 
Остается вопрос, что происходит, если собственное число как корень характеристического полинома имеет кратность больше единицы? Оказывается, что размерность подпространства собственных векторов, соответствующих собственному числу 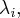 равна кратности корня
равна кратности корня 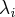 в характеристическом полиноме. Наша задача доказать, что для самосопряжённого оператора существует ортогональный базис из собственных векторов.
в характеристическом полиноме. Наша задача доказать, что для самосопряжённого оператора существует ортогональный базис из собственных векторов.
Напомним, что подпространство 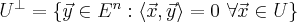 называется ортогональным дополнением подпространства
называется ортогональным дополнением подпространства 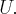 подпространства
подпространства 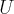 и
и 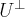 образуют прямую сумму
образуют прямую сумму 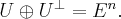
Лема. Пусть 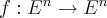 самосопряжённых линейный оператор,
самосопряжённых линейный оператор, 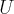 - инвариантный подпространство в отношении этого оператора, то есть
- инвариантный подпространство в отношении этого оператора, то есть 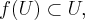 тогда ортогональное дополнение
тогда ортогональное дополнение 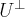 также инвариантным подпространством относительно
также инвариантным подпространством относительно 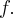
Доказательство. По определениями ортогонального дополнения, инвариантного подпространства и самосопряжённого оператора имеем:
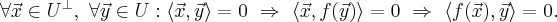
Итак, имеем
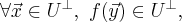
что означает, что 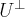 есть инвариантным подпространством относительно
есть инвариантным подпространством относительно 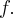
Теорема. Пусть 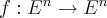 самосопряжённых линейный оператор, тогда в пространстве существует ортонормированный базис из собственных векторов оператора
самосопряжённых линейный оператор, тогда в пространстве существует ортонормированный базис из собственных векторов оператора 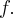
Доведения. Все собственные числа самосопряжённого оператора действительны. Пусть - различные собственные числа кратность которых в характеристическом полиноме может быть больше единицы. 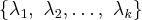

Пусть - соответствующие собственные подпространства (подпространства из собственных векторов). Доказано, что эти подпространства между собой ортогональны, так что они образуют прямую сумму. 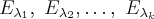
Докажем, что

Предположим обратное

Подпространство 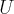 состоит из собственных векторов
состоит из собственных векторов  следовательно он инвариантным подпространство в одноосно этого оператора, по лемме ортогональное дополнение
следовательно он инвариантным подпространство в одноосно этого оператора, по лемме ортогональное дополнение 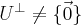 также инвариантным подпространством относительно
также инвариантным подпространством относительно 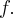 Рассмотрим ограничения
Рассмотрим ограничения 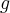 самосопряжённого линейного оператора
самосопряжённого линейного оператора 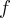 на инвариантный подпространство
на инвариантный подпространство 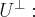
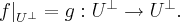
Два оператора 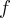 и
и 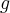 отличаются лишь областью определения. Итак оператор
отличаются лишь областью определения. Итак оператор 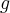 также самосопряжённых, он действует на ненулевом пространстве, следовательно имеет хотя бы одно собственное число
также самосопряжённых, он действует на ненулевом пространстве, следовательно имеет хотя бы одно собственное число 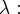
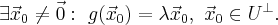
Но 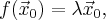 значит
значит 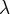 является собственным числом оператора
является собственным числом оператора  а
а 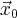 является собственным вектором
является собственным вектором  есть
есть 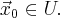 С
С 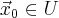 и
и 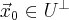 следует, что
следует, что 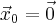 - противоречие. Итак,
- противоречие. Итак,  есть
есть

В каждом из подпространств 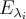 мы можем выбрать ортогональный базис и получить ортогональный базис всего пространства
мы можем выбрать ортогональный базис и получить ортогональный базис всего пространства 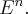 Теорема доказана.
Теорема доказана.
Так что для самосопряжённого оператора существует ортогональный базис из собственных векторов и матрица оператора в этом базисе имеет диагональный вид. Напомним, что матрица перехода 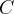 (ее столбики - это координаты новых базисно их векторов) от ортонормированного базиса к ортонормированного является ортогональной:
(ее столбики - это координаты новых базисно их векторов) от ортонормированного базиса к ортонормированного является ортогональной:
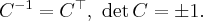
Если - симметричная матрица самосопряжённого линейного оператора в некотором базисе, - матрица перехода к ортонормированного базиса из собственных векторов то в новом базисе мы диагональную матрицу 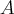
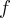
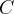

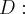
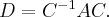
Благодаря изоморфизма между линейными операторами и матрицами мы имеем такую теорему.
Теорема. Для любой симметричной матрицы 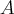 с действительными элементами размера
с действительными элементами размера 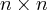 существует ортогональная матрица
существует ортогональная матрица 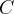 такая, что
такая, что
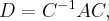
где - диагонально матрица с действительными элементами. 
Или короче, любая симметричная матрица ортогонально подобная диагональной.
Date: 2015-07-01; view: 1376; Нарушение авторских прав