Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Статистическая обработка результатов измерений
|
|
При малом количестве экспериментов (малая выборка) основной задачей является определение с заданной вероятностью интервала, в котором находится средняя арифметическая (математическое ожидание) генеральной совокупности [1]. Под генеральной совокупностью подразумевается выборка из n измерений (единиц) какого-либо свойства, причем n®¥.
Расчет проводится из предположения, что распределение измеряемой величины подчиняется нормальному закону распределения, встречающемуся в технике наиболее часто.
Пусть имеем выборку из n единиц: x1, x2, …xn, где m – среднее арифметическое выборки, s – среднеквадратичное отклонение.
Необходимо определить вероятность Р того, что математическое ожидание а генеральной совокупности располагается в интервале (m ± x) (это доверительный интервал).
Известно, что для нормального закона распределения «нормированное» отклонение, т.е. разность между текущим значением переменной и средней совокупности, отнесенная к среднеквадратичному отклонению, не зависит от среднеквадратичного отклонения, а подчинятся определенному закону распределения.
Нормированное отклонение средних арифметических разных выборок t составляет
,
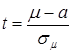где sm – среднеквадратичное отклонение средней арифметической разных выборок.
Известно, что дисперсия средней арифметической выборок в n раз меньше дисперсии переменной, т.е.
.
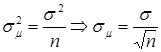Закон распределения нормированного отклонения описывается следующей формулой:
,
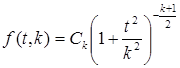где k – число степеней свободы системы (т.е. то количество значений признака, которые могут принять произвольные значения, не изменяя общего уровня, около которого эти значения варьируют). В нашем случае имеем n значений переменной, из них произвольно мы можем назначить n –1 значения с тем, чтобы сохранить величины m и s нашей выборки. Таким образом,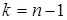 
.
Вероятность того, что t не превзойдет некоторого числа t a, т.е. лежит в интервале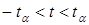 
оценивается интегралом
.
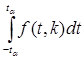Значения этого интеграла при условии, что вероятность события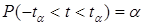 
вычислены и приводятся в приложении 6.
Поскольку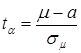 
и мы знаем вероятность Р =a того, что – t a< t < t a, получаем:
.
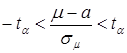Отсюда: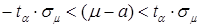 
.
Задав вероятность a, близкую к единице, чтобы можно было считать событие практически достоверным (например, a=0,95), можно найти величину t a. Имея значения a и k и вычислив sm находим произведение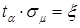 
.
Тогда с вероятностью a математическое ожидание генеральной совокупности а лежит в интервале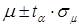 
.
Date: 2015-06-11; view: 383; Нарушение авторских прав