Содержащихся в выбросах в атмосферу группы предприятий 5 page

П.3.4.1.1. Для каждой точки, 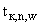, множества 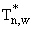определим отрезок наименьшей длины, связывающий эту точку с границей 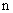-й площадки. В том случае, если такой отрезок не один, выберем из нескольких отрезков тот, который составляет наименьший угол с прямой, проходящей через точку 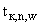и условный центр, 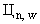, (см. п.П.2.2.4.) расположения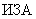 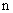-й площадки, выбрасывающих вещества, входящие в набор , .

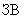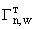П.3.4.1.2. Рассмотрим две прямые, проходящие через точку 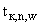, одна из которых (обозначим ее как 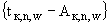) содержит отрезок, построенный в соответствии с п.П.3.4.1., другая (обозначим ее как 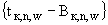) - перпендикулярна прямой 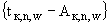в точке .

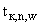П.3.4.1.3. Выберем две другие точки множества 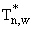: 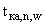и , так, чтобы для них выполнялись следующие требования:

(а) для расстояни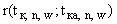й и 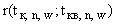от точки 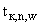до точек 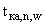и выполняются неравенства:

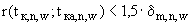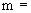( 1, 2, 3) (П.3.12а)

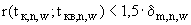
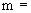( 1, 2, 3) (П.3.12б)

где 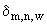- шаг сетки, используемой при построении множества 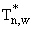(см. п.П.2.3.1-п.П.2.3.3).

(б) расстояние от точки 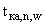до границы 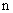-й площадки, измеренное вдоль прямой 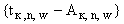, больше длины отрезка, определенного согласно п.П.3.4.1.;

(в1) угол между прямой, проходящей через точк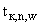и и 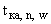(обозначим ее как 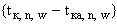) и прямой 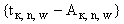, минимален на совокупности точек, для которых выполняются условия (П.3.13а) и (б);

(в2) угол между прямой, проходящей через точк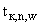и и 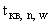(обозначим ее как 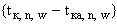), и прямой 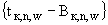минимален на совокупности точек, для которых выполняется условие (П.3.13б).

П.3.4.1.4. Потребуем, чтобы для значений функции 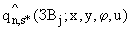в точках 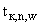, 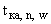и 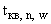выполнялись следующие соотношения:

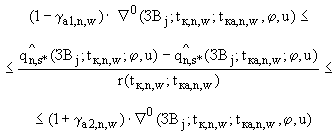(П.3.13а)

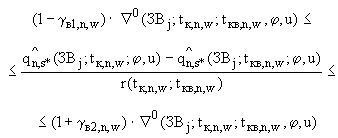(П.3.13б)

Здесь 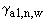, , 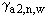, 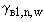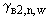определяются с учетом с п.П.3.4.2.2.;

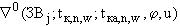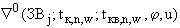и определяются через значения поля приземных концентраций, 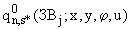, группы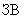 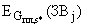, рассчитанных при известных (существующих, планируемых, проектируемых) параметрах выбросов:

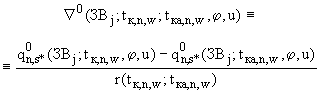(П.3.14а)

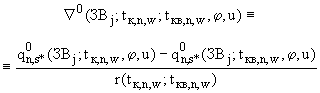(П.3.14б)

П.3.4.2. Потребуем, чтобы, помимо неравенств (П.3.13) для значений функции в каждой точке, 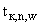, множества 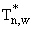выполнялись ограничения:

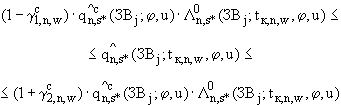(П.3.15)

где 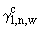, 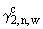определяются с учетом п.П.3.4.2.2.;

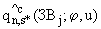- интеграл от функции 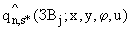по области :

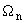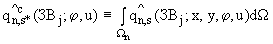(П.3.16)

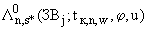отношение значения поля приземных концентраций 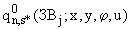, группы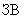 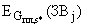, рассчитанного при известных (существующих, планируемых, проектируемых) параметрах выбросов в точке 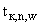к интегралу от этой функции по области :

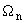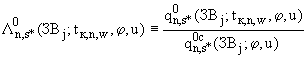(п.3.17)

где 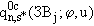- рассчитывается по значениям функции 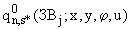в области 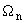аналогично (п.3.16).

П.3.4.2.1. Учитывая те же соображения, что и в п.П.3.3.5., будем вычислять интегралы в (П.3.16) и (П.3.17) аналогично тому, как это предлагалось при вычислении интеграла в (П.3.8).

Отличие от формулы (П.3.8) состоит только в том, что при вычислении интегралов в (П.3.16), (П.3.17) рассматривается не вся область 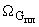, а только область 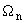, соответствующая функциям 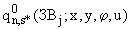и 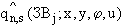. Вследствие этого суммирование в правой части (П.3.8) производится не по всем точкам множества 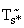, а только по тем из них, которые находятся в области .

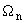П.3.4.2.2. Неотрицательные величины 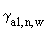, , 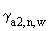, , 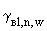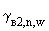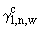и 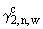характеризуют подобие полей приземных концентраций, , создаваемых выбросами 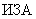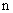-й площадки при известных (существующих, планируемых, проектируемых) значениях их параметров, и тех полей 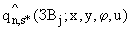, с помощью которых определяетс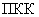я для 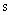*-й группы ).

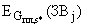Примечания: 1. Целесообразно отметить, что речь идет о похожести характера распределений концентраций на местности (например, их изменения с удалением от площадки), но, ни в коем случае, не о близости значений самих концентраций.

2. Чем меньше значения 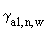, , 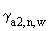, , 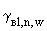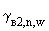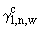и 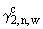тем более похожи поля и .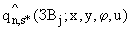

При:

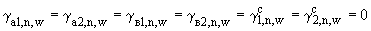(П.3.18)

эти поля отличаются друг от друга только постоянным множителем (т.е. отличается только уровень концентраций, а не характер их распределения на местности). Таким образом слишком малые значения этих величин, слишком "жестко" связывают искомые поля с теми, которые получаются при известных значениях параметров 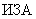, т.е. ограничивают набор возможностей предприятия при достижении .

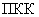3. Слишком большие значения обсуждаемых величин могут привести к тому, что получающиеся в результате функции 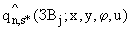будет сложно интерпретировать как поля концентраций, создаваемых выбросами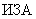 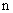-й площадки при реализуемых значениях их параметров.

4. На первых этапах использования настоящих "Рекомендаций..." для величин 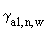, , 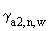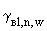и 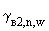может быть рекомендовано использование значений от 0,05 до 0,20.

5. Методы уточнения значени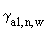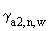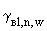й , , и 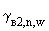в зависимости от положения точки 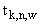будут опубликованы (после их апробации) в качестве дополнений к настоящим "Рекомендациям...".

П.4. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ 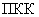ПРЕДПРИЯТИЙ

П.4.1. Для каждой функции 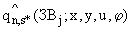( 1,…. ) рассмотрим совокупность ее значений в точках множества 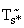, определенного согласно п.П.3.3.5.1. Обозначим, для удобства записи формул, эти значения как:

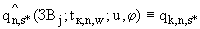( 1,…. ; 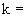1,.... 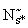) (П.4.1)

где 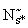- число точек множества .

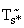П.4.1.1. Тогда условия, которым должна удовлетворять функция 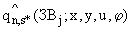, сформулированные в предыдущем разделе, можно записать для 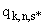так:

Ищется набор чисел 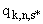( 1,…. ; 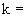1,.... 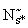), удовлетворяющий следующим требованиям:

<1> При любых 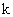и 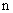из области их изменения верно:

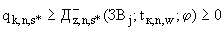(П.4.2а )

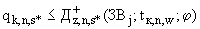(П.4.2а )

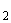<2> При любом значении 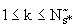выполняются условия (П.3.5):

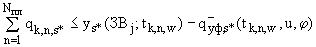(П.4.2б)

<3> Для любых 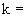1,.... 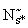и 1,…. выполняются условия (П.3.13а), (П.3.13б) и (П.3.15), записанные в виде:

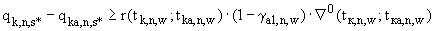(П.4.2в )

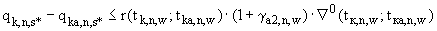(П.4.2в )

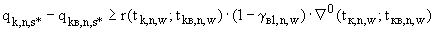(П.4.2г )

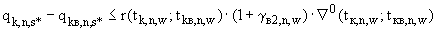(П.4.2г )

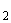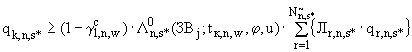(П.4.2д )

(П.4.2д )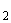

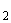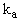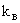В (П.4.2в )-(П.4.2г ) номерам и соответствуют значения функций 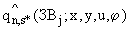в точках 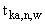и 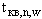, выбираемых из множества 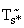в соответствии с п.П.3.4.1.;

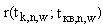и 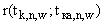- расстояния между соответствующими точками.

В этих соотношениях, для сокращения записи, приняты обозначения:

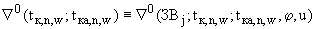
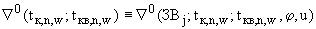
где правые части определяются в соответствии с п.П.3.4.1.4.;

В (П.4.2д) при каждом :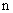

- рассматриваются значения 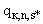, соответствующие точкам 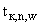, находящимся в области ;

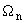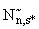- - число точек из множества 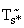, находящихся в области ;

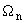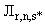- - для каждого значения 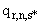рассчитывается как одна треть суммарной площади всех треугольных участков 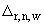, (определенных в соответствии с п.П.3.3.5.2.) в вершине которых находится та точка 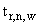, которой соответствует значение :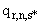

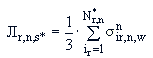(П.4.3)

Здесь 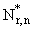- число треугольных участков, принадлежащих последовательности 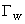(см. п.П.3.3.5.2.), и лежащих в области 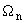, в вершинах которых находится точка ;

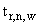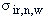- площадь 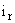-го такого участка, рассчитанная в соответствии с п.П.3.3.5.2.1.

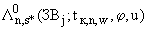- рассчитывается, в соответствии с п.П.3.4.2. как:

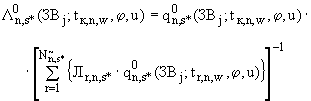(П.4.3а)

где - концентрация группы 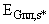(в долях 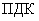), рассчитанная при известных значениях параметров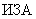 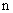-й площадк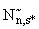и;

и 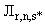те же, что и в (П.4.2д).

Величины 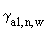, , 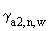, , 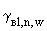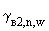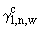и 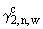в (П.4.2в)-(П.4.2д) определяются с учетом п.П.3.4.2.2.

<4> На искомом наборе чисел 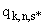( 1,…. ; 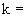1,.... 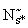) достигается максимум функционала:

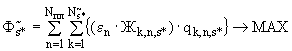(П.4.4)

где 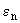- соответствуют описанным в п.П.3.3.4.;

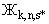- для каждого значения 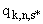рассчитывается как суммарная площадь всех треугольных участков 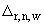, (определенных в соответствии с п.П.3.3.5.2.), в одной из вершин которых находится та точка 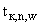, которой соответствует значение :

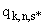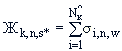(П.4.4а)

Здесь 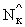- число треугольных участков, принадлежащих последовательности 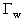(см. п.П.3.3.5.2.), в вершинах которых находится точка ;

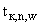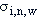- площадь 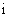-го такого участка, рассчитанная в соответствии с п.П.3.3.5.2.1.

Примечание: В сумме в (П.4.4а), отличие от (П.4.3), учитываются все треугольные участки 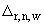, в одной из вершин которых находится точка 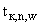, а не только принадлежащие области .

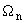П.4.1.2. Сформулированная в п.П.4.1.1. задача является задачей линейного программирования (ЛП). С помощью известных [8] преобразований она может быть приведена к каноническому виду и решена одним из стандартных методов решения таких задач, например, наиболее распространенным, симплекс-методом (см. например, [8]).

П.4.1.3. Решение этой задачи определяет набор из 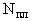векторов:

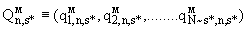(П.4.4)

на которых достигается максимум функционала (П.4.3).

Составляющие 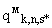каждого вектора 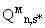определяют на множестве точек 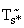значения функции .

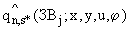Таким образом набор векторов 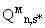определяет на точках множества 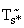набор функций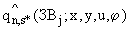 1,…. , оценивающих сверху значения приземных концентраций, которые могут создаваться при выбранных направлении, 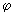, и скорости ветра, 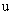, выбросами 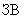определяющей группы, 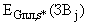(см. п.3.3.2.), из 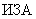каждой, 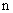-й, площадки из группы взаимовлияющих площадок .

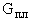Этот набор функций оптимально (в смысле п.П.3.3.4.) учитывает требования к минимизации расходов предприятий при достижении 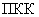и факторы социально-экономической значимости и экологичности технических решений.

П.4.2. Значение предельно допустимого поля 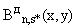для определяющей группы суммации 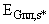в точках множества 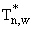(см. п.П.2.3.) рассчитывается как наибольшее по скоростям и направлениям ветра значение функции 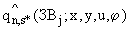в каждой точке:

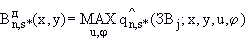(П.4.5)

П.4.3. При установлении 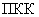предприятий, входящих в группу, 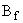, взаимовлияющих предприятий, составляется перечень 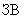(назовем его перечень 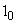), выбрасываемых всеми площадками этих предприятий, входящими в группу, 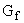, взаимовлияющих площадок (см. П.8.2.1.).

Составляется также перечень 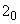, в который входят группы 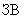с комбинирующимся вредным действием, 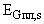(см. примечание к П.8.5.2.), каждая из которых состоит из 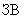, выбрасываемых рассматриваемыми площадками и присутствующих в фоновом загрязнении приземного слоя воздуха.

Date: 2015-06-11; view: 327; Нарушение авторских прав