Представление чисел с плавающей точкой

Математическая запись числа две целых четыре сотых выглядит так 2,04 но возможна и такая запись 0,204×10, или такая 20,4×10^-1, или такая 0,0204×10²... Этот ряд можно продолжать сколь угодно долго. На что вы обратили внимание? - запятая перемещается («плавает») влево или вправо, и, чтобы не изменить значение числа, мы умножаем его на 10 в отрицательной или положительной степени.

Для представления вещественных чисел в памяти ЭВМ используется формат с плавающей точкой. При этом необходимо помнить, что система вещественных чисел представимых в ЭВМ является дискретной и конечной.

В общем случае любое число N, представляемое в форме с плавающей точкой, является произведением двух сомножителей: .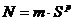

m — мы будем называть мантиссой числа (модуль целой части мантиссы изменяется в диапазоне от 1 до S-1 (включая эти числа), где S- основание системы счисления),

p — целочисленный порядок,

S ¾ основание системы счисления.

Различают нормализованную и экспоненциальную формы записи числа. Если мантисса является правильной дробью, у которой первая цифра после точки отлична от нуля , то число называется нормализованным.

При представлении числа в экспоненциальной форме обязательно присутствует целая часть, содержащая не более одной цифры отличной от нуля, фактически эта форма представления совпадает со стандартной математической формой записи числа.

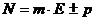
Вещественное число в ПЭВМ представлено в экспоненциальной форме.

Следовательно, при представлении чисел с плавающей точкой необходимо записать в разрядной сетке ЭВМ со своими знаками мантиссу 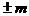и порядок . Знак числа при этом совпадает со знаком мантиссы. Запишем число 314.6789 в экспоненциальной форме:314.6789= 3.1467890000E+2. Число разрядов, выделенных для изображения порядков, определяет диапазон представимых в ЭВМ чисел с плавающей точкой.

Кроме того, этот диапазон зависит также от основания S принятой системы счисления.

Значение произвольного числа вещественного типа представляется в ПЭВМ лишь с некоторой конечной точностью, которая зависит от внутреннего формата вещественного числа, точность представления чисел повышается с увеличением числа разрядов мантиссы.

Для того, чтобы упростить операции над порядками их сводят к действиям над целыми положительными числами путем использования так называемого смещенного порядка, который всегда положителен. смещенный порядок получается путем прибавления к порядку р некоторого целого положительного числа, значение которого зависит от конкретного формата данных.

Десятичная точка подразумевается перед левым (старшим) разрядом мантиссы, но при действиях с числом ее положение смещается влево или вправо в зависимости от двоичного порядка.

Рассмотрим представление чисел в разрядной сетке длиной 4 байта ( так называемая одинарная точность). Изобразим разрядную сетку, состоящую из 32 разрядов и посмотрим, как эти разряды распределены.

0 1 2 3 4 5 6 7 8 … 31

…

знак мантиссы порядок мантисса

Пусть необходимо представить число –13,75 в разрядной сетке с одинарной точностью. Для этого необходимо выполнить следующие действия:

1. перевести число в двоичную систему счисления;

2. представить его в экспоненциальной форме;

3. получить исходный порядок и мантиссу;

4. получить смещенный порядок.

1) 13.75₁₀=1101.11₂

75/100=3/4=3/2²=0.11₂

2) Представим двоичное число 1101.11 в экспоненциальной форме 1101.11=1.10111E+3.

3) Исходный порядок равен 3.

Следует отметить, что целая часть двоичного числа представленного в экспоненциальной форме, всегда равна 1, поэтому в целях экономии разрядов (а следовательно увеличения диапазона представления чисел)целая часть числа не записывается в разрядную сетку.

4) Вычислим смещенный порядок (в формате с одинарной точностью к исходному порядку добавляется число 127)

Pсм=3+127=130=128+2=2⁷+2=10000000₂+102=1000 0010₂

Рсм=10000010₂

Мантисса=.10111₂

Знак числа положительный, следовательно, самый левый разряд равен 0.

0 10000010 10111000000000000000000

знак порядок мантисса

представим полученное число в шестнадцатеричной системе счисления

0100 0001 0101 1100 0000 0000 0000 0000

Итак, мы получили шестнадцатеричное число 415С0000.

Решим обратную задачу.

Значение переменной А Представлено в формате с плавающей точкой в шестнадцатеричной системе счисления А=ВЕ200000. Тип переменной А-single для языка Паскаль. Найти десятичное значение переменной А.

Для решения обратной задачи необходимо выполнить следующие действия:

1) Перевести шестнадцатеричное число в двоичную систему счисления.

2) Выделить знак мантиссы(знак мантиссы совпадает со знаком числа).

3) Выделить смещенный порядок.

4) Вычислить исходный порядок.

5) Записать число, не забыв указать его целую часть, в экспоненциальной форме.

6) Перевести число из экспоненциальной формы в обычную форму записи.

7) Перевести число из двоичной системы счисления в десятичную.

Выполним перечисленные действия.

ВЕ200000=1011 1110 0010 0…0000

1 01111100 0100…0

знак порядок мантисса

Число отрицательное так как левый разряд равен 1.

Вычислим исходный порядок:

Р=Р-127=1111100-127=124-127=-3.

Запишем искомое число в экспоненциальной форме в двоичной системе счисления:

А=-1.01Е-3. Не забывайте указывать целую часть.

Представим искомое число в обычной форме записи в двоичной системе счисления:

А=-1.01Е-3=-0.00101₂=-0.28₁₆=-0.15625.

Операция алгебраического сложения чисел, представленных в форме с плавающей точкой , производится несколько сложнее, чем для чисел, представленных в форме с фиксированной точкой. При выполнении ее сначала выравниваются порядки слагаемых, В результате сравнения порядков порядок меньшего по модулю числа принимается равным порядку большего, а его мантисса сдвигается вправо на число шестнадцатеричных разрядов, равное разности порядков.

В процессе сдвига мантиссы меньшего слагаемого происходит потеря младших разрядов, что вносит определенную погрешность в результат выполнения данной операции.

После выравнивания порядков производится алгебраическое сложение мантисс.

Выполнить самостоятельно:

1) Найти представление десятичного числа А в шестнадцатеричной системе счисления в формате с плавающей точкой. Тип числа single.

А=-357.2265626; А=-0.203125; А=998.46875;

А=–657.4375; А=998.8125; А=-905,34375; А=897.5625

А=637.65625; А=56.53125; А=-4.78125.

2) Значение переменной А представлено в формате с плавающей точкой в шестнадцатеричной системе счисления. Тип переменной А-single для языка Паскаль. Найти десятичное значение переменной А.

А=C455C200; A=43D09400; A=443F9000; A=C2FF8000;

А=44071С00; A=435D2000; А=C401F000; А= С403ЕС00;

A=C3D87400; A=C3D40000; A=C411FA00; A=3F700000.