
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения. 5.1. Комплекты и пропорции
|
|
5.1. Комплекты и пропорции
Завод выпускает 2 изделия U1 и U2. Затраты ресурсов даны в таблице:
| Показатель | Затраты на 1 изделие | Ресурс | |
| U 1 | U 2 | ||
| Трудозатраты | |||
| Сырье |
При производстве 1 единицы изделия U 2 получается 9 ед. скоропортящегося продукта А, который частично используется для производства U 1 в количестве 2 ед. на 1 ед. продукции, а остальная часть уничтожается. Производственные мощности позволяют уничтожить не более 36 ед. продукта А.
Определить оптимальный выпуск U 1 и U 2, если:
1) Изделия входят в комплект в количестве 3 шт. U 1 и 2 шт. Надо максимизировать число комплектов.
Решение
Обозначим: х 1 – выпуск U 1, х 2 – выпуск U 2, х 3 – количество комплектов.
Ограничения на ресурс:
2 х 1 + 3 х 2 £ 60;
20 х 1+ 10 х 2 £ 450.
Ограничения на уничтожение:
Продукт А переработка
9 х 2 - 2 х 1 £ 36.
Ограничение на комплектность:
х 1³ 3∙ х 3
х 2³ 2∙ х 3
Целевая функция: q = х 3 → max.
Полученные ограничения:
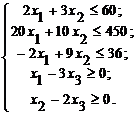
2) Количество изделий U 1 u U 2 должно выпускаться в пропорции 3:2. Максимизировать суммарный выпуск изделий.
Решение
Обозначим х 1 – выпуск U 1, х 2 – выпуск U 2.
Ограничение на ресурс и на уничтожение:
Ограничения на ресурс:
2∙ х 1 + 3∙ х 2 £ 60;
20∙ х 1+ 10∙ х 2 £ 450.
Ограничения на уничтожение:
Продукт А переработка
9∙ х 2 - 2∙ х 1 £ 36.
Ограничение на пропорцию:
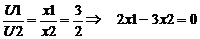 .
.
Целевая функция: q = x 1+ x 2® max.
5.2. Выпуск разнородной продукции на одном оборудовании
Завод выпускает детали А и Б. Цех №1 может изготовить за смену 600 деталей А или 1200 деталей Б. Эти детали затем поступают в цех №2, где за 1 час могут обработать 150 деталей А или 100 деталей Б. Сколько деталей А и Б может выпускать завод за 8-ми часовую смену, чтобы их общее количество было максимально.
Решение
Обозначим: х 1 и х 2 – выпуск деталей А и Б за смену.
Если за смену изготовить 600 деталей А, то на 1 деталь тратиться 1/600 часть смены; на х 1 деталь – надо х 1/600 часть смены. Аналогично на х 2 деталей Б надо х 2/1200 частей смены. Получаем:
 .
.
В цехе №2 на обработку деталей А надо х 1/150 часа, на детали Б – надо х 2/100 часа.
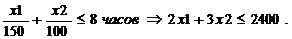
Целевая функция: q = x 1+ x 2® max..
Задание. Исходные данные в приложении 5.
1. Записать целевую функцию;
2. Составить ограничения;
3. Решить задачу с помощью MathCAD;
4. Записать результаты.
Контрольные вопросы и задания.
1. Общий алгоритм разработки модели решения задачи.
2. Что такое область допустимых решений? Как она определяется в задаче?
3. Что такое целевая функция?
4. Что такое нормальный вектор? Каковы его характеристики? Направление нормального вектора.
5. Алгоритм решения в MathCAD.
Date: 2015-07-17; view: 951; Нарушение авторских прав