
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример решения
|
|
Лабораторная работа № 3.
Задача планирования при ограничениях на ресурсы
Цель работы: изучить решение задачи моделирования в условиях ограниченности ресурсов.
Теоретические сведения
У предприятия есть m видов ресурсов (сырьё, оборудование, раб. сила и т. д) каждая в количестве bi единиц i =1,2,... m. Предприятие выпускает n видов продукции. аij - количество единиц i -го ресурса, необходимого для выпуска 1ед. j -й продукции. Прибыль от 1ед. j -ой продукции равна сj $. Продукции j -го вида надо выпускать не менее рj ед.
Определить количество выпускаемой продукции каждого вида, при котором суммарная прибыль максимальна.
При составлении модели оптимизации необходимо выполнить 3 этапа:
1. Определяем значения каких параметров надо найти (что является входными параметрами). Обозначим их х 1, х 2,..., хn.
2. Записываем выражение целевой функции через х 1, х 2,..., хn.
3. Записываем выражение для ограничений через х 1, х 2,..., хn.
Итак:
1. Обозначим хj - объём выпуска j -й продукции (j =1,2,... n).
2. Целевая функция - прибыль. От 1ед. 1-й продукции она равна с 1 $, а от х 1 ед. - с 1∙ х 1. Аналогично от выпуска х 2 ед. 2-ой продукции с 2∙ х 2 и т.д. Суммарная прибыль:
q = с 1∙ х 1 + с 2∙ х 2 +...+ сn ∙ хn → max (1)
3.1. Ограничения на объём выпуска.
Согласно условию
хj ≥ рj (2)
3.2. Ограничения на ресурсы. На одну ед. 1-й продукции надо затратить а 11 ед. 1-го ресурса., а на выпуск х 1 ед. 1-й продукции надо а 11 х 1 1-го ресурса
а 11 х 1 + а 12 х 2 +...+ а1n хn ≤ b 1
………………………….. (3)
аm 1 х 1 + аm 2 х 2 +...+ аmn хn ≤ bm
3.3. По физическому смыслу
хj ≥0 (4)
Замечание. Часто в таких задачах исходные данные имеют различные размерности надо привести всё к одной размерности.
Задание. Исходные данные в приложении 3.
1. Построить систему ограничений.
2. Записать целевую функцию.
3. Решить задачу с помощью MathCAD.
4. Записать результат.
Пример решения
Условие. Автозавод выпускает две модели автомобилей. При производстве одной машины каждой марки затрачивается:
| Марка авто | Квалифицированный труд (часы) | Неквалифицированный труд (часы) | Сырье $ | Прибыль $ |
| Вольво-850 | ||||
| Вольво-940 |
На автозаводе работают 1000 квалифицированных и 900 неквалифицированных рабочих, каждый из которых работает 40 часов в неделю. Затраты на сырье не должны превышать 900 тыс.$ в неделю. Рабочие, осуществляющие отправку автомобилей из цеха, работают по пятидневной рабочей неделе с производительностью 210 автомобилей в день. Какой объем продукции даст максимальную прибыль?
Решение.
1. Определяем входные параметры.
x 1 – количество автомобилей Вольво-850, выпускаемых в неделю
x 2 – количество автомобилей Вольво-940, выпускаемых в неделю
2. Выражение для целевой функции.
 .
.
3. Ограничения.
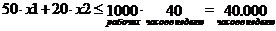 - ограничение по квалифицированному труду;
- ограничение по квалифицированному труду;
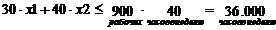 - ограничение по неквалифицированному труду;
- ограничение по неквалифицированному труду;
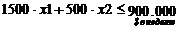 - ограничение по сырью;
- ограничение по сырью;
 - ограничение на доставку авто.
- ограничение на доставку авто.
4. Решение задачи в MathCAD.
Записываем начальные значения искомых переменных и выражение для целевой функции с помощью панели «Арифметика» (рис. 1).
Рис. 1 Панель «Арифметика»
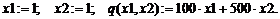
В блоке Given записываем ограничения:
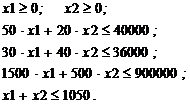
Затем переменным x 1 и x 2 присваиваем минимум (максимум) целевой функции q (x 1 ,x 2) при помощи функции Minimaze (Maximaze) которая находится на панели инструментов (рис. 2):
Рис. 2 Вставка функции
|

Для получения решения записываем 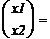 и нажимаем Enter. После этого полученное значение подставляем в выражения для q:
и нажимаем Enter. После этого полученное значение подставляем в выражения для q: 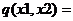 и нажимаем Enter.
и нажимаем Enter.
Полностью решенная задача в MathCAD выглядит следующим образом (рис. 3.):

Рис. 3. Решение задачи
Контрольные вопросы и задания
1. Назовите основные этапы составления модели.
2. В чем состоит отличие целых функций прибыли и затрат?
3. Запишите ограничения на ресурсы в общем виде.
4. В чем смысл ограничений на физическую реализацию?
Date: 2015-07-17; view: 819; Нарушение авторских прав