
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения. Имеется m=2 пункта производства А1, А2, и n=3 пункта потребления В1, В2, В3 некоторого продукта
|
|
4.1. Транспортная задача
Имеется m =2 пункта производства А 1, А 2, и n =3 пункта потребления В 1, В 2, В 3 некоторого продукта. Перевозка из пунктов производства в пункты потребления 1 ед. продукции обходится в некоторую сумму, указанную в тарифной матрице:
| В1 | В2 | В3 | производство | |
| А 1 | ||||
| А 2 | ||||
| потребление |
Известно количество производимого продукта в каждом пункте производства и количество потребляемого в пункте потребления.
Составить план перевозок, при котором затраты минимальны.
Решение.
Нам надо определить, какое количество продукта надо перевозить из каждого пункта производства в каждый пункт потребления.
1. Обозначаем:
x 1 – количество продукта, перевозимого из А 1 в В 1
x 2 – из А 1в В 2;
x 3 – из А 1 в В 3;
x 4 – из А 2 в В 1;
x 5 – из А 2 в В 2;
x 6 – из А 2 в В 3;
2. Общие затраты на перевозку
q = 10 x 1 + 5 x 2 + 6 x 3 + 7 x 4 + 8 x 5 +12 x 6 → min.
3.1 Ограничения на вывоз: из каждого пункта производства нельзя вывезти больше, чем там производят. Из А 1 надо вывезти в В 1 – ч1 ед., в В 2- х 2 ед., в В 3 – х 3 ед. Следовательно: x 1 + x 2 + x 3 ≤ 50. Аналогично для А 2: x 4 + x 5 + x 6 ≤ 40.
3.2 Ограничения на привоз: в каждый пункт потребления нельзя привозить меньше, чем там потребляют.
В 1: х 1+ х 4 ≥ 30;
В 2: х 2+ х 5 ≥ 30;
В 3: х 3+ х 6 ≥ 25.
Замечание. Типичная ошибка: при составлении модели коэффициенты целевой функции матрицы (тариф на перевозку 10, 5 и т. д.) заносят в ограничения. Следует помнить, в ограничениях на ввоз вывоз коэффициенты могут быть равны только 1 или 0, а тарифные коэффициенты встречаются только в целевой функции.
4. Решение с помощью MathCAD.
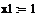 ; ;
|
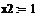 ; ;
|
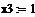 ; ;
|
 ; ;
|
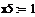 ; ;
|
 ; ;
|
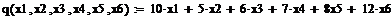 ; ;
|
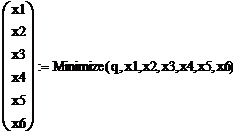
|

|
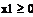 ; ;
|
 ; ;
|
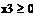 ; ;
|
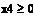 ; ;
|
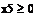 ; ;
|
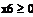 ; ;
|
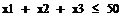 ; ;
|
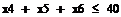 ; ;
|
 ; ;
|
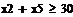 ; ;
|
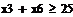 ; ;
|
 . .
|
Date: 2015-07-17; view: 716; Нарушение авторских прав