Точность и количество реализаций модели при зависимом ряде данных

До сих пор мы предполагали, что выходные данные модели образуют ряд значений 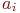, статистически независимых и принадлежащих одному закону распределения. Однако это не всегда так.

Пусть, например, целью статистического моделирования будет определение матожидания времени пребывания заявки в очереди 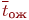одноканальной системы массового обслуживания.

В результате эксперимента с моделью будет получен ряд значений 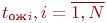, которые заведомо статистически зависимы:

при большом времени ожидания 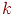-й заявки значение 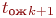, не может быть малым, если обе заявки находились одновременно в очереди. Связь точности оценки 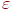, среднего времени ожидания 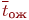с количеством реализаций в этом случае выглядит иначе, чем было рассмотрено ранее. Мы рассмотрим метод определения точности и количества реализаций для статистически зависимых последовательностей - откликов модели, в основе которого лежит так называемый регенеративный анализ.

Допустим, что в результате эксперимента с имитационной моделью получен ряд значений , приведенный в табл. 4.7.

Здесь 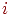- порядковый номер поступающих заявок.

Таблица 4.7. Результаты эксперимента - время ожидания заявки в очереди

…

…

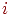
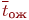
Обратим внимание на то, что заявка 1 застает канал обслуживания свободным: ее время ожидания в очереди равно нулю. Такая же ситуация возникла для заявок 4, 6 и 11. Период занятости и простоя канала обслуживания образуют цикл его работы. В табл. 4.7 можно выделить три таких цикла, в которые входят следующие наборы обслуженных заявок:

• цикл 1 - заявки 1, 2, 3;
• цикл 2 - заявки 4, 5;
• цикл 3 - заявки 6, 7, 8, 9, 10.

Заявка 11 является началом нового цикла 4 и т. д.

Начала каждого цикла неотличимы друг от друга - заявка поступает на обслуживание без ожидания. Говорят так: система восстанавливается (регенерируется) к началу каждого цикла, следовательно, поведение системы в очередном цикле не зависит от ее поведения в предыдущих циклах.

Введем обозначения:

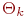- сумма времен ожидания 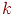-го цикла, ;

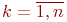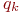- количество заявок, образующих 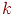-й цикл. Для данных, приведенных в табл. 4.5:

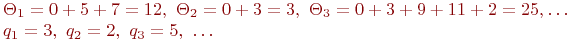
Таким образом, мы получили пары чисел - независимых и одинаково распределенных:

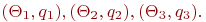
Заметим, что числа 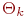и 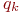между собой зависимы.

Целью дальнейших рассуждений является определение оценки

матожидания времени пребывания заявки в очереди 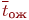, отличающееся от 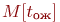на величину не более 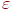при заданной достоверности 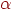. Так как

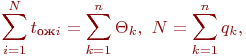
где 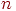- число циклов, то оценка матожидания времени пребывания заявки в очереди определяется так:

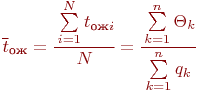
Разделим числитель и знаменатель на число циклов и получим:

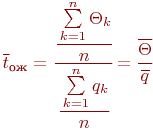
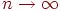В соответствии с центральной предельной теоремой оценка длительности цикла при числе циклов есть случайная величина, распределенная по нормальному закону с математическим ожиданием и дисперсией соответственно:

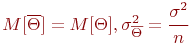
где 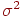- дисперсия, представляющая собой сумму дисперсий зависимых между собой случайных величин и .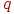

Следовательно, имеет место уже знакомое нам выражение

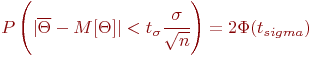
Если 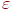- граничное значение ошибки для оценки 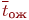, то очевидно граничное значение ошибки для оценки равно .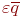

Тогда 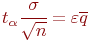. Из этого следует:

Коэффициент 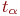, как и ранее, характеризует достоверность оценки 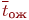и является аргументом функции Лапласа:

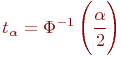
Значения 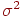и 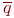до эксперимента неизвестны. Их ориентировочные значения должны быть определены по данным предварительных прогонов модели в количестве 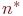реализаций циклов. Обычно .

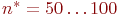Оценку дисперсии 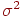обозначим 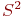. Она вычисляется так:

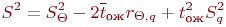
Здесь:

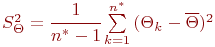- оценка дисперсии ;

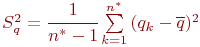- оценка дисперсии ;

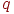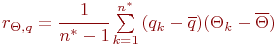- корреляционный момент случайных величин и ;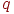

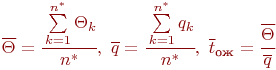
И, наконец, необходимое число циклов будет определено:

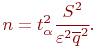
Если окажется , то моделирование продолжается до достижения 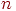циклов. Если же окажется 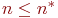, то моделирование заканчивается и, если необходимо, дается оценка достигнутой точности.

Признак конца моделирования: 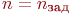или количество обслуженных СМО заявок .

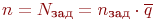Date: 2015-07-17; view: 441; Нарушение авторских прав