Гистограмма

Одной из задач моделирования может быть определение закона распределения вероятностей исследуемой случайной величины и количественных значений его характеристик.

Аналогом, моделью плотности распределения вероятности случайной величины является гистограмма, которую можно построить (аналитически или графически) по данным имитационного моделирования.

Гистограмма (рис. 5.1) строится так.

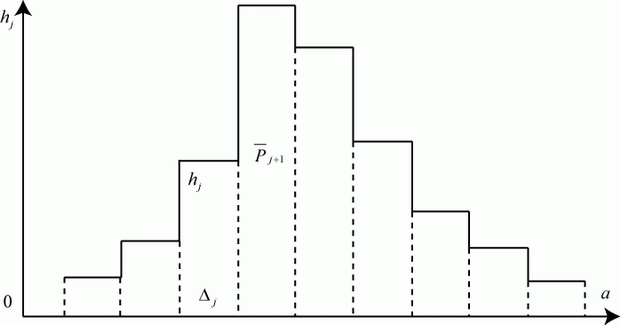
Рис. 5.1. Гистограмма

В результате реализаций модели получен ряд случайных значений исследуемого параметра : 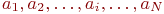. Весь диапазон значений 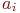разбивается на 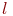интервалов (разрядов). Числовой диапазон каждого интервала обозначим 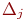, 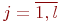. Обычно все числовые диапазоны одинаковые: .

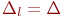Для каждого интервала подсчитываем число значений 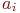, попавших в него - .

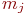На каждом интервале строят прямоугольник с высотой :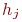

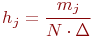
Площадь каждого прямоугольника гистограммы равна относительной частоте :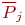

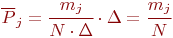
По выбору числа интервалов 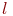существуют разные эмпирические рекомендации, например:

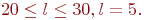
Чем больше и 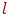, а меньше , тем ближе гистограмма совпадает с некоторым теоретическим распределением. Доказал это Валерий Иванович Гливенко - известный отечественный математик.

На основе очертания гистограммы делается предположение (выдвигается гипотеза) о совпадении полученного эмпирического распределения вероятностей с тем или иным теоретическим - нормальным, экспоненциальным, Вейбулла и т. д. Затем выполняется проверка этой гипотезы с помощью критериев согласия. В курсе высшей математики рассматриваются некоторые (критерий Колмогорова, критерий Смирнова и др.), наиболее популярными считают критерий хи-квадрат - критерий Пирсона, предложенный в 1903 г.

Оценки матожидания и дисперсии можно получить по данным гистограммы:

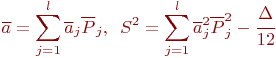
где - среднее значение каждого интервала;

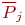- оценка по каждому интервалу;

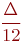- поправка Шеппарда.

Date: 2015-07-17; view: 447; Нарушение авторских прав