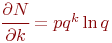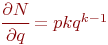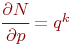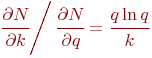Формальный подход к сокращению общего числа прогонов

Рассмотренные способы сокращения общего числа прогонов носят эвристический (субъективный) характер. Они осуществлялись за счет исключения каких-то комбинаций уровней факторов.

Однако во многих случаях исследователь имеет свободу действий в выборе числа факторов 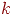, числа уровней 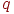и числа прогонов модели в одном наблюдении. Каждый из этих аргументов в конкретной ситуации по-разному влияет на общее число прогонов модели .

Исследуем эти влияния.

Как нам уже известно, общее число прогонов (реализаций) модели равно:

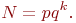
Рассмотрим относительное влияние аргументов 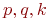на число реализаций .

Сначала нужно получить выражения для вычисления скоростей изменения функции при изменении одного аргумента и неизменных остальных аргументах. Для этого последовательно найдем частные производные первого порядка от функции по этим аргументам:

Теперь сравним попарно полученные производные:

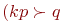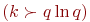Из соотношений 1 и 2 следует: если и , то наибольшее влияние на число оказывает изменение числа уровней .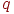

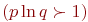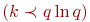Из соотношений 3 и 1 следует: если и , то наибольшее влияние на число оказывает изменение числа факторов .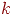

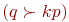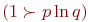Из соотношений 2 и 3 следует: если и , то наибольшее влияние на число оказывает изменение числа реализаций модели на каждом уровне факторов (на каждом наблюдении).

Рассмотренный формальный подход к сокращению числа реализаций не совсем корректен, так как функция общего числа прогонов носит не непрерывный, а дискретный характер. Тем не менее, такой подход применяется с последующим округлением результатов до целых чисел.

Покажем применение формального подхода сокращения реализаций на примере.

Пример 4.4. На вход модели объекта действуют четыре трехуровневых фактора 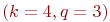. В каждом наблюдении предполагаются восемь прогонов модели . Полный факторный эксперимент потребует 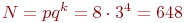прогонов или 81 наблюдение. Такие затраты ресурсов неприемлемы.

Требуется определить, какой из аргументов 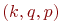следует уменьшить, чтобы достичь наиболее существенного уменьшения числа реализаций .

Решение

Подготовим данные для сравнений:

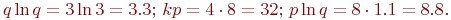
Соблюдается условие:

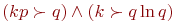, так как .

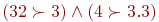Следовательно, наибольшее влияние на изменение оказывает изменение числа уровней .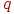

Уменьшим 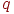на единицу: . В этом случае при ПФЭ потребуется выполнить 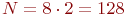прогонов или 16 наблюдений, то есть в пять раз меньше.

Варьирование факторов на двух уровнях встречается часто и решение будет приемлемо, если нет обстоятельств, не устраивающих это решение.

Элементы тактического планирования

Основной задачей тактического планирования является обеспечение результатам компьютерного эксперимента заданных точности и достоверности.

Рассмотрим случай, когда имитационная модель строилась для определения характеристик некоторых случайных величин.

Такими случайными величинами могут быть:

• время обслуживания заявки в СМО;
• численности противоборствующих сторон;
• расход боеприпасов;
• время наработки на отказ технического устройства и др. Из характеристик случайных величин, как правило, интересуют среднее значение (матожидание), дисперсия и характеристика связи случайных величин - коэффициент корреляции.

Характеристику случайной величины будем обозначать греческой буквой .

С помощью имитационного моделирования точное значение определить нельзя, так как число реализаций модели конечно. При конечном числе реализаций модели определяется приближенное значение характеристики. Обозначим это приближение .

Приближенное значение называют оценка соответствующей характеристики: оценкой матожидания, оценкой дисперсии, оценкой коэффициента корреляции.

Точностью характеристики называют величину 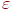в отношении

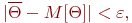
где 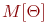- матожидание случайной величины.

Величина 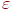представляет собой абсолютное значение ошибки в определении значения искомой характеристики.

Достоверность оценки характеристики называют вероятность 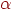того, что заданная точность достигается:

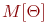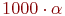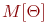Достоверность характеризует повторяемость, устойчивость эксперимента и трактуется так: если для оценки использовать величину , то в среднем на каждые 1000 применений этого правила в случаев величина будет отличаться от на величину меньше .

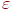В ряде случаев целесообразно пользоваться понятием относительной точности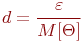

В этом случае достоверность оценки имеет вид:

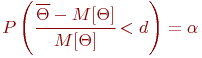
Date: 2015-07-17; view: 411; Нарушение авторских прав