
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Имитационная модель системы массового обслуживания
|
|
Рассмотрим имитационную модель СМО следующего вида:
- многофазная;
- многоканальная;
- с несколькими неоднородными потоками заявок на обслуживание;
- разомкнутая;
- абсолютно надежная;
- с очередями неограниченной емкости на всех фазах обслуживания.
СМО такого вида показана на рис. 3.29.
На рис. 3.29:
 - источники потоков заявок на обслуживание;
- источники потоков заявок на обслуживание;
 - каналы обслуживания;
- каналы обслуживания;
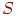 - число фаз;
- число фаз;
 - число каналов в каждой фазе;
- число каналов в каждой фазе;
 - очереди заявок на входах соответствующих фаз.
- очереди заявок на входах соответствующих фаз.
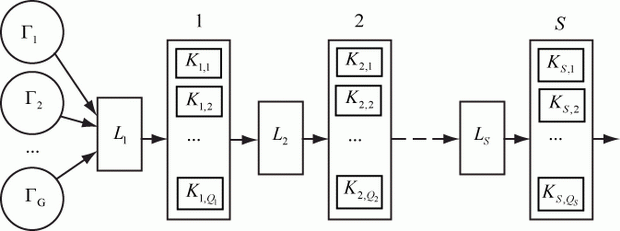
увеличить изображение
Рис. 3.29. Многофазная СМО
Такой СМО может быть, например, сборочный цех радиоэлектронного предприятия. Из нескольких цехов ( ) поступают готовые блоки для сборки изделия. Сначала они поступают на диспетчерские посты, на которых происходит оформление соответствующей документации. После этого блоки направляются на сборочные участки.
) поступают готовые блоки для сборки изделия. Сначала они поступают на диспетчерские посты, на которых происходит оформление соответствующей документации. После этого блоки направляются на сборочные участки.
Диспетчеризация - первая фаза обслуживания.
Сборка изделий - вторая фаза обслуживания.
Затем идет стендовый контроль и регулировка - это третья фаза обслуживания.
Четвертая фаза - приемка готового изделия (например, военная приемка)
Далее может быть упаковка изделия - пятая фаза.
Упакованные изделия поступают в транспортное подразделение для отправки - это шестая фаза.
На каждом из этих шести участков работают инженеры, техники, наладчики, контролеры, упаковщики. В силу различного рода случайностей на входе каждой фазы могут образовываться очереди комплектующих блоков, непроверенных изделий, готовых изделий. А также могут быть простои работников, что в терминах СМО трактуется как очереди свободных каналов.
Вернемся к общей постановке задачи.
Целью моделирования является определение показателей исхода операции массового обслуживания на временном интервале  . Например, оценка относительной пропускной способности СМО, среднее количество заявок в очередях, коэффициент использования каналов в каждой фазе и др.
. Например, оценка относительной пропускной способности СМО, среднее количество заявок в очередях, коэффициент использования каналов в каждой фазе и др.
Проанализируем элементы СМО.
- Входные потоки заявок на обслуживание
Поступление заявок на вход первой фазы - событие активное.
Следовательно, в модели должны быть предусмотрены модули реакции на это событие. Каждый поток обслуживает свой модуль реакции, значит, модулей реакции этого типа должно быть столько, сколько имеется потоков заявок, то есть  . Моменты поступления заявок имитируются соответствующими генераторами (датчиками) случайных интервалов между заявками потоков
. Моменты поступления заявок имитируются соответствующими генераторами (датчиками) случайных интервалов между заявками потоков  .
.
- Каналы обслуживания
Каждый канал имеет два состояния: свободен или занят. Переход в состояние "занят" - событие пассивное, так как определяется поступлением заявки. Переход в состояние "свободен" - событие активное, оно определяется внутренними свойствами канала, например, производительностью. Следовательно, в модели должны быть модули реакции на освобождение каналов. И этих модулей должно быть столько, сколько имеется в нашей СМО каналов:
- Очереди заявок на обслуживание на входах фаз
Эти элементы СМО - пассивные, число состояний неограниченно.
- Очереди свободных каналов в каждой фазе обслуживания
Эти элементы СМО также пассивные, число состояний равно числу каналов в каждой фазе.
- Обобщенный элемент "СМО в целом"
Характеризуется одним активным событием - завершение интервала исследования 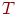 . Следовательно, для обработки этого события в модели предусматривается один специальный модуль реакции.
. Следовательно, для обработки этого события в модели предусматривается один специальный модуль реакции.
Изменения состояний считаем мгновенными. Общее число модулей реакции в рассматриваемой модели должно быть:
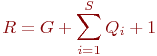
При большом числе входных потоков и каналов обслуживания количество модулей реакции будет значительным, и модель будет труднообозримой, громоздкой. Однако структуру модели можно существенно упростить, назначив однородным активным событиям по одному модулю реакции. Или: освобождение любого канала вызывает обращение к другому общему модулю реакции. Естественно, на входе таких универсальных модулей реакции должен присутствовать блок настройки на конкретное активное состояние объединенной группы.
Строить же общий модуль реакции на освобождение всех каналов СМО нецелесообразно, так как освобождение каналов последней фазы СМО требует действий, заметно отличающихся от тех, которые необходимо выполнить при освобождении каналов не последней фазы.
Таким образом, имитационная модель СМО будет иметь всего четыре модуля реакции:
- модуль реакции на поступление заявки (А);
- модуль реакции на освобождение канала не последней фазы (В);
- модуль реакции на освобождение канала последней фазы (С);
- модуль реакции на завершение интервала исследования
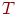 - реакция на изменение состояния обобщенным элементом "СМО в целом".
- реакция на изменение состояния обобщенным элементом "СМО в целом".
Блок-схема имитационной модели СМО состоит из общей части и модулей реакции. Общая часть имеет стандартный вид и была рассмотрена ранее. Структура общей части определяется способом продвижения модельного времени по событиям. Она показана на рис. 3.30.
Блок 1 - установка начальных условий на весь процесс моделирования. Вводятся константы  ,
, 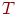 , указываются число источников заявок, число каналов. Счетчик числа реализаций
, указываются число источников заявок, число каналов. Счетчик числа реализаций 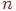 устанавливается в нуль (или в
устанавливается в нуль (или в  - в зависимости от того, как организован счет реализаций модели). Указываются данные планирования эксперимента с моделью и др.
- в зависимости от того, как организован счет реализаций модели). Указываются данные планирования эксперимента с моделью и др.
Блок 2 - установка начальных условий на очередную реализацию модели. Текущее время, счетчики числа поступивших и обслуженных заявок устанавливаются в нуль. Каналы обслуживания и очереди к ним устанавливаются в исходные состояния (установки исходных состояний определяются требованиями к исследованию) и др.
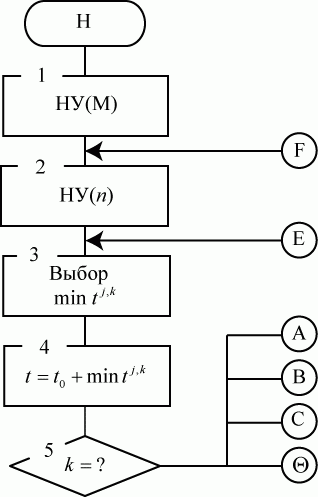
Рис. 3.30. Блок схема имитационной модели СМО
Наборы исходных данных 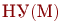 и
и 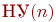 определяются конкретным назначением моделируемой СМО и характером последующих экспериментов.
определяются конкретным назначением моделируемой СМО и характером последующих экспериментов.
Блоки 3, 4 реализуют продвижение времени по событиям.
Блок 5 - выбор модуля реакции. В зависимости от индекса 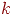 пространственно временной точки
пространственно временной точки  передает управление соответствующему модулю реакции -
передает управление соответствующему модулю реакции - 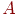 ,
, 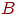 ,
,  или
или  .
.
В рассматриваемой модели элементы СМО имеют только два состояния, одно из которых является начальным. Поэтому индекс 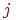 не имеет смысла.
не имеет смысла.
Рассмотрим состав и функционирование модулей реакции.
Допустим, что в рассматриваемый момент времени свершилось активное событие - поступление заявки от одного из источников. Блок 5 передает управление модулю реакции А.
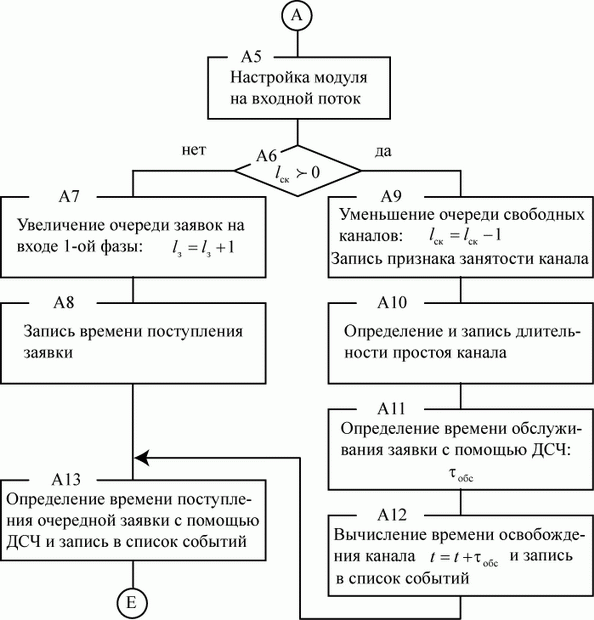
Блок-схема алгоритма модуля реакции 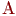 приведена рис. 3.31.
приведена рис. 3.31.
Блок А5 - блок настройки. Обеспечивает доступ к ДСЧ, ячейкам и т. д. модуля, предназначенным для обслуживания конкретного потока заявок, которому принадлежит поступившая заявка.
увеличить изображение
Рис. 3.31. Блок-схема алгоритма модуля реакции А
Блок А6 - проверка наличия свободных каналов первой фазы. Количество свободных каналов в очереди обозначено: 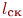 .
.
Если все каналы заняты 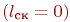 , управление передается блоку А7. Если свободные каналы есть
, управление передается блоку А7. Если свободные каналы есть 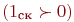 , управление передается блоку А9.
, управление передается блоку А9.
Блок А7 - размещение поступившей заявки в соответствующей очереди первой фазы 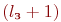 . Текущее содержимое этой очереди обозначено как
. Текущее содержимое этой очереди обозначено как 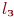 .
.
Блок А8 - запоминание времени постановки заявки в очередь и передача управления блоку А13.
Правая ветвь алгоритма (см. рис. 3.30) выполняет действия, связанные с постановкой заявки на обслуживание.
Блок А9 - имитация загрузки одного из свободных каналов поступившей заявкой. Очередь свободных каналов уменьшается на 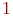 (
(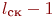 ). Выбранному каналу присваивается признак занятости -
). Выбранному каналу присваивается признак занятости - 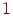 . У свободных каналов этот признак равен
. У свободных каналов этот признак равен 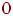 .
.
Блок А10 - определение и запоминание длительности простоя канала. Накопление времени простоя необходимо, например, для определения коэффициента занятости канала на интервале исследования.
Блок А11 -имитация времени обслуживания заявки.
Случайное время обслуживания 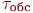 формируется обращением к соответствующему датчику случайных чисел.
формируется обращением к соответствующему датчику случайных чисел.
Блок А12 - прогноз времени окончания обслуживания 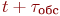 и занесение новой пространственно-временной точки в список событий.
и занесение новой пространственно-временной точки в список событий.
Блок А13 - прогноз момента времени поступления очередной заявки. Соответствующий датчик случайных чисел выдает длительность случайного временного интервала между заявками данного типа. Момент поступления очередной заявки вычисляется как 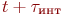 . Полученная таким образом пространственно-временная точка заносится в список событий.
. Полученная таким образом пространственно-временная точка заносится в список событий.
Управление передается в точку Е - блоку 3 для определения очередного ближайшего события.
Если очередным ближайшим событием окажется освобождение канала не последней фазы, то блок 5 передает управление модулю реакции В, имитирующему действия в СМО при свершении этого активного события.
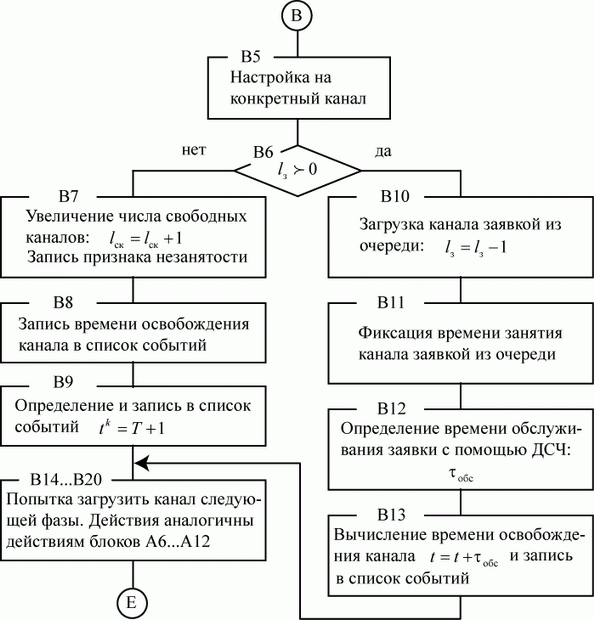
Блок-схема алгоритма модуля реакции В представлена на рис. 3.32.
Модуль В имеет две функции. Во-первых, попытаться загрузить освободившийся канал заявкой из очереди на входе фазы, в которой находится освободившийся канал. Во-вторых, имитировать продвижение заявки, освободившей канал, в следующую фазу обслуживания.
увеличить изображение
Рис. 3.32. Блок-схема алгоритма модуля реакции В
Блок В5 -настройка модуля на освободившийся канал конкретной фазы.
Каждая фаза обслуживания имеет свою очередь заявок на входе, свою очередь свободных каналов и, возможно, свои датчики случайных чисел. Поэтому не будем вводить для них новые обозначения, оставим те, которые были использованы при описании модуля А.
Блок В6. Проверка: есть ли в очереди на входе фазы заявки, ожидающие обслуживания (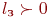 )? Если есть, то освободившийся
)? Если есть, то освободившийся
канал должен быть немедленно загружен (блоки 10… 13). Если нет, то канал должен быть переведен в режим ожидания (блоки В7…В9).
Блок В7. Очередь свободных каналов увеличивается на 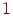 (
(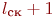 ). Признак занятости канала устанавливается в нуль.
). Признак занятости канала устанавливается в нуль.
Блок В8. Запоминание момента освобождения канала.
Блок В9. Перевод освободившегося канала в пассивное состояние. Для этого пространственно-временной точке 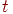 , относящейся к освободившемуся каналу, присвоить значение времени,
, относящейся к освободившемуся каналу, присвоить значение времени,
превышающего интервал исследования 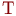 , то есть
, то есть  . Это значение
. Это значение 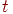 заносится в список событий. Управление передается блоку В14.
заносится в список событий. Управление передается блоку В14.
Блоки В14…В20 моделируют размещение заявки, освободившей канал, в следующей фазе обслуживания. Функции и взаимные связи этих блоков аналогичны блокам А6 … А12, рассмотренным ранее:
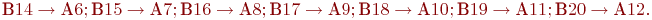
Блок 20 передает управление блоку 3 для идентификации очередного активного события. Этим событием может быть поступление заявки от какого-либо источника на вход первой фазы или окончание обслуживания заявки каким-либо каналом. В этих случаях управление будет снова передано модулям реакции 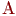 или
или 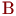 .
.
Если же очередным активным событием окажется освобождение канала последней фазы, то управление передается модулю реакции С (рис. 3.33).
Блок С5 - настройка на соответствующий канал последней фазы. Аналогичен блоку В5.
Блоки С6…С13 - загрузка освободившегося канала ожидающей заявкой, если таковая есть на входе последней фазы. Функции и взаимосвязи блоков аналогичны блокам В6…В13. Блок С6 соответствует блоку В6, блок С7 - блоку В7 и т. д. по одинаковым номерам.
Блок С14 формирует числовые атрибуты заявок, покидающих СМО. Такими атрибутами могут быть: суммарное время обслуживания заявки на всех фазах, суммарное время ожидания в очередях, число обслуживаний без ожидания и др. Атрибуты запоминаются и управление передается блоку 2.

Рис. 3.33. Блок-схема алгоритма модуля реакции С
Если очередное значение 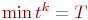 , что означает окончание интервала исследования работы СМО, управление передается модулю реакции
, что означает окончание интервала исследования работы СМО, управление передается модулю реакции  (рис. 3.34).
(рис. 3.34).
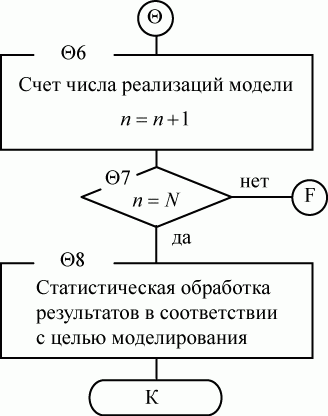
Рис. 3.34. Блок-схема алгоритма модуля реакции \Theta
Построить имитационную модель с продвижением времени можно и по-другому. Однако рассмотренная структура модели обладает важными достоинствами:
- Моделирующий алгоритм нагляден и прост, что существенно упрощает программирование и, особенно, отладку модели, а также изучение готовых моделей.
- Рассмотренная структура алгоритма позволяет параллельно разрабатывать модель по отдельным модулям и, следовательно, сокращать время на ее создание.
Облегчены корректировка и развитие модели. Например, в рассмотренной модели СМО легко учесть выход из строя и восстановление каналов обслуживания. Для этого надо добавить два модуля реакции: один - на возникновение отказа, другой - на восстановление работоспособности. Оба эти события рассматриваются как активные, если неисправность возникает из-за внутренних дефектов оборудования, а восстановление является результатом усилий обслуживающего персонала, входящего в состав СМО.
Вопросы для самоконтроля
- Что такое имитационная статистическая модель? Сравните ее с аналитической моделью.
- Назначение датчиков случайных чисел (генераторов) в имитационном моделировании.
- Принцип формирования случайных чисел в алгоритмических датчиках случайных чисел.
- Почему случайные числа, формируемые в компьютере, являются псевдослучайными квазиравномерными?
- Формирование случайных величин с произвольными законами распределения вероятностей методом обратной функции.
- Формирование равномерно распределенных случайных чисел на произвольном отрезке
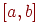 .
. - Формирование нормально распределенных случайных чисел с произвольными значениями
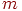 и
и 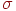 .
. - Найти методом обратной функции процедуру розыгрыша непрерывной случайной величины, распределенной по закону Ре-лея, заданного плотностью вероятности
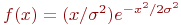 при
при 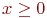 ;
; 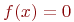 при
при 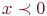 .
. - Найти процедуру розыгрыша случайной величины, распределенной по закону Вейбулла, заданного плотностью вероятности
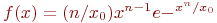 при
при 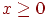 ;
; 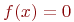 при
при 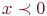 .
. - Создать программу мультипликативного датчика равномерно распределенных случайных чисел для 64-разрядной сетки:
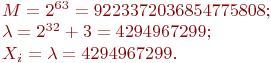
Определить период повторения случайных чисел.
- Усовершенствуйте алгоритм имитационной модели (рис. 3.5) так, чтобы можно было определять не только оценку математического ожидания вероятности поражения объекта, но оценку математического ожидания расхода ракет.
- Способ моделирования единичных событий.
- Способы моделирования полной группы несовместных событий.
- Три способа моделирования совместных независимых событий.
- Моделирование совместных зависимых событий.
- Стационарный и нестационарный случайные процессы.
- Эргодический и неэргодический случайные процессы.
- Способы продвижения модельного времени в имитационной модели.
- Какие виды времени различают при имитационном моделировании?
- Что понимается под распределенным имитационным моделированием? Сравните его с последовательным имитационным моделированием.
- Что значит квазипараллельное моделирование?
- Модель противоборства, назначение блоков. Признаки окончания одной реализации.
- Поясните прием моделирования противоборства двух сторон методом "блуждания по решетке".
- Понятие активного и пассивного элемента в модели СМО.
- Блок-схема имитационной модели СМО.
- Модули реакции в модели СМО.
- Достоинства структуры модели СМО.


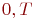 ).
). 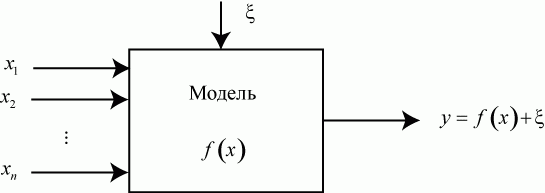 Рис. 4.1. Кибернетическое представление эксперимента
На рис. 4.1:
Рис. 4.1. Кибернетическое представление эксперимента
На рис. 4.1:
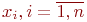 - входные переменные, факторы;
- входные переменные, факторы;
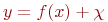 - выходная переменная (реакция, отклик);
- выходная переменная (реакция, отклик);
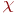 - ошибка, помеха, вызываемая наличием случайных факторов;
- ошибка, помеха, вызываемая наличием случайных факторов;
 - оператор, моделирующий действие реальной системы, определяющий зависимость выходной переменной
- оператор, моделирующий действие реальной системы, определяющий зависимость выходной переменной 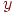 от факторов
от факторов  .
Иначе:
.
Иначе: 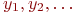 В дальнейшем будем говорить об одном отклике
В дальнейшем будем говорить об одном отклике 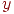 .
Второй проблемой стратегического планирования является выбор (определение) существенных факторов и их сочетаний, влияющих на работу моделируемого объекта. Факторами могут быть питающие напряжения, температура, влажность, ритмичность поставок комплектующих и многое другое. Обычно число факторов велико и чем меньше мы знакомы с моделируемой системой, тем большее, нам кажется, число их влияет на работу системы. В теории систем приводится так называемый принцип Парето:
.
Второй проблемой стратегического планирования является выбор (определение) существенных факторов и их сочетаний, влияющих на работу моделируемого объекта. Факторами могут быть питающие напряжения, температура, влажность, ритмичность поставок комплектующих и многое другое. Обычно число факторов велико и чем меньше мы знакомы с моделируемой системой, тем большее, нам кажется, число их влияет на работу системы. В теории систем приводится так называемый принцип Парето:
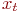 , где индекс
, где индекс 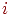 указывает номер (тип) фактора. Встречаются и такие обозначения факторов:
указывает номер (тип) фактора. Встречаются и такие обозначения факторов: 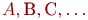 и т. д.
Третьей проблемой стратегического планирования является выбор значений каждого фактора, называемых уровнями фактора.
Число уровней может быть два, три и более. Например, если в качестве одного из факторов выступает температура, то уровнями могут быть: 80o С, 100o С, 120o С.
Для удобства и, следовательно, удешевления эксперимента число уровней следует выбирать поменьше, но достаточное для удовлетворения точности и достоверности эксперимента. Минимальное число уровней - два.
С точки зрения удобства планирования эксперимента целесообразно устанавливать одинаковое число уровней у всех факторов. Такое планирование называют симметричным.
Анализ данных эксперимента существенно упрощается, если назначить уровни факторов, равноотстоящие друг от друга. Такой план называется ортогональным. Ортогональность плана обычно достигают так: две крайние точки области изменения фактора выбирают как два уровня, а остальные уровни располагают так, чтобы они делили полученный отрезок на две части.
Например, диапазон питающего напряжения 30…50 В на пять уровней будет разбит так: 30 В, 35 В, 40 В, 45 В, 50 В.
Эксперимент, в котором реализуются все сочетания уровней всех факторов, называется полным факторным экспериментом (ПФЭ).
План ПФЭ предельно информативен, но он может потребовать неприемлемых затрат ресурсов.
Если отвлечься от компьютерной реализации плана эксперимента, то число измерений откликов (реакций) модели
и т. д.
Третьей проблемой стратегического планирования является выбор значений каждого фактора, называемых уровнями фактора.
Число уровней может быть два, три и более. Например, если в качестве одного из факторов выступает температура, то уровнями могут быть: 80o С, 100o С, 120o С.
Для удобства и, следовательно, удешевления эксперимента число уровней следует выбирать поменьше, но достаточное для удовлетворения точности и достоверности эксперимента. Минимальное число уровней - два.
С точки зрения удобства планирования эксперимента целесообразно устанавливать одинаковое число уровней у всех факторов. Такое планирование называют симметричным.
Анализ данных эксперимента существенно упрощается, если назначить уровни факторов, равноотстоящие друг от друга. Такой план называется ортогональным. Ортогональность плана обычно достигают так: две крайние точки области изменения фактора выбирают как два уровня, а остальные уровни располагают так, чтобы они делили полученный отрезок на две части.
Например, диапазон питающего напряжения 30…50 В на пять уровней будет разбит так: 30 В, 35 В, 40 В, 45 В, 50 В.
Эксперимент, в котором реализуются все сочетания уровней всех факторов, называется полным факторным экспериментом (ПФЭ).
План ПФЭ предельно информативен, но он может потребовать неприемлемых затрат ресурсов.
Если отвлечься от компьютерной реализации плана эксперимента, то число измерений откликов (реакций) модели 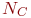 при ПФЭ равно:
при ПФЭ равно:
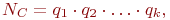 где
где 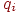 - число уровней
- число уровней 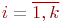 ;
; 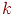 - число факторов эксперимента.
Величина
- число факторов эксперимента.
Величина  . Тогда для симметричного ПФЭ общее число
. Тогда для симметричного ПФЭ общее число 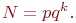 Пример 4.1. Планируется провести компьютерный эксперимент, в котором на отклик модели влияют три фактора. Для каждого фактора установлены три уровня. Требования по точности и достоверности требуют 6000 прогонов модели на каждом уровне (для каждого наблюдения). Время одного прогона модели равно 2 с.
Оценить затраты времени на проведение компьютерного эксперимента.
Решение
Исходные данные:
Пример 4.1. Планируется провести компьютерный эксперимент, в котором на отклик модели влияют три фактора. Для каждого фактора установлены три уровня. Требования по точности и достоверности требуют 6000 прогонов модели на каждом уровне (для каждого наблюдения). Время одного прогона модели равно 2 с.
Оценить затраты времени на проведение компьютерного эксперимента.
Решение
Исходные данные:  ,
, 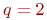 ,
, 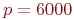 ,
, 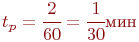 .
Число прогонов модели:
.
Число прогонов модели: 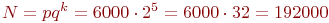 .
Затраты времени:
.
Затраты времени: 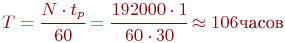 .
Ранее на рис. 4.1 был показан оператор преобразования - математическая модель процесса
.
Ранее на рис. 4.1 был показан оператор преобразования - математическая модель процесса 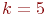 ,
, 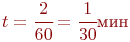 затраты времени на проведение компьютерного эксперимента ожидаются в 106 часов. Поэтому актуальной становится проблема более или менее обоснованного сокращения плана эксперимента (числа наблюдений). Способов сокращения плана и, следовательно, уменьшения затрат времени на проведение экспериментов, много, но все они, в конечном счете, основаны на пренебрежении эффектами парных, тройных и более взаимодействий факторов. Естественно, это снижает точность моделирования, но во многих случаях допустимо.
Рассмотрим несколько примеров.
Пример 4.2. Необходимо провести эксперимент с моделью, имеющей три двухуровневых фактора, с целью построения математической модели ("вторичной модели") процесса в виде:
затраты времени на проведение компьютерного эксперимента ожидаются в 106 часов. Поэтому актуальной становится проблема более или менее обоснованного сокращения плана эксперимента (числа наблюдений). Способов сокращения плана и, следовательно, уменьшения затрат времени на проведение экспериментов, много, но все они, в конечном счете, основаны на пренебрежении эффектами парных, тройных и более взаимодействий факторов. Естественно, это снижает точность моделирования, но во многих случаях допустимо.
Рассмотрим несколько примеров.
Пример 4.2. Необходимо провести эксперимент с моделью, имеющей три двухуровневых фактора, с целью построения математической модели ("вторичной модели") процесса в виде:
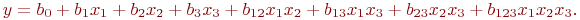 Уравнение имеет восемь коэффициентов, следовательно, достаточно провести восемь наблюдений. Это уравнение соответствует
ПФЭ типа
Уравнение имеет восемь коэффициентов, следовательно, достаточно провести восемь наблюдений. Это уравнение соответствует
ПФЭ типа 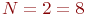 .
Полный факторный эксперимент дает возможность определить не только коэффициенты
.
Полный факторный эксперимент дает возможность определить не только коэффициенты 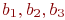 , соответствующие так называемым линейным эффектам (их также называют главными), но и коэффициенты
, соответствующие так называемым линейным эффектам (их также называют главными), но и коэффициенты 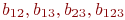 , соответствующие всем эффектам взаимодействия факторов, а также свободный член
, соответствующие всем эффектам взаимодействия факторов, а также свободный член 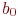 .
Эффекты взаимодействия двух и более факторов проявляются, если влияние каждого из них на отклик зависит от уровней, на которых установлены другие факторы.
Теперь допустим, что число наблюдений в эксперименте, равное восьми, неприемлемо и план надо сократить.
Вполне естественно предположить, что эффекты взаимодействия оказывают на реакцию системы существенно меньшее влияние, чем линейные, или даже отсутствуют вовсе, если факторы обладают свойством независимости.
Исключим их и тогда модель процесса (уравнение отклика, уравнение реакции, "вторичная модель") принимает вид:
.
Эффекты взаимодействия двух и более факторов проявляются, если влияние каждого из них на отклик зависит от уровней, на которых установлены другие факторы.
Теперь допустим, что число наблюдений в эксперименте, равное восьми, неприемлемо и план надо сократить.
Вполне естественно предположить, что эффекты взаимодействия оказывают на реакцию системы существенно меньшее влияние, чем линейные, или даже отсутствуют вовсе, если факторы обладают свойством независимости.
Исключим их и тогда модель процесса (уравнение отклика, уравнение реакции, "вторичная модель") принимает вид:
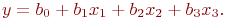 Теперь число неизвестных коэффициентов
Теперь число неизвестных коэффициентов 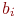 сократилось вдвое и число необходимых наблюдений для их определения стало равно четырем.
Что это за наблюдения?
Четыре наблюдения достаточны для проведения ПФЭ при двух
факторной модели
сократилось вдвое и число необходимых наблюдений для их определения стало равно четырем.
Что это за наблюдения?
Четыре наблюдения достаточны для проведения ПФЭ при двух
факторной модели  . Этими факторами, например, могут быть
. Этими факторами, например, могут быть 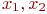 или другая двухфакторная комбинация из трех факторов.
Уровни третьего фактора
или другая двухфакторная комбинация из трех факторов.
Уровни третьего фактора 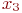 получают из первых двух с помощью, так называемого генерирующего соотношения:
Поскольку факторы двухуровневые, то в общем виде уровни принято обозначать так:
получают из первых двух с помощью, так называемого генерирующего соотношения:
Поскольку факторы двухуровневые, то в общем виде уровни принято обозначать так:
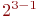 . План приведен в табл. 4.1.
. План приведен в табл. 4.1.
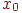
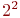
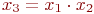
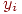
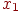
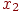
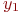
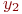
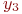
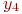
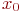 обеспечивает вычисление свободного члена
обеспечивает вычисление свободного члена 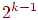 , получая четверть реплики
, получая четверть реплики 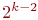 и более мелкие реплики.
и более мелкие реплики.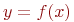 нужно проверять на адекватность, используя для этого "сэкономленные" наблюдения.
нужно проверять на адекватность, используя для этого "сэкономленные" наблюдения.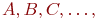 а уровни - индексами при соответствующих факторах:
а уровни - индексами при соответствующих факторах: 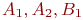 .
.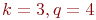 .
.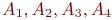 - уровни доминирующего фактора
- уровни доминирующего фактора 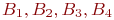 - уровни фактора
- уровни фактора  ;
;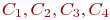 - уровни фактора
- уровни фактора 

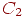
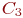
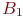
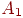
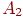
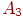
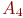
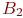
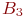
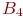
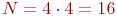 . В полном плане их было бы
. В полном плане их было бы  . Сокращение произошло за счет исключения некоторых комбинаций:
. Сокращение произошло за счет исключения некоторых комбинаций: 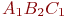 ,
, 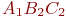 и др.
и др.