Модель противоборства как процесс блуждания по решетке

Итак, чтобы построить имитационную модель, надо скопировать и описать в виде программы элементарные действия процесса и соединить их в нужной последовательности. Такое прямолинейное моделирование, в общем, понятно и естественно.

Однако, иногда можно увидеть совсем неожиданную аналогию (структурную или функциональную) между исследуемым процессом и некоторым другим, на первый взгляд ничего не имеющим общего с оригиналом. Имитационная модель этого нового процесса может оказаться проще и, тем не менее, позволит определить искомые характеристики.

В частности, для исследования процесса противоборства двух сторон таким "дублером" может быть процесс "блуждания частицы по решетке".

Рассмотрим, как перемещение некоторого объекта по решетке становится аналогом, моделью противоборства двух сторон, если целью моделирования является определение оценок численностей сторон в конце операции - интервала исследования.

Противоборствуют две стороны: 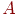и .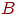

Первоначальные численности сторон: 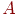и .

Текущие численности сторон: и ; , .

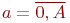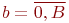Время "жизни" каждого средства случайно, имеет экспоненциальное распределение с параметрам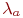и и 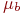сторон 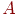и .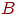

Обе стороны образуют единую систему 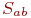. В ходе боя численности сторон изменяются (уменьшаются) или остаются неизменными. Мы это трактуем как переход системы из одного состояния в другое: 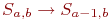или 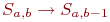и т. д.

Граф состояний такой системы имеет вид двумерной целочисленной решетки с однонаправленными связями. Переходу системы из одного состояния в другое можно поставить в соответствие случайное блуждание некоторой частицы по решетчатой структуре. Отсюда и название моделирующей абстракции.

Граф состояний приведен на рис. 3.26.

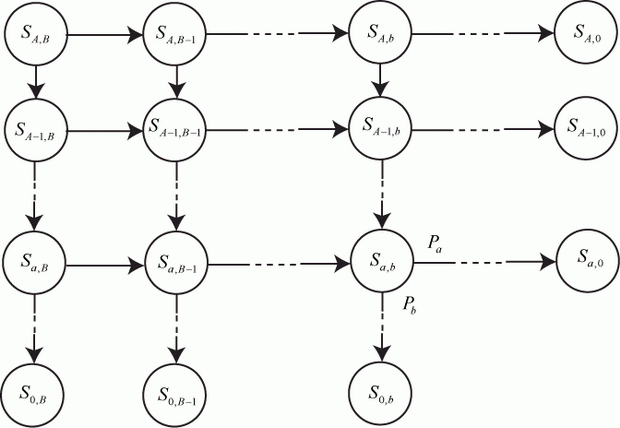
увеличить изображение
Рис. 3.26. Граф состояний моделируемой системы противоборства Исходное состояние системы S_{a,b}.

Стороны ведут взаимоуничтожающий огонь. В предположении ординарности потока событий, переводящего систему из одного состояния в другое, система из состояния 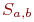может перейти только лишь в состояние 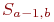или 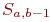(или остаться в прежнем состоянии 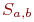). Очевидно, направления переходов в графе - решетке только вправо или вниз.

Процесс противоборства заканчивается при полном уничтожении средств одной из сторон, т. е. при переходе в состояние 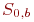или 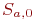, а также по окончании временного интервала исследования 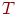. Так заканчивается одна, 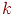-я реализация процесса противоборства. Зафиксировав остатки средств сторон 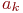и 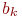и усреднив их за реализаций, найдем решение поставленной задачи - определение оценок численностей сторон на момент окончания операции.

Продвижение времени в модели - фиксированными шагами 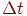. Величина 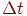такова, чтобы на этом временном участке происходило не более одного события.

Суммарные интенсивности огня сторон 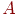и зависят от численностей их боеспособных средств и равны 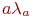и.

Следовательно, вероятности уничтожения одного из средств (перехода системы в очередное состояние) равны:

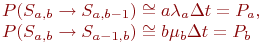
Эти приближенные равенства тем точнее, чем меньше .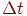

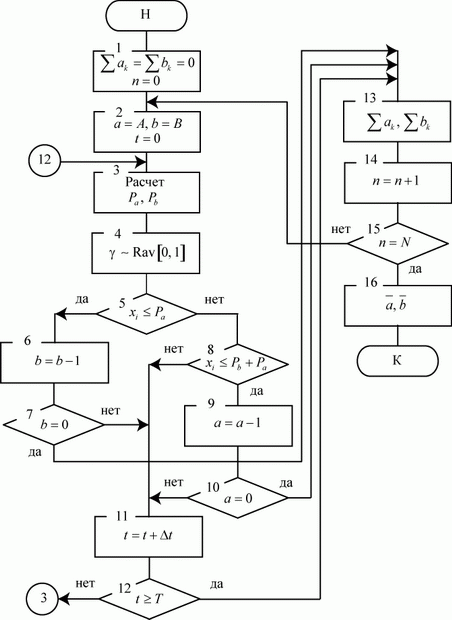
Блок схема алгоритма ИМ противоборства двух сторон, построенная способом "блуждания частицы по решетке" представлена на рис. 3.27.

Блоки 1 и 2 - установка начальных условий на весь процесс моделирования и на каждую очередную реализацию.

Блок 3 - расчет вероятностей и .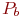

Блоки 4…10 - определение исхода противоборства на очередном временном отрезке 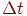. Если 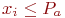, то свершилось событие 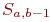, иначе - проверка условия 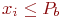? Если это условие выполняется, то свершилось событие 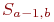, если не выполняется, то пораженных средств не оказалось. Вероятность этого события равна .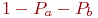

Блоки 11… 16 аналогичны соответствующим блокам предыдущей имитационной модели противоборства двух сторон (см. рис. 3.22).

Сравним обе рассмотренные модели противоборства двух сторон.

Последняя заметно проще. Упрощение связано с тем, что в ней не моделируется поведение каждого отдельного средства, а рассматривается поведение системы в целом.

Однако, первую модель несложно развить, например, учесть неоднородность средств в каждой группировке, указав соответствующие значения 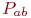и .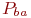

Последняя модель таких возможностей не имеет.

увеличить изображение
Рис. 3.27. Блок-схема модели "блуждание частицы по решетке"

Date: 2015-07-17; view: 429; Нарушение авторских прав