
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет теоретических частот по распределению типа В
|
|
При этом типе распределения абсолютное значение асимметрии превышает 0,75-0,80, при критерии достоверности более 2.
Теоретические частоты при распределении типа В рассчитываются по формуле:
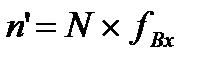
В этой формуле используется численность вариационного ряда и функция распределения типа В:
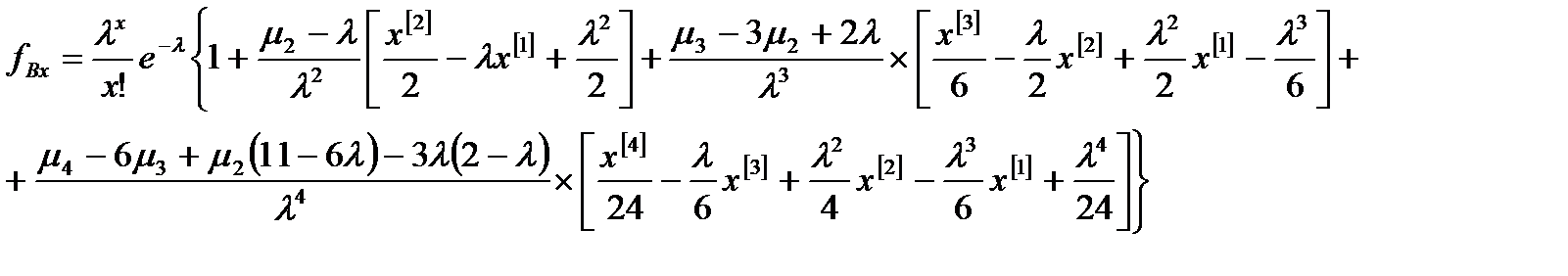
В этой формуле использованы значения центральных моментов (m) и первый начальный момент относительно нулевого значения (l). Функция распределения типа В весьма сложна и ее расчет целесообразно производить с применением компьютера и электронных таблиц. В этом случае необходимо рассчитать таблицу
Таблица 9
Расчет частот теоретического распределения по типу В
| x | x’ | n | S1 | λ | Pm | 0,537743 | +0,200643 ´ x[1] | -0,02096 ´ x[2] | -8,54373 ´10-5 ´ x[3] | -2,05585 ´10-5 ´ x[4] | = Σ | fB(X) =Pm(Σ) | nI=N*fB(X) |
| 8,25 | ---- | 4,4863 | 0,011262 | 0,537743 | 0,53774 | 0,00605 | 0,8842 | ||||||
| 9,95 | 0,050526 | 0,537743 | 0,20064 | 0,73839 | 0,03730 | 5,4469 | |||||||
| 11,65 | 0,113337 | 0,537743 | 0,40129 | -0,04192 | 0,89711 | 0,10167 | 14,8446 | ||||||
| 13,35 | 0,169488 | 0,537743 | 0,60193 | -0,12576 | -0,00051 | 1,01340 | 0,17176 | 25,0769 | |||||
| 15,05 | 0,190093 | 0,537743 | 0,80257 | -0,25151 | -0,00205 | -0,00049 | 1,08626 | 0,20649 | 30,1476 | ||||
| 16,75 | 0,170563 | 0,537743 | 1,00321 | -0,41918 | -0,00513 | -0,00247 | 1,11418 | 0,19004 | 27,7455 | ||||
| 18,45 | 0,127533 | 0,537743 | 1,20386 | -0,62878 | -0,01025 | -0,00740 | 1,09517 | 0,13967 | 20,3918 | ||||
| 20,15 | 0,081736 | 0,537743 | 1,40450 | -0,88029 | -0,01794 | -0,01727 | 1,02674 | 0,08392 | 12,2526 | ||||
| 21,85 | 0,045836 | 0,537743 | 1,60514 | -1,17372 | -0,02871 | -0,03454 | 0,90592 | 0,04152 | 6,0625 | ||||
| 23,55 | 0,022848 | 0,537743 | 1,80579 | -1,50906 | -0,0431 | -0,06217 | 0,72924 | 0,01666 | 2,4326 | ||||
| 25,25 | 0,01025 | 0,537743 | 2,00643 | -1,88633 | -0,06151 | -0,10361 | 0,49271 | 0,00505 | 0,7374 | ||||
| 146,0226 |
В этой таблице значения получены:
x’ – условные значения классов. Принимаются равным 0 для наименьшего класса с последующим увеличением.
S1 - последовательная сумма частот, начиная с наибольшего (последнего) класса;
λ – начальный момент относительно нулевого значения:
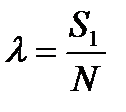
Pm – фрагмент функции распределения В:
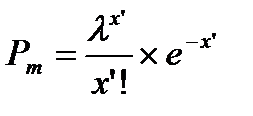
коэффициенты для колонок 7-11 получены по следующим формулам:
для колонки 7:
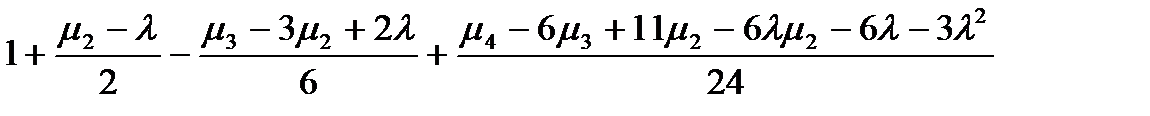
для колонки 8:
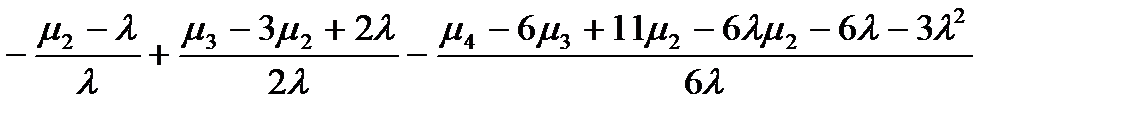
для колонки 9:
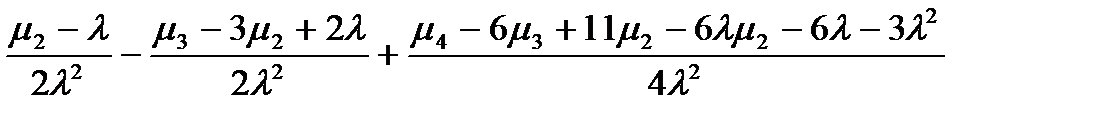
для колонки 10:
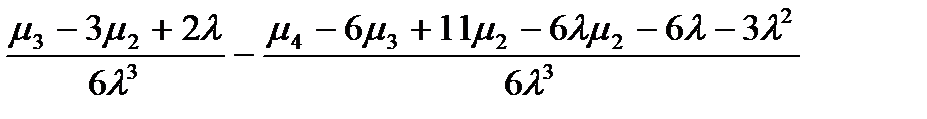
для колонки 11:
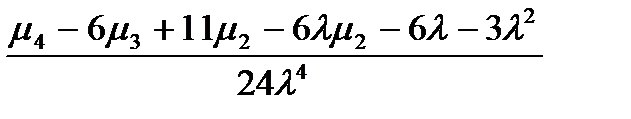
Значения x[1] - x[4] вычислены по формулам:
x[1]=x’; x[2]=x’´(x’-1); x[3]=x’´(x’-1) ´(x’-2); x[4]=x’´(x’-1) ´(x’-2) ´(x’-3)
Колонка 12 представляет собой сумму по колонкам с 7 по 11. Дальнейшие расчеты пояснений не требуют.
Проверкой правильности выполнения расчетов служит сумма по колонке теоретических частот, которая приблизительно должна равняться численности вариационного ряда.
Для всех приведенных выше видов теоретического распределения можно утверждать, что правильность выполнения расчетов и совпадение теоретической и фактической численности вариационного ряда не является гарантией того, что данный тип распределения достоверно отражает фактические данные. Для проверки правильности выбора теоретического распределения необходимо рассчитать критерий согласия теоретических частот с фактическими – критерий Пирсона.
Date: 2015-07-17; view: 536; Нарушение авторских прав