
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа. Корреляция большой выборочной совокупности
|
|
Показатели корреляции большой выборочной совокупности рассчитываются с использованием группировки по классовым интервалам. Но группировка выполняется одновременно по двум показателям – в двухмерной таблице, вертикаль которой представляет собой классы по ряду у, а горизонталь – классы по ряду х.
Классы по ряду х у нас уже сформированы (см. группировка выборочной совокупности). Необходимо сформировать классы по ряду у. Делается это по тем же правилам, что и для ряда х: сначала определяется оптимальное количество и размер класса (количество классов может отличаться от ряда х), затем определяются границы и средние значения классов.
| Наибольшее | 0,0463 | +0,0001 | 0,0464 | ||
| Наименьшее | 0,0066 | -0,0002 | 0,0064 | ||
| Амплитуда | 0,0397 | ||||
| 0,00496 | 0,00441 | 0,00397 | |||
| ~ | 0,0050 | 0,0045 | 0,0040 | ||
| Искусственное расширение | |||||
| 0,0050 | 0,0003 | ||||
| 0,0045 | 0,0008 | ||||
| 0,0040 | 0,0003 |
На основании расчетов мы выделяем в ряде у 8 классов с размером класса 0,0050.
Группировка данных выполняется в виде таблицы распределения вариант. Строки в этой таблице соответствуют классам по ряду у, а столбцы – классам по ряду х. Каждое дерево (для которых измерены исследуемые показатели) проверяется на принадлежность к классам по каждому из показателей. На основании этого определяется строка и столбец, к которым относятся показатели дерева и на их пересечении ставится точка.
Таблица 12
Таблица распределения вариант
| от | 9,1 | 10,9 | 12,6 | 14,3 | 17,7 | 19,4 | 21,1 | 22,8 | ny | Spx | хфакт | |||
| до | 10,8 | 12,5 | 14,2 | 15,9 | 17,6 | 19,3 | 22,7 | 24,4 | ||||||
| от | до | х ср у ср | 9,95 | 11,65 | 13,35 | 15,05 | 16,75 | 18,45 | 20,15 | 21,85 | 23,55 | |||
| 0,0064 | 0,0114 | 0,0089 | 222,8 | 11,14 | ||||||||||
| 0,0115 | 0,0164 | 0,0139 | 400,5 | 13,35 | ||||||||||
| 0,0165 | 0,0214 | 0,0189 | 523,6 | 15,4 | ||||||||||
| 0,0215 | 0,0264 | 0,0239 | 430,65 | 17,226 | ||||||||||
| 0,0265 | 0,0314 | 0,0289 | 401,05 | 19,09762 | ||||||||||
| 0,0315 | 0,0364 | 0,0339 | 246,9 | 20,575 | ||||||||||
| 0,0365 | 0,0414 | 0,0389 | . 1 | 21,85 | 21,85 | |||||||||
| 0,0415 | 0,0464 | 0,0439 | 70,65 | 23,55 | ||||||||||
| nx | ||||||||||||||
| Spy | 0,0534 | 0,1802 | 0,3058 | 0,5659 | 0,5625 | 0,543 | 0,5363 | 0,1406 | 0,1317 | |||||
| уфакт | 0,0089 | 0,0100 | 0,0139 | 0,0182 | 0,0225 | 0,0271 | 0,0315 | 0,0351 | 0,0439 |
В качестве проверки правильности выполнения группировки можно использовать данные по частотам ряда х. Они должны точно соответствовать строке nx таблицы распределения. При обнаружении несоответствия нужно найти и исправить ошибку, которая содержится либо в таблице распределения, либо в таблице группировки данных по ряду х. В последнем случае необходимо выполнить перерасчет всех связанных с таблицей данных параметров.
Строка Spy и столбец Spx представляют собой последовательное суммирование по столбцам и по строкам соответственно произведений данных группировки на среднее значение класса.
уфакт и хфакт рассчитываются по формулам:
 ;
; 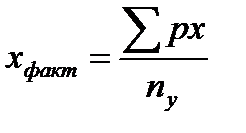
Для расчета характеристик связи большой выборочной совокупности необходимо построение корреляционной таблицы. В ней используются результаты группировки данных по двум показателям.
Для вычисления показателей рядов и взаимосвязи используются начальные отклонения а по ряду х и b по ряду у(методика расчета приведена в разделе «Вычисление начальных моментов по способу произведений»).
Строка na (столбец nb)представляет собой произведение частоты соответствующего класса на начальное отклонение по этому классу.
Строка Spb (столбец Spа) получен путем суммирования произведений частот, указанных в клетках таблицы на начальные отклонения, соответствующие этим клеткам.
Корреляционная таблица обладает несколькими проверочными суммами. Они показаны стрелками и должны совпадать.
Для расчета показателей мы должны получить начальные моменты.
Таблица 13
Корреляционная таблица
| xср | 9,95 | 11,65 | 13,35 | 15,05 | 16,75 | 18,45 | 20,15 | 21,85 | 23,55 | ny | nb | nb2 | Spa | bSpa | |
| уср | a b | -3 | -2 | -1 | |||||||||||
| 0,0089 | -2 | -40 | -46 | ||||||||||||
| 0,0139 | -1 | -30 | -30 | ||||||||||||
| 0,0189 | |||||||||||||||
| 0,0239 | |||||||||||||||
| 0,0289 | |||||||||||||||
| 0,0339 | |||||||||||||||
| 0,0389 | |||||||||||||||
| 0,0439 | |||||||||||||||
| nx | 52 | 71 | 462 | ||||||||||||
| na | -18 | -36 | -22 | 71 | |||||||||||
| na2 | |||||||||||||||
| Spb | -12 | -32 | -22 | -4 | 52 | ||||||||||
| aSpb | 462 | ||||||||||||||
| (Spb)2 | |||||||||||||||
| (Spb)2/nx | 24,000 | 56,888 | 22,000 | 0,516 | 12,960 | 54,450 | 108,764 | 42,250 | 75,000 | 396,829 |
Date: 2015-07-17; view: 462; Нарушение авторских прав