Определение констант ортотропии элементов при плоском напряженном состоянии

3.1.1. Результаты экспериментальных исследований строительных конструкций или их моделей, как правило, включают данные испытаний образцов материала в виде кубов и призм из бетона (ГОСТ 24452-80) и арматуры (ГОСТ 12004-81), такие как R_пр, R, E (бетон) и σ_т, σ_п (арматура).

Для расчета конструкций в упругой стадии работы или оценки их несущей способности методом предельного равновесия возможно ограничиться имеющимися характеристиками материалов, полученными экспериментально или принятыми по данным нормативов.

3.1.2. Для расчетного моделирования поведения конструкций за пределами упругости рекомендуется использовать методики, вкоторых текущая характеристика жесткости материала определяется как функция ее начального значения и некоторых параметров нелинейности [31]. При этом для описания характеристик железобетона как композитного материала могут быть использованы усредненные данные как для однородного ортотропного материала [32], так и для материала, состоящего из бетона и арматуры с учетом их взаимодействия [33]. При моделировании конструкции, элементы которой работают в плоском напряженном состоянии, может быть использована методика, основанная на экспериментальном определении констант ортотропии железобетона как однородного материала [16, 34 - 36], исходя из следующих гипотез;

композитный материал - железобетон - может быть заменен ортотропным, деформативные характеристики которого позволяют установить интегральную зависимость между напряжениями и деформациями в пределах некоторой малой области железобетонного образца;

в пределах этой малой области константы ортотропии постоянны и зависят от соотношения средних значений напряжений по области;

константы ортотропии соответствуют мгновенно-упругому состоянию материала и подчиняются принципу квантования, принимая дискретные значения, соответствующие соотношению главных напряжений, и изменяются скачкообразно при достижении соотношения напряжений граничных значений, определяющих параметрические состояния материала;

по границам между областями выполняются условия совместности деформаций.

В качестве основы для численного решения задачи о напряженно-деформированном состоянии конструкции принимается расчетная модель МКЭ. С учетом этого в качестве области, на которую распространяются указанные гипотезы, может быть каждый КЭ.

В соответствии с этими гипотезами можно считать, что изменение констант жесткости связано с некоторыми характерными состояниями материала, зависящими от уровня и соотношения напряжений (рис. 11).

Так как в общем случае в плоском напряженном состоянии возможны воздействия в виде сдвигающих усилий, области состояний представляют собой некоторую выпуклую поверхность (согласно постулату Д. Друккера - Р. Хилда). Тогда графики рис. 11 можно рассматривать как линии пересечения этой поверхности с плоскостями σ_x - σ_y. Для получения таких кривых параметрических состояний железобетонного элемента можно использовать данные эксперимента. Полученные физические константы материала оказываются однозначно связанными с соотношением величины напряжений.

3.1.3. Для расчета конструкции, элементы которой находятся в плоском напряженном состоянии, необходимо знание таких характеристик материала: E₁; E₂; μ₁₂; μ₂₁; G₁₂. С учетом известного соотношения:

четыре параметра из пяти независимы и могут быть определены экспериментально из уравнений закона Гука для двухосного напряженного состояния:

.

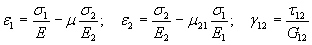(40)

3.1.4. В общем случае для определения констант по п. 3.1.3 необходимо провести испытание плоского образца железобетонной конструкции при четырех независимых напряженных состояниях. Используя возможность создания одноосного напряженного состояния, получим разделяющую систему из двух уравнений, из решения которых найдем соответственно неизвестные для одного из направлений:

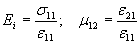
	(41)
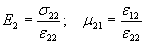
	(42)

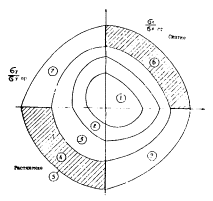
Рис. 11. Качественный график параметрических областей плоского напряженного состояния

1 - зона упруго-линейных деформаций; 2 - зона микротрещин; 3 - зона макротрещин; 4 - зона текучести арматуры; 5 - граница прочности; 6 -зона пластичности; 7 - зона прогрессирующего разрушения

Так как реализация сдвиговой нагрузки в эксперименте на образце затруднена, получаем касательные напряжения под углом 45° к осям ортотропии, создавая нагрузку разных знаков по двум перпендикулярным направлениям (рис. 12).

3.1.5. Согласно пп 3.1.3 и 3.1.4 могут быть экспериментально определены константы для области упругого поведения материала. Поскольку процессу деформирования свойственна нелинейность, экспериментальное определение констант жесткости возможно только для приращений напряжений или деформаций, в соответствии с методом "малых параметров" или "упругих решений" в задачах расчета нелинейно-деформируемого тела при следующем порядке нагружения образцов:

согласно принятому варианту в плоском напряженном состоянии повышается уровень напряжений до определенной точки на графике σ_x - σ_y;

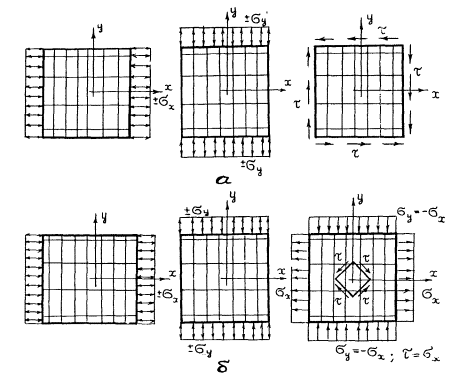
Рис. 12. Напряженные состояния для определения констант ортотропии плоского напряженного состояния

а - теоретические напряженные состояния; б - напряженные состояния, реализуемые в эксперименте

нагрузке дается приращение, достаточно малое по величине, чтобы изменить состояние материала (производятся микронагpyжения, при которых замеряются приращения деформаций и выполняются необходимые вычисления для определения констант ортотропии по зависимостям (40), (41), (42).

3.1.6. Для реализации видов напряженного состояния по п. 3.1.5 рекомендуется специальная установка, позволяющая осуществлять с помощью восьми призм нагружение железобетонного образца при двустороннем сжатии или растяжении сжатии по одной и растяжении по другой оси. Равномерность воздействия обеспечивается устройством распределительной системы, представляющей собой четыре ряда статически определимых балок на двух опорах в соотношении по рядам 8:4:2:1. Передача растягивающих напряжений на образец осуществляется через выпуски арматуры посредством системы тяжей с выходом на домкрат. Соотношение количества тяжей, считая выпуски арматуры, в последовательных группах 8:4:2:1.

Конструктивно установка (монтируется в силовой замкнутой раме) может быть в трех вариантах: УРО - устройство растяжения образцов; УСО - устройство сжатия образцов; УРСО - устройство растяжения-сжатия образцов.

3.1.7. В.соответствии с устройством, принципом действия и назначением установки может быть определен вид образцов материала. Образцы по форме представляют собой квадратные пластины размером 6,4×0,4×0,07 м, имеющие гладкую лицевую и торцовую поверхность. В случае необходимости по двум (четырем) противолежащим торцовым поверхностям имеются выпуски арматуры.

Вид армирования назначается из условий геометрического подобия натурной конструкции и образца заданных размеров. Для передачи растягивающих усилий к каждой паре выпусков арматуры привариваются скобы, которые служат захватами для нагрузочного устройства. В целях получения статистически достоверных результатов в каждой серии должно быть испытано не менее трех образцов, результаты испытаний должны быть обработаны в соответствии с требованиями ГОСТ 24452-80.

3.1.8. По результатам испытаний устанавливаются границы областей, в пределах которых параметры жесткости сохраняют постоянное значение при изменении величины соотношения напряжений.

Для описания границ этих областей могут быть использованы аналитические выражения, аппроксимирующие экспериментальные кривые в осях (± σ_x; ± σ_y).

Каждой области на графике напряжений соответствует набор из характеристик E₁; E₂; μ₁₂; μ₂₁; G, которые могут быть использованы как исходная информация к программе расчета конструкций, элементы которой работают в условиях плоского напряженного состояния. Для выполнения таких расчетов необходимо наличие в программной библиотеке КЭ расчетных модулей, позволяющих рассчитывать ортотропные КЭ. В наиболее распространенных программах (ЛИРА, ПРОКРУСТ) имеются такие типы КЭ.

Date: 2015-07-17; view: 1334; Нарушение авторских прав