
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение неизвестных параметров расчетных моделей
|
|
1.5.1. Для использования расчетных моделей при проведении численных исследований объекта необходимо, чтобы все параметры расчетной модели* были известны. Часть ее параметров (множество М = { mτ }) известна до начала исследований (например, геометрические размеры, граничные условия и т.д.), некоторые же (множество Χ = { xi }) не известны** и не могут быть достоверно вычислены только теоретически. Для их определения проводится специальный физический эксперимент.
* Расчетная модель считается заданной, если имеются в наличии расчетная схема и алгоритм, а при использовании ЭВМ - также программный комплекс, численно реализующий применяемый теоретический метод.
** Как правило, неизвестными параметрами расчетных моделей являются физико-механические характеристики элементов исследуемого объекта (например, жесткости отдельных участков конструкции, податливости узлов и т.д.), реже - геометрические характеристики некоторых расчетных элементов, аппроксимирующих в расчетной схеме реальный конструктивный элемент
1.5.2. Определение неизвестных параметров расчетных моделей по п. 1.5.1. с использованием результатов экспериментов выполняется двумя методами - прямым (неизвестный параметр получают непосредственно во время физического эксперимента измерением соответствующими приборами) и косвенным (неизвестные характеристики вычисляются как некоторые функции параметров, достоверно определенных в эксперименте).
1.5.3. Для дальнейшего корректного использования в расчетных моделях найденных по п. 1.5.2 параметров необходимо учитывать вероятностный характер результатов эксперимента.
1.5.4. При прямом методе определения неизвестных параметров сначала производится предварительная статистическая обработка полученных результатов, предполагающая исключение систематических погрешностей и резко выделяющихся значений (грубые ошибки измерений), затем - точечная и доверительная оценка параметра по формулам (2).
1.5.5. При косвенном методе определения неизвестных параметров возможны два случая:
неизвестный параметр - известная аналитическая функция других параметров, достоверно определяемых из эксперимента;
функциональная зависимость между неизвестными параметрами, полученными в эксперименте, не может быть представлена в виде аналитической функции.
В первом случае при:
| xi = fi (mr), | (7) |
(i = 1, 2, …., n; r = 1, 2, …, s)
точечная оценка неизвестного параметра:
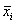 = fi (mr), = fi (mr),
| (8) |
где 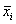 - точечные оценки неизвестных параметров;
- точечные оценки неизвестных параметров; 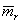 - точечные оценки параметров, получаемых непосредственно в результате прямых измерений, которые находим по формуле, аналогичной (2).
- точечные оценки параметров, получаемых непосредственно в результате прямых измерений, которые находим по формуле, аналогичной (2).
Доверительная оценка при заданной доверительной вероятности:
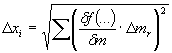 , ,
| (9) |
где Δmr - доверительные интервалы параметров, получаемых непосредственно из эксперимента, которые определяем по формуле, аналогичной (2).
1.5.6. При решении задачи определения параметров расчетной модели во II случае имеем обратную функциональную зависимость:
| yj = φj (m1, m2, …, mr, x1, x2, …, xn), | (10) |
(j = 1, 2, …, m)
где yj - некоторый параметр напряженно-деформированного состояния конструкции, измеряемый экспериментально.
1.5.7. Как правило, количество измеряемых по п. 1.5.6 параметров должно быть больше или равно количеству неизвестных:
m > n. В этом случае задача определения неизвестных параметров расчетной модели включает:
аппроксимацию функции (10) полиномами сравнительно невысоких степеней;
приведение полученной системы m - нелинейных уравнений к избыточной m - l - линейных, причем m - l ≥ n;
определение точечных и доверительных оценок xi подстановкой в уравнение экспериментальных значений уэi - и приведением избыточной системы линейных уравнений к системе нормальных уравнений метода наименьших квадратов [21].
1.5.8. Аппроксимация функций (10) полиномами по п. 1.5.7 проводится с применением математической теории планирования экспериментов [23, 24], для чего при помощи выбранной расчетной модели объекта выполняется серия численных экспериментов-расчетов, в которых искомые неизвестные параметры расчетной модели варьируются на нескольких уровнях, назначаемых априори из опыта и по интуиции исследователя.
1.5.9. В случае, когда заранее известно, что между показателем напряженно-деформированного состояния yj и неизвестными параметрами расчетной модели существует линейная зависимость, проведение численного эксперимента осуществляется по матрицам планирования (см. приложение 1), а функция (10) аппроксимируется полиномом первой степени:
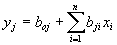 , ,
| (11) |
(i = 1, 2,… n; j = 1, 2, …, m)
где
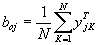 ; ;
| (12) |
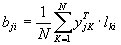
N - число расчетов - строк матрицы планирования;  - расчетное значение, параметра yj в К -том расчете; lki - элемент матрицы планирования на пересечении К -той строки и i -того столбца.
- расчетное значение, параметра yj в К -том расчете; lki - элемент матрицы планирования на пересечении К -той строки и i -того столбца.
Примечания: 1. При этом неизвестные параметры расчетной модели варьируются в двух уровнях: (+1) - в верхнем и (-1) - в нижнем.
2. В зависимости от количества неизвестных параметров матрицу планирования выбираем, принимая наименьшую матрицу, число строк которой N > п, а количество столбцов равным n (лишние столбцы выбранной матрицы вычеркиваются).
1.5.10. В случае, когда устанавливается наличие линейной зависимости между yj, и xi, с точностью, достаточной для решения практических задач, функцию (10) достаточно аппроксимировать полиномом второй степени:
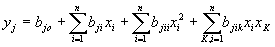 ; ;
| (13) |
(i = 1, 2, …, n; j = 1, 2, …, m; K = 1, 2, …, n; K ≠ i)
с варьированием неизвестных параметров расчетной модели трех уровнях:
верхнем (+1);
среднем (0);
нижнем (-1)*.
Примечание. Матрицы планирования второго порядка и формулы для вычисления коэффициентов уравнений (13) см. в приложении 1.
* Значения неизвестных параметров расчетной модели, соответствующие среднему значению, называются также центром плана и обозначаются xoi. Натуральные значения верхнего и нижнего уровня рассматриваемого параметра определяется по формулам ximax = Χoi + Р и ximin = Χoi - P, где P - интервал варьирования параметра хi.
1.5.11. Система нелинейных уравнений (13) может быть приведена к системе линейных, для чего количество параметров 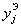 , намеченных для измерения в физическом эксперименте, должно быть больше количества неизвестных параметров расчетной модели, как минимум, на число нелинейных членов. После несложных алгебраических преобразований нелинейные члены могут быть исключены, тогда общее число уравнений в системе (13) будет т - l, где l - число нелинейных членов. Более эффективен метод обеспечения адекватности линейных уравнений (11), выражающийся в переходе на новую систему неизвестных параметров расчетной модели. На основании теории подобия и размерностей можно записать безразмерные комплексы - критерии подобия исследуемого объекта, включающие известные и неизвестные параметры расчетной модели, причем количество используемых критериев подобия должно быть равно числу неизвестных параметров (к = 1, 2,.., n).
, намеченных для измерения в физическом эксперименте, должно быть больше количества неизвестных параметров расчетной модели, как минимум, на число нелинейных членов. После несложных алгебраических преобразований нелинейные члены могут быть исключены, тогда общее число уравнений в системе (13) будет т - l, где l - число нелинейных членов. Более эффективен метод обеспечения адекватности линейных уравнений (11), выражающийся в переходе на новую систему неизвестных параметров расчетной модели. На основании теории подобия и размерностей можно записать безразмерные комплексы - критерии подобия исследуемого объекта, включающие известные и неизвестные параметры расчетной модели, причем количество используемых критериев подобия должно быть равно числу неизвестных параметров (к = 1, 2,.., n).
1.5.12. Уравнения (10) с учетом п. 1.5.11 запишем в следующем виде:
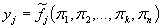 ; ;
| (14) |
где πk - критерий подобия.
При переходе к новым неизвестным параметрам расчетной модели:
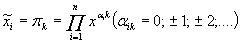 ; ;
| (15) |
параметры напряженно-деформированного состояния yi будут линейно зависеть от 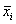 .
.
1.5.13. Система линейных уравнений относительно неизвестных параметров расчетной модели xi при подстановке в левые части уравнений (11) соответствующих экспериментальных значений параметров напряженно-деформированного состояния может быть записана в виде:
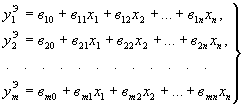
| (16) |
Примечание. Следует отметить, что если система (11) получена в результате преобразования из нелинейных уравнений, в левой части уравнений (16) будут линейные функции параметров напряженно-деформированного состояния.
Система (16) в матричном виде:
| Y = ВХ; | (17) |
где
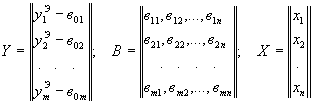
1.5.14. Для решения системы (16) как избыточной, т.е. с целью нахождения точечных и доверительных оценок xi, может быть использован метод наименьших квадратов [21] с приведением ее к полной системе нормальных уравнений:
| F = C Х; | (18) |
где
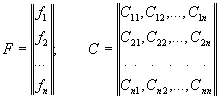
Преобразование системы (16) в (18) производится по формулам:
| F = BTY; C = BBT | (19) |
где ВT - транспонированная матрица В
1.5.15. Для удобства вычислений без применения ЭВМ запишем матрицы F и С в развернутом виде
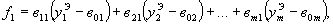
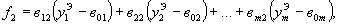
| (20) |
.........
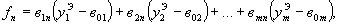
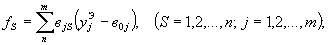

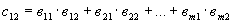
| (21) |
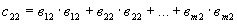
......
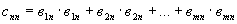

1.5.16. Точечные оценки неизвестных параметров расчетной модели 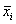 ,находятся из решения системы нормальных уравнений (18).
,находятся из решения системы нормальных уравнений (18).
1.5.17. Доверительными интервалами для 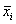 могут считаться границы [
могут считаться границы [ 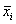 - Δxi,
- Δxi, 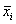 + Δxi ]:
+ Δxi ]:
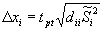
| (22) |
где. tpt - коэффициент Стьюдента, определяемый по таблицам t -распределения при заданной доверительной вероятности P и числе степеней свободы j = т - п; dii - соответствующий диагональный элемент матрицы D= С-1; Si - точечная оценка стандарта σi, определяемая из выражения:
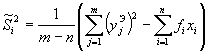
| (23) |
1.5.18. Из решения системы (18) получаем значения неизвестных параметров xi в нормированном виде, переход к абсолютным значениям осуществляется с учетом выражений (14) по формулам:
Χi = Χ 0i + pxi;
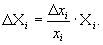
| (24) |
1.5.19. Если предварительные численные исследования с целью получения уравнений (11) проводятся после завершения эксперимента, то нелинейную зависимость между yi и xi можно нейтрализовать, осуществив следующий итерационный процесс:
задаемся первоначальными значениями неизвестных параметров Χ0i и их интервалами варьирования Pi;
проводим численный эксперимент с целью получения уравнения (11);
подставив в уравнение (11) экспериментальные значения параметров напряженно-деформированного состояния 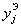 , по рекомендуемой методике находим первое приближение Χi и
, по рекомендуемой методике находим первое приближение Χi и 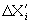 ;
;
приняв 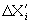 за новый центр плана, а | Χ0i -
за новый центр плана, а | Χ0i - 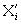 | за новый интервал варьирования, повторяем изложенный выше процесс;
| за новый интервал варьирования, повторяем изложенный выше процесс;
итерационный процесс заканчивается, когда интервал варьирования 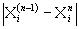 будет меньше доверительного
будет меньше доверительного 
Date: 2015-07-17; view: 1325; Нарушение авторских прав