
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Проблемы применения имитационного моделирования
|
|
Применение имитационного моделирования целесообразно при наличии определенного условия. Эти условия определил Р. Шеннон:
1. Не существует законченной математической постановки данной задачи, либо еще не разработаны аналитические методы решения сформулированной математической модели. К этой категории относятся многие модели массового обслуживания, связанные с рассмотрением очередей.
2. Аналитические методы имеются, но математические процедуры столь сложны и трудоемки, что имитационное моделирование дает более простой способ решения задачи.
3. Кроме оценки определенных параметров, желательно осуществить на имитационной модели наблюдение за ходом процесса в течение определенного периода.
Дополнительным преимуществом имитационного моделирования можно считать широчайшие возможности его применения в сфере образования и профессиональной подготовки. Разработка и использование имитационной модели позволяет экспериментатору видеть и "разыгрывать" на модели реальные процессы и ситуации.
Необходимо обозначить ряд проблем, возникающих в процессе моделирования систем. Исследователь должен акцентировать на них внимание и попытаться их разрешить, дабы избежать получения недостоверных сведений об изучаемой системе.
Первая проблема, которая касается и аналитических методов моделирования, состоит в нахождении "золотой середины" между упрощением и сложностью системы. По мнению Шеннона искусство моделирования в основном состоит в умении находить и отбрасывать факторы, не влияющие или незначительно влияющие на исследуемые характеристики системы. Нахождение этого "компромисса" во многом зависит от опыта, квалификации и интуиции исследователя. Если модель слишком упрощена и в ней не учтены некоторые существенные факторы, то высока вероятность получить по этой модели ошибочные данные, с другой стороны, если модель сложная и в нее включены факторы, имеющие незначительное влияние на изучаемую систему, то резко повышаются затраты на создание такой модели и возрастает риск ошибки в логической структуре модели. Поэтому перед созданием модели необходимо проделать большой объем работы по анализу структуры системы и взаимосвязей между ее элементами, изучению совокупности входных воздействий, тщательной обработке имеющихся статистических данных об исследуемой системе.
Вторая проблема заключается в искусственном воспроизводстве случайных воздействий окружающей среды. Этот вопрос очень важен, так как большинство динамических производственных систем являются стохастическими, и при их моделировании необходимо качественное несмещенное воспроизведение случайности, в противном случае, результаты, полученные на модели, могут быть смещенными и не соответствовать действительности. Существует два основных направления разрешения этой проблемы: аппаратная и программная (псевдослучайная) генерация случайных последовательностей. При аппаратном способе генерации случайные числа вырабатываются специальным устройством. В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т.д. Недостатками аппаратного способа получения случайных чисел является отсутствие возможности проверки (а значит гарантии) качества последовательности во время моделирования, а также невозможности получения одинаковых последовательностей случайных чисел. Программный способ основан на формировании случайных чисел с помощью специальных алгоритмов. Этот способ наиболее распространен, так как не требует специальных устройств и дает возможность многократного воспроизведения одинаковых последовательностей. Его недостатками являются погрешность в моделировании распределений случайных чисел, вносимую по причине того, что ЭВМ оперирует с n-разрядными числами (т.е. дискретными), и периодичность последовательностей, возникающую в силу их алгоритмического получения. Таким образом, необходима разработка методов улучшения и критериев проверки качества генераторов псевдослучайных последовательностей.
Третьей наиболее сложной проблемой является оценка качество модели и полученных с ее помощью результатов (этап проблема актуальна и для аналитических методов). Адекватность моделей может быть оценена методом экспертных оценок, сравнением с другими моделями (уже подтвердившими свою достоверность), по полученным результатам. В свою очередь, для проверки полученных результатов часть из них сравнивается с уже имеющимися данными.
Математические модели систем
Важным этапом моделирования является создание математической модели исследуемой системы. На базе математической модели происходит анализ характеристик системы, при компьютерном моделирования на основе математической модели создается алгоритм программ для получения информации о поведении системы. Формальное описание объекта исследование необходимо также для взаимопонимания между специалистами разных областей, объединенных для решения какой-либо глобальной задачи.
В общем случае математическую модель любой динамической системы можно представить в следующем виде:
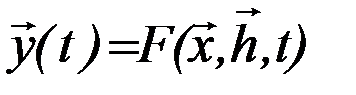 ,
,
где 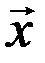 - совокупность входных воздействий на систему,
- совокупность входных воздействий на систему,
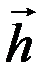 - совокупность внутренних параметров системы,
- совокупность внутренних параметров системы,
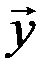 - совокупность выходных характеристик системы,
- совокупность выходных характеристик системы,
F - закон функционирования системы.
Процесс функционирования системы можно рассматривать как последовательную смену состояний 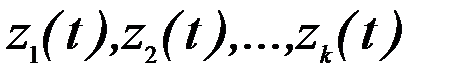 :
:
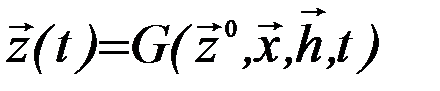 ,
,
где 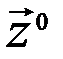 - совокупность начальных состояний.
- совокупность начальных состояний.
Таким образом, общую математическую модель системы можно также представить следующим образом:
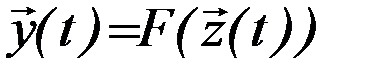 .
.
При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный, дискретно-детерминированный, дискретно-стохастический, непрерывно-стохастический, сетевой, обобщенный (или универсальный). Соответственно этим подходам были разработаны типовые математические схемы создания моделей.
1. Непрерывно-детерминированный подход использует в качестве математических моделей системы дифференциальных уравнений (см. выше).
Простейшую систему автоматического управления можно представить в следующем виде:
| Управляющай система |
| Объект управления |
Разность между заданными yзад(t) и действительным y(t) законами изменения управляемой величины есть ошибка управления h'(t)=yзад(t)-y(t). Если предписанный закон изменния управляемой величины соответствует закону изменения входного (задающего) воздействия, т.е. x(t)=y(t), то h'(t)=x(t)-y(t).Принцип обратной связи (основной принцип систем автоматического управления): приведение в соответствие выходной переменной y(t) ее заданному значению используется информация об отклонении h'(t) между ними. Задачей системы автоматического управления является изменение выходных сигналов согласно заданному закону с определенной точностью (с допустимой ошибкой).
2. Дискретно-детерминированный подход реализуется с помощью математического аппарата теории автоматов. Система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Математической моделью при этом подходе является конечный автомат, характеризующийся конечным множеством X входных сигналов, конечным множеством Y выходных сигналов, конечным множеством Z внутренних состояний, начальным состоянием Z0 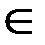 Z; функцией переходов g(z,x); функцией выходов v(z,x). Автомат функционирует в дискретном автоматном времени, моментами которого являются такты (примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния).
Z; функцией переходов g(z,x); функцией выходов v(z,x). Автомат функционирует в дискретном автоматном времени, моментами которого являются такты (примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния).
Работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t+1) и выдачей некоторого выходного сигнала. Например, автомат первого рода (автомат Мили) описывается следующим образом:
z(t+1)=g[z(t),x(t)], t=0,1,2,...;
y(t)=v[z(t),x(t)], t=0,1,2,...;
для автомата второго рода:
z(t+1)=g[z(t),x(t)], t=0,1,2,...;
y(t)=v[z(t),x(t-1)], t=1,2,3...;
Автомат, для которого функция выходов не зависит от входной переменной x(t), называется автоматом Мура:
y(t)=v[z(t)], t=0,1,2,...
Различают автоматы с памятью (имеют более одного состояния) и автоматы без памяти (обладают одним состоянием), синхронные ("считывает" входные сигналы в моменты времени, которые определяются синхронизирующими сигналами) и асинхронные (считывают входной сигнал непрерывно) автоматы.
Существует несколько способов задания работы F-автоматов, но наиболее часто используются табличный, графический и матричный.
Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы - его состояниям. При этом обычно первый слева столбец соответствует начальному состоянию z0. На пересечении i-й строки и k-го столбца таблицы переходов помещается соответствующее значение g (zk, xi) функции переходов, а в таблице выходов - соответствующее значение v (zk, xi) функции выходов. Для конечного автомата Мура обе таблицы можно совместить, получив так называемую отмеченную таблицу переходов, в которой над каждым состоянием zk автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию, согласно, выходной сигнал v (zi).
Описание работы конечного автомата Мили таблицами переходов g и выходов v иллюстрируется табл. 1., а описание конечного автомата Мура - таблицей переходов (табл. 2).
Таблица 1
| xi | zk | |||
| z0 | z1 | ... | zk | |
| Переходы | ||||
| x1 | g(z0,x1) | g(z1,x1) | ... | g(zk,x1) |
| x2 | g(z0,x2) | g(z1,x2) | ... | g(zk,x2) |
| ... | ... | ... | ... | ... |
| xk | g(z0,xk) | g(z1,xk) | ... | g(zk,xk) |
| Выходы | ||||
| x1 | v(z0,x1) | v(z1,x1) | ... | v(zk,x1) |
| x2 | v(z0,x2) | v(z1,x2) | ... | v(zk,x2) |
| ... | ... | ... | ... | ... |
| xk | v(z0,xk) | v(z1,xk) | ... | v(zk,xk) |
Таблица 2
| xi | v(zk) | |||
| v(z0) | v(z1) | ... | v(zk) | |
| z0 | z1 | ... | zk | |
| Переходы | ||||
| x1 | g(z0,x1) | g(z1,x1) | ... | g(zk,x1) |
| x2 | g(z0,x2) | g(z1,x2) | ... | g(zk,x2) |
| ... | ... | ... | ... | ... |
| xk | g(z0,xk) | g(z1,xk) | ... | g(zk,xk) |
Примеры табличного способа задания конечного автомата Мили приведены в табл. 3, а для автомата Мура в табл. 4.
Таблица 1
| xi | zk | ||
| z0 | z1 | z2 | |
| Переходы | |||
| x1 | z2 | z0 | z0 |
| x2 | z0 | z2 | z1 |
| Выходы | |||
| x1 | y1 | y1 | y2 |
| x2 | y1 | y2 | y1 |
Таблица 2
| xi | y | ||||
| y1 | y1 | y3 | y2 | Y3 | |
| z0 | z1 | z2 | z3 | Z4 | |
| x1 | z1 | z4 | z4 | z2 | Z2 |
| x2 | z3 | z1 | z1 | z0 | Z0 |
При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершин дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал xk вызывает переход из состояния zi в состояние zj, то на графе автомата дуга, соединяющая вершину zi с вершиной zj обозначается xk. Для того, чтобы задать функцию переходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производиться так: если входной сигнал xk действует на состояние zi, то согласно сказанному получается дуга, исходящая из zi и помеченная xk; эту дугу дополнительно отмечают выходным сигналом y=y(zi, xk). Для автомата Мура аналогичная разметка графа такова: если входной сигнал xk, действуя на некоторое состояние автомата, вызывает переход в состояние zj, то дугу, направленную в zj и помеченную xk, дополнительно отмечают выходным сигналом y=y(zj, xk). На рис. 1 приведены заданные ранее таблицами F- автоматы Мили F1 и Мура F2 соответственно.

Рис. 1. Графы автоматов Мили (а) и Мура (б).
При решении задач моделирования часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С=|| cij ||, строки которой соответствуют исходным состояниям, а столбцы - состояниям перехода. Элемент cij=xk/yS в случае автомата Мили соответствует входному сигналу xk, вызывающему переход из состояния zi в состояние zj и выходному сигналу yS, выдаваемому при этом переходе. Для автомата Мили F1, рассмотренного выше, матрица соединений имеет вид:
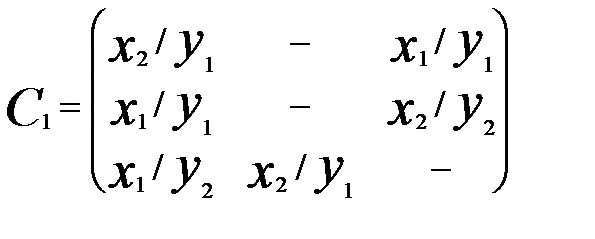
Если переход из состояния zi в состояние zj происходит под действием нескольких сигналов, элемент матрицы cij представляет собой множество пар "вход/выход" для этого перехода, соединённых знаком дизъюнкции.
Для F- автомата Мура элемент cij равен множеству входных сигналов на переходе (zizj), а выход описывается вектором выходов:
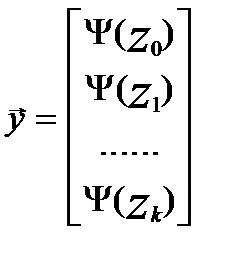 i-ая компонента которого выходной сигнал, отмечающий состояние zi
i-ая компонента которого выходной сигнал, отмечающий состояние zi
Пример. Для рассмотренного ранее автомата Мура F2 запишем матрицу состояний и вектор выходов:
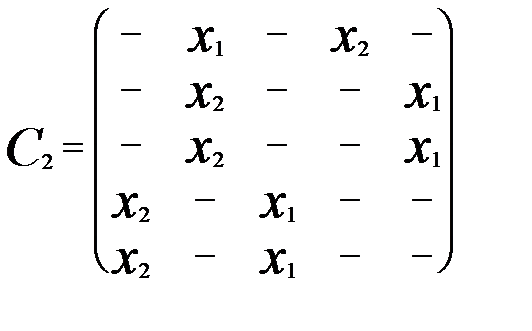 ;
; 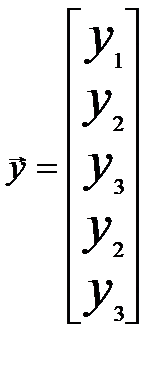
Для детерминированных автоматов переходы однозначны. Применительно к графическому способу задания F- автомата это означает, что в графе F- автомата из любой вершины не могут выходить 2 и более ребра, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза.
Рассмотрим вид таблицы переходов и графа асинхронного конечного автомата. Для F- автомата состояние zk называется устойчивым, если для любого входа xiÎX, для которого j(zk,xi)=zk имеет место y(zkxi)=yk. Т.о. F- автомат называется асинхронным, если каждое его состояние zkÎZ устойчиво.
На практике всегда автоматы являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например, введением сигналов синхронизации. На уровне абстрактной теории удобно часто оперировать с синхронными конечными автоматами.
Пример. Рассмотрим асинхронный F- автомат Мура, который описан в табл. 5 и приведён на рис. 2.
Таблица 5
| y | |||
| xi | y1 | y2 | y3 |
| z0 | z1 | z2 | |
| x1 | z1 | z1 | z1 |
| x2 | z2 | z1 | z2 |
| x3 | z0 | z0 | z2 |

Рис. 2.Граф асинхронного автомата Мура.
Если в таблице переходов асинхронного автомата некоторое состояние zk стоит на пересечении строки xS и столбца zS(S¹k), то это состояние zk обязательно должно встретиться в этой же строке в столбце zk.
С помощью F-схем описываются узлы и элементы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией (например, телефонные станции). Широта применения F-схем не означает их универсальность. Этот подход непригоден для описания процессов принятия решений, процессов в динамических системах с наличием переходных процессов и стохастических элементов.
3. Дискретно-стохастический подход использует в качестве математического аппарата вероятностные автоматы, которые можно определить как дискретные потактные преобразователи информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Для такого автомата характерно задание таблицы вероятностей перехода автомата в некоторое состояние и появления некоторого выходного сигнала в зависимости от текущего состояния и входного сигнала.
Исследование автомата может проводиться как аналитическими, так и имитационными (например, методом статистического моделирования) методами. Этот подход применим для изучения эксплуатационных характеристик производственных объектов (например, надежности, ремонтопригодности, отказоустойчивости и т.п.).
4. Непрерывно-стохастический подход применяется для формализации процессов обслуживания. Этот подход наиболее известен ввиду того, что большинство производственных (и не только производственных - экономических, технических и т.д.) систем по своей сути являются системами массового обслуживания. Типовой математической схемой моделирования таких систем являются Q-схемы (англ. queuing system – система организации очереди). В обслуживании можно выделить две элементарные составляющие: ожидание обслуживания и собственно обслуживание, а в любой системе массового обслуживания можно выделить элементарный прибор. Соответственно в этом приборе выделяют накопитель (Н) заявок, ожидающих обслуживания, некоторой емкостью; канал обслуживания (К); потоки событий (последовательность событий, происходящих одно за другим в какие-то случайные моменты времени): поток заявок на обслуживание wi, характеризующийся моментами времени поступления и атрибутами (признаками) заявок (например, приоритетами), и поток обслуживания ui, характеризующийся моментами начала и окончания обслуживания заявок.
| Н |
| К |
yi
wi
П
Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуется только моментами поступления этих событий и задается последовательностью {tn }={0<= t1<= t2 ... <= tn <=...}, где tn - момент наступления n-го события (неотрицательное вещественное число).
Потоком неоднородных событий называется последовательность {tn,fn }, где fn - набор признаков события (приоритет, принадлежность к какому-либо источнику и т.д.)
Рассмотрим поток, в котором события разделены интервалами времени, которые являются случайными величинами. Пусть интервалы независимы между собой. Тогда поток событий называется потоком с ограниченным последействием.
Поток событий называется ординарным, если вероятность того, что на малый интервал времени 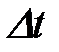 , примыкающий к моменту времени t, попадает больше одного события P>1(t,
, примыкающий к моменту времени t, попадает больше одного события P>1(t, 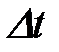 ) пренебрежительно мала по сравнению с вероятностью того, что на этот же интервал времени
) пренебрежительно мала по сравнению с вероятностью того, что на этот же интервал времени 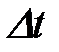 попадает ровно одно событие P1(t,
попадает ровно одно событие P1(t, 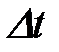 ). Для любого интервала
). Для любого интервала 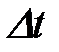 верно следующее:
верно следующее:
P0(t, 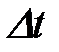 )+ P1(t,
)+ P1(t, 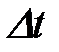 )+ P>1(t,
)+ P>1(t, 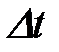 )=1
)=1
Как сумма вероятностей событий, образующих полную группу и несовместных. Тогда для ординарного потока событий справедливо следующее:
P0(t, 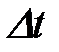 )+ P1(t,
)+ P1(t, 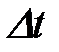 )=1, P>1(t,
)=1, P>1(t, 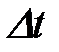 )=0(
)=0(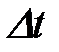 ).
).
Стационарным потоком событий называется поток, для которого вероятность появления того или иного числа событий на интервале времени зависит лишь от длины этого интервала и не зависит от того, где на оси времени взят этот интервал.
Рассмотрим на оси времени ординарный поток событий и найдем среднее число событий, наступающих на интервале времени 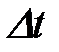 :
:
0·P0(t, 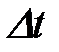 )+1·P1(t,
)+1·P1(t, 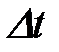 )= P1(t,
)= P1(t, 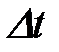 )
)
Тогда среднее число событий ординарного потока в единицу времени (интенсивность потока):
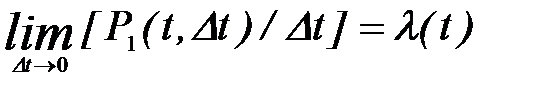
Для стационарного потока интенсивность постоянна.
Процесс функционирования прибора П можно представить как процесс изменения состояний его элементов во времени z(t). Переход в новое состояние для прибора означает изменение количества заявок, которые в нем находятся. Таким образом, вектор состояний для прибора имеет вид 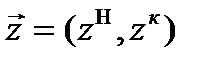 , где zн - состояние накопителя, zк - состояние канала.
, где zн - состояние накопителя, zк - состояние канала.
Если каналы различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальное Q-схема), а если приборы и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). В зависимости от емкости накопителя разделяют системы с потерями (емкость накопителя равна нулю), системы с ожиданием (емкость накопителя неограниченна) и системы смешанного типа (емкость накопителя ограничена).
Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения классов приоритетов. Различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы. Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций. Исходя из правил выбора заявок из накопителя на обслуживание каналом можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, ожидает окончания обслуживания предшествующей заявки каналом и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, прерывает обслуживание каналом заявки с более низким приоритетом и сама занимает канал.
При рассмотрении алгоритмов функционирования приборов обслуживания необходимо задать также набор правил, по которым заявки покидают накопители и каналы, например: блокировки по входу и выходу, маршрутизация заявок.
Аналитически модели систем массового обслуживания исследуются с помощью систем дифференциальных уравнений. Переменными в этих уравнениях являются вероятности переходов между состояниями (состояния, в свою очередь, определяются количеством и местонахождением заявок в системе).
Допустим процесс обслуживания начнется при отсутствии заявок в накопителе. Тогда состояния системы массового обслуживания описываются следующей системой уравнений:
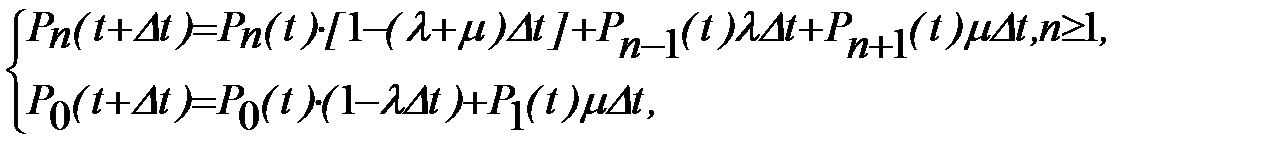
где 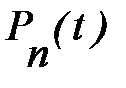 - вероятность нахождения системы в состоянии zn(t) Î Z в момент времени t, т.е. когда в ней имеется n заявок.
- вероятность нахождения системы в состоянии zn(t) Î Z в момент времени t, т.е. когда в ней имеется n заявок.
Эти уравнения следуют из того, что вероятность нахождения в системе n заявок в момент времени (t+Dt) равна вероятности нахождения в системе n заявок в момент t, умноженной на вероятность того, что за время Dt в систему не поступит ни одной заявки и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе (n-1) заявок в момент времени t, умноженная на вероятность того, что за время Dt поступит одна заявка и ни одна заявка обслужена не будет, плюс вероятность нахождения в системе (n+1) заявок в момент t, умноженная на вероятность того, что за время Dt одна заявак покинет систему и не поступит ни одной заявки. Вероятность того, что за время Dt не поступит ни одной заявки и ни одна заявка не покинет систему, равна 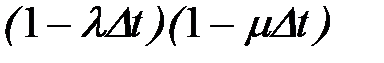 . Член, содержащий (Dt)2, при составлении дифференциального уравнения опускается. Следовательно, можно записать
. Член, содержащий (Dt)2, при составлении дифференциального уравнения опускается. Следовательно, можно записать 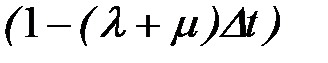 . Относительно остальных двух членов первого уравнения заметим, что
. Относительно остальных двух членов первого уравнения заметим, что
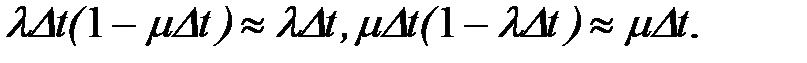
Перенеся 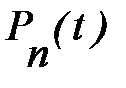 влево и устремив Dt к нулю, получим систему дифференциальных уравнений
влево и устремив Dt к нулю, получим систему дифференциальных уравнений
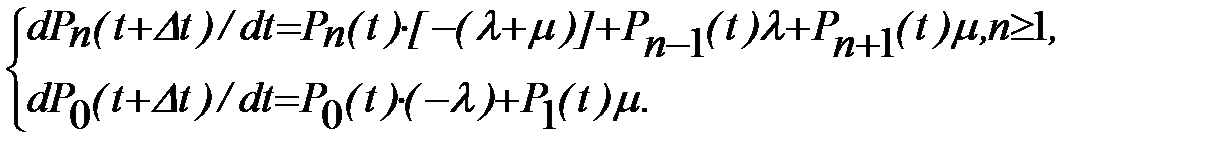
найдем выражение для математического ожидания числа заявок, находящихся в накопителе, и среднего времени ожидания заявок в накопителе для стационарного состояния r=l/m<1. Приравняв нулю производные по времени и исключив, таким образом, t из уравнений, получим систему алгебраических уравнений
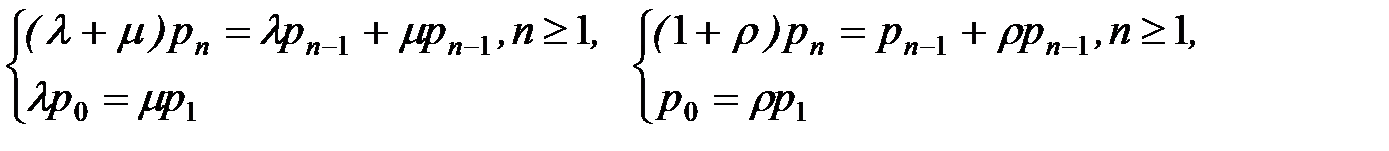
Пусть в первом уравнении n=1. Тогда (1+r)p1= p2+rp0 . Подставив сюда значение p1 из второго уравнения, находим p2=r2p0. Повторяя эти операции, получаем pn=rnp0 , причем 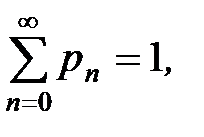 так как это сумма вероятностей того, что в системе нет ни одной заявки, имеется одна заявка, две заявки и т.д. Сумма этих вероятностей должна быть равна единице, так как рассматриваются все возможные состояния системы. Поэтому
так как это сумма вероятностей того, что в системе нет ни одной заявки, имеется одна заявка, две заявки и т.д. Сумма этих вероятностей должна быть равна единице, так как рассматриваются все возможные состояния системы. Поэтому 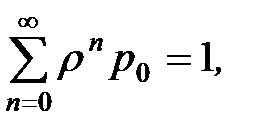
Или 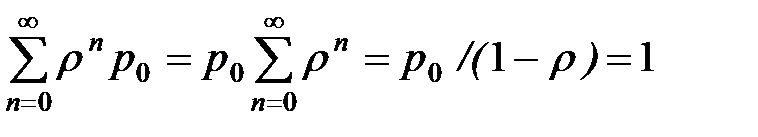 , откуда
, откуда 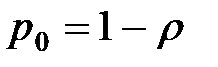 . Следовательно,
. Следовательно, 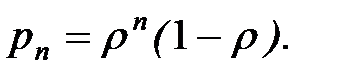
Математическое ожидание числа заявок, находящихся в системе (приборе),
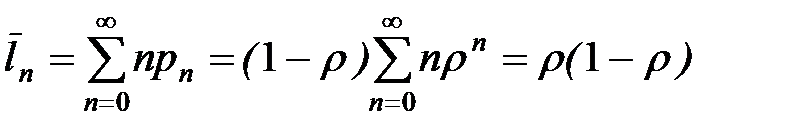 .
.
Колебания числа заявок, ожидающих обслуживания, что можно оценить с помощью дисперсии:
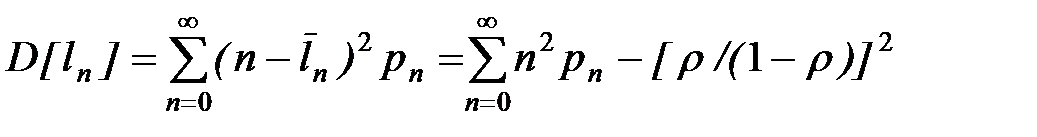 .
.
При этом
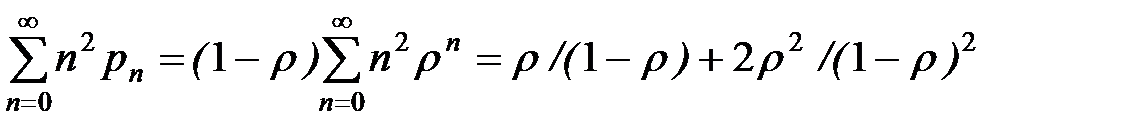 .
.
Следовательно,
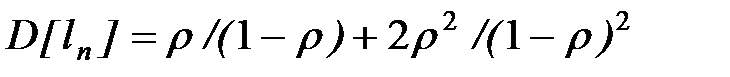 .
.
Математическое ожидание числа заявок, находящихся в накопителе,
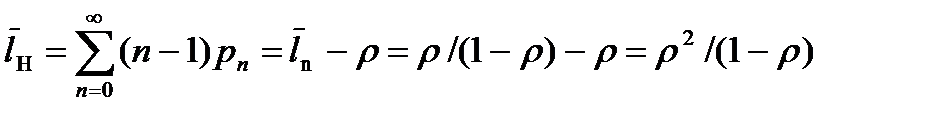 .
.
Среднее время ожидания заявок в накопителе
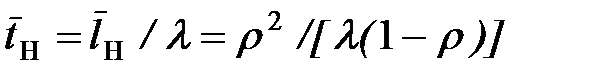 .
.
Наиболее часто для анализа Q-схем используют имитационные методы. В этом случае формализованное описание системы массового обслуживания представляет собой графическое отображение (с соответствующими комментариями) элементарных приборов, клапанов, отражающих наличие управляющих воздействий, и связей между ними. На данный момент существует много программных средств, специализирующихся на создание имитационных моделей на основе Q-схем. Примерами для прикладного применения непрерывно-стохастического подхода могут служить исследования потоков поставок продукции некоторому предприятию, потоков деталей и комплектующих изделий на сборочном конвейере цеха и т.п.
4. Статистическое моделирование
Метод статистического моделирования на ЭВМ - основной метод получения результатов с помощью имитационных моделей стохастических систем, использующий в качестве теоретической базы предельные теоремы теории вероятностей.
Основа - метод статистических испытаний Монте-Карло, который базируется на использовании случайных чисел, то есть возможных значений некоторой случайной величины с заданным распределением вероятностей. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе.
Сущность метода: построение для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды и реализации этого алгоритма с использованием программно-технических средств ЭВМ.
2 области применения: 1) изучение стохастических систем; 2) решение детерминированных задач.
Результат статистического моделирования - серия частных значений искомых величин или функций, их статистическая обработка. Если количество реализаций N ® ¥, результаты устойчивы и достаточно точны.
Теоретическая основа метода статистического моделирования является пре дельнее теоремы теории вероятностей. Их значение - гарантируют высокое качество статистических оценок при числе испытаний N ® ¥. Часто приемлемые результаты могут быть получены при достаточно небольших N.
Неравенство Чебышева. Для неотрицательной случайной величины X и любого K>0 выполняется неравенство:
P(X>=K)=<M(X)/K
Теорема Бернулли. Если проводится N независимых испытаний, в каждом из которых некоторое событие А осуществляется с вероятностью p, то относительная частота появления события m/N при N ® ¥ сходится по вероятности к p, т.е. при любом e>0
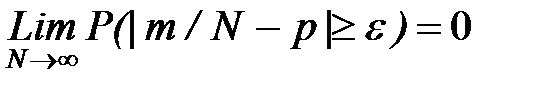 , где m - число положительных исходов испытания.
, где m - число положительных исходов испытания.
Теорема Пуассона.
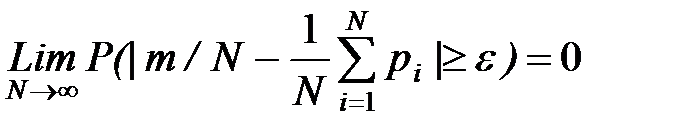 , где pi - вероятность осуществления события А в i-м испытании.
, где pi - вероятность осуществления события А в i-м испытании.
Обобщенная теорема Чебышева.
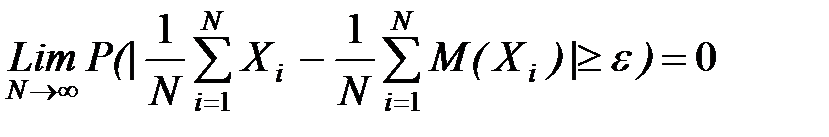 , Xi - i-ая случайная величина
, Xi - i-ая случайная величина
Теорема Маркова. Обобщенная теорема Чебышева справедлива и для зависимых случайных величин, если
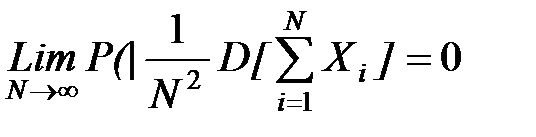
Центральная предельная теорема. Если X1 , X2,..., Xn - независимые одинаково распределенные случайные величины, имеющие математическое ожидание M(Xi)=a и дисперсию s2, то при N ® ¥ закон распределения суммы 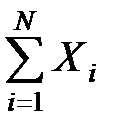 неограниченно приближается к нормальному:
неограниченно приближается к нормальному:
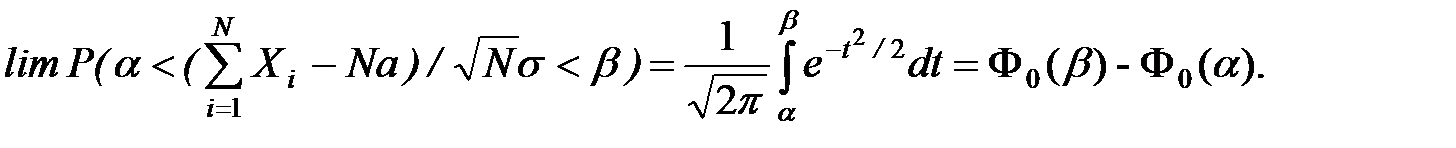
Приведем примеры применения методов статистического моделирования.
Пример 1. Входное воздействие - 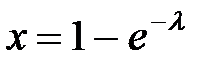 , воздействие внешней среды -
, воздействие внешней среды - 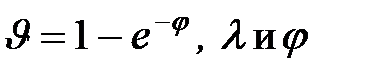 - случайные величины с известными функциями распределения.
- случайные величины с известными функциями распределения.
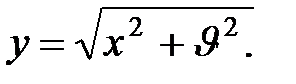 Необходимо определить математическое ожидание величины y:
Необходимо определить математическое ожидание величины y:
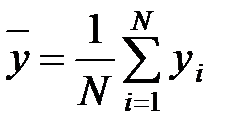
Схема алгоритма (ген. - генерация):
| i=1..N |
| ген. l |
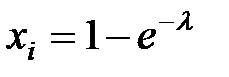
|
| ген. j |
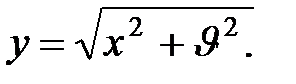
|
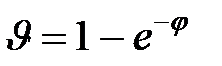
|
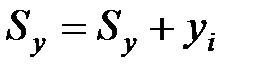
|
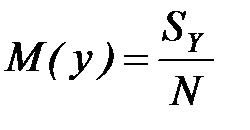
|
Пример 2. Необходимо найти площадь фигуры:
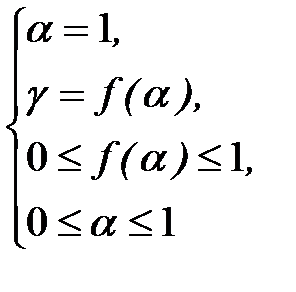
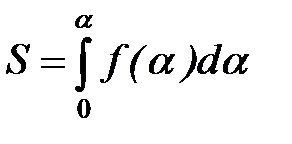
| I=1..N |
| ген. xi, xi+1 |
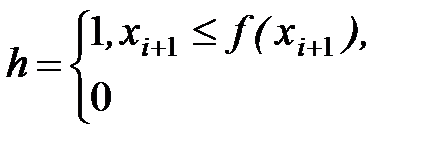
|
| S=S+h |
| S=S/N |
| I=1..N |
| ген. xi, xi+1 |
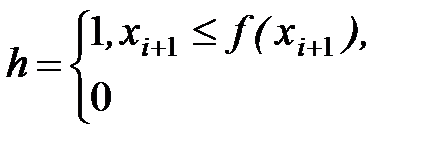
|
| S=S+h |
| S=S/N |
Аналитическое решение этой задачи:
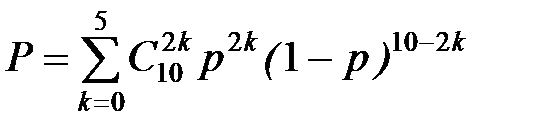
Схема алгоритма (статистическое моделирование):
| j=1..N |
| hj=0 |
| i=1..10 |
| ген. xi |
| xi < p |
| hj= hj +1 |
| hj - четн |
| S=S+hj |
| P=S/N |
Генерация последовательности случайных чисел
Существует три способа генерации случайных чисел:
1. Аппаратный - в основе лежит какой-либо физический эффект (например, шумы в электронных устройствах, случайные числа вырабатываются с помощью специального датчика. Этот способ не гарантирует качество последовательности случайных чисел непосредственно во время моделирования. С помощью этого способа нельзя получать одинаковые последовательности. Используется редко.
2. Табличные - случайные числа оформлены в виде таблицы в оперативной памяти или на внешнем носителе. При этом способе запас чисел ограничен, вычислительные ресурсы используются неэффективно. Используется редко.
3. Программный (алгоритмический) - случайные числа формируются с помощью специальных программ. Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ. Этот способ наиболее распространен.
Программная имитация случайных воздействий сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Чаще всего в качестве базовой последовательности используют независимые случайные величины, равномерно распределенные на интервале (0,1).
Непрерывная случайная величина имеет равномерное распределение в интервале (a,b), если ее функции плотности и распределения соответственно примут вид
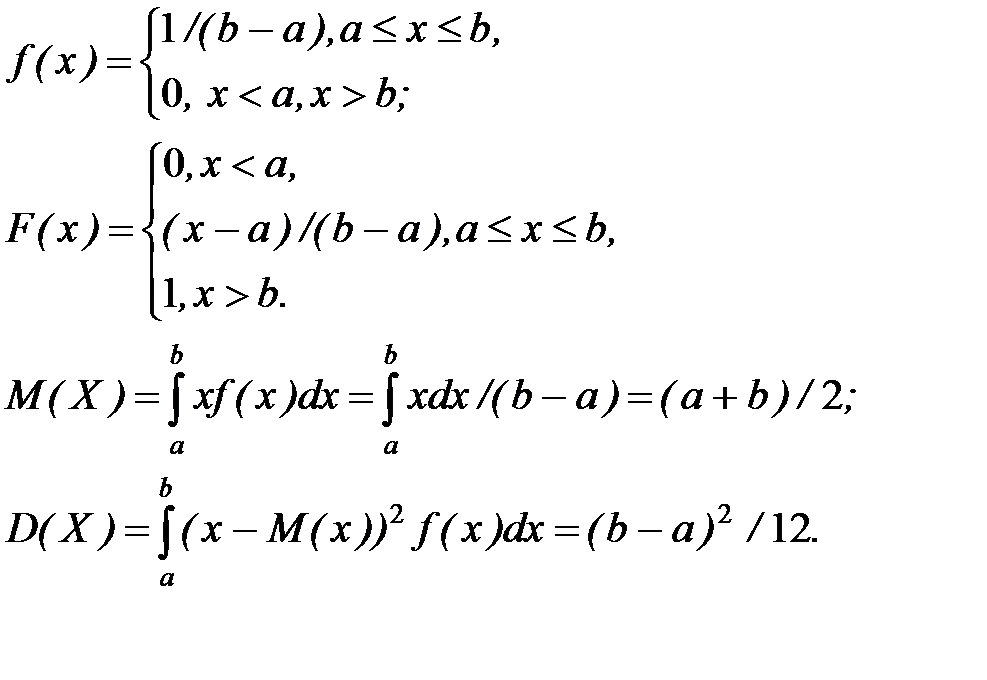
Для получения случайных чисел на ЭВМ используются алгоритмы, поэтому такие последовтельности, являющиеся по сути детерминированными, называются псевдослучайными. ЭВМ оперирует n-разрядными числами, поэтому поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2n случайных чисел того же интервала - закон распределения такой дискретной последовательности называется квазиравномерны распределением.
Требования к идеальному генератору случайных чисел:
1. Последовательность должна состоять из квазиравномернло распределенных чисел.
2. Числа должны быть независимыми.
3. Последовательности случайных чисел должны быть воспроизводимыми.
4. Последовательности должны иметь неповторяющиеся числа.
5. Последовательности должны получаться с минимальными затратами вычислительных ресурсов.
Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных числе находят алгоритмы вида:
xi+1=Ф(xi),
представляющие собой реккурентные соотношения первого порядка.
Пример. x0 = 0,2152, (x0)2=0,04631104, x1 = 0,6311, (x1)2=0,39828721, x2=0,8287 и т.д.
Недостаток подобных методов - наличие коррелляции между числами последовательности, а иногда случайность вообще отсутствует, например:
x0 = 0,4500, (x0)2=0,20250000, x1 = 0,2500, (x1)2=0,06250000, x2=0,2500 и т.д.
Широкое применение получили конгруэнтные процедуры генерации псевдослучайных последовательностей.
Два целых числа a и b конгруэнтны (сравнимы) по модулю m, где m - целое число, тогда и только тогда, когда существует такое целое число k, что a-b=km.
1984º4 (mod 10), 5008º8 (mod 103).
Большинство конгруэнтных процедур генерации случайных чисел основаны на следующей формуле:
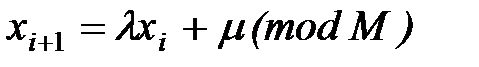
где 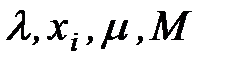 - неотрицательные целые числа.
- неотрицательные целые числа.
По целым числам последовательности {Xi} можно построить последовательность {xi}={Xi/M} рациональных чисел из единичного интервала (0,1).
Применяемые генераторы случайных чисел перед моделированием должны пройти тщательное предварительное тестирование на равномерность, стохастичность и независимость получаемых последовательностей случайных чисел.
Методы улучшения качества последовательностей случайных чисел:
1. Использование рекуррентных формул порядка r:
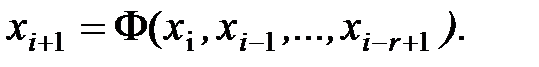
Но применение этого способа приводит к увеличению затрат вычислительных ресурсов на получение чисел.
2. Метод возмущений:
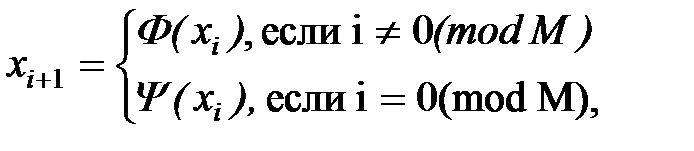
Моделирование случайных воздействий на системы
1. Необходимо реализовать случайное событие А, наступающее с заданной вероятностью p. Определим А как событие, состоящее в том, что выбранное значение xi равномерно распределенной на интервале (0,1) случайной величины удовлетворяет неравенству:
xi =<p.
Тогда вероятность события А будет 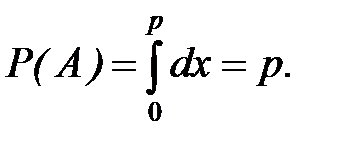 Противоположное событие состоит в том, что xi >p, его вероятность равна 1-р.
Противоположное событие состоит в том, что xi >p, его вероятность равна 1-р.
2. Рассмотрим группу событий. Пусть А1, А2 ,..., Аs - полная группа событий, наступающих с вероятностями p1, p2 ,..., ps соответственно. Определим событие Аm как событие, состоящее в том, что выбранное значение xi случайной величины удовлетворяет неравенству
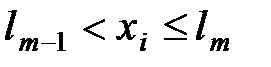 ,
,
где 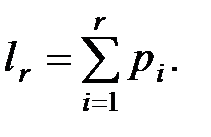
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел xi со значениями lr. Если условие выполняется, исходом испытания оказывается событие Аm.
3. Рассмотрим независимые события А и В с вероятностями наступления рА и рВ. Возможными исходами совместных испытаний в этом случае будут события АВ, 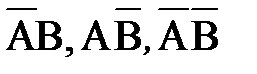 с вероятностями рАрВ, (1-рА)рВ, рА(1-рВ), (1-рА)(1-рВ). Для моделирования совместных испытаний можно использовать два варианта процедуры:
с вероятностями рАрВ, (1-рА)рВ, рА(1-рВ), (1-рА)(1-рВ). Для моделирования совместных испытаний можно использовать два варианта процедуры:
- Последовательное выполнение процедуры, рассмотренной в п.1.
- Определение одного из исходов АВ, 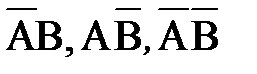 по жребию с соответствующими вероятностями, т.е. процедура, рассмотренная в п.2.
по жребию с соответствующими вероятностями, т.е. процедура, рассмотренная в п.2.
Первый вариант потребует двух чисел xi и двух сравнений. При втором варианте можно обойтись одним числом xi, но сравнений может потребоваться больше. С точки зрения удобства построения моделирующего алгоритма и экономии количества операций и памяти ЭВМ более предпочтителен первый вариант.
4. События А и В являются зависимыми и наступают с вероятностями pА и pВ . Обозначим через pА(В) условную вероятность наступления события В при условии, что событие А произошло. Алгоритм модели подобного случая может быть следующим:
| ген. xi |
| xi < pA |
| КА=КА+1 |
| ген. xi+1 |
| xi <pA(В) |
| КАВ=КАВ+1 |
| КАNВ=КАNВ+1 |
| КNА=КNА+1 |
| ген. xi+1 |
| xi <pNA(В) |
| КNАВ=КNАВ+1 |
| КNАNВ=КNАNВ+1 |
Моделирование дискретных случайных величин
Дискретная случайная величина Y принимает значения y1 <= y2 <=… <= yj <=… с вероятностями p1, p2, …, pj,… составляющими дифференциальное распределение вероятностей
| Y | y1 | y2 | … | yj | … |
| P | p1 | p2 | … | pj | … |
При этом интегральная функция распределения
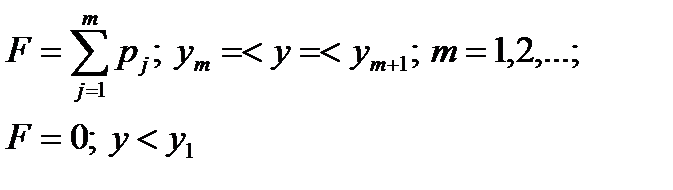
Длля получения дискретных случайных величин можно воспользоваться методом обратных функций: если X – равномерно распределенная на интервале (0,1) случайная величина, то искомую случайную величину получают при выполнении следующих действий:
Если x1 < p1 , то Y= y1 , иначе,
Если x1 < p1 + p2, то Y= y2 , иначе,
…………………………………..
Если x1 < 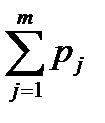 , то Y= ym, иначе,
, то Y= ym, иначе,
……………………………………
Дискретное распределение (общий случай). Предположим, что известны частоты а, выбора из N объектов на определенном интервале времени, i =1,..., N. Пример таких частот для N=7 представлен в табл. 1.3. Первая строка таблицы - это номер объекта, а вторая - частота его выбора. Требуется разработать программную функцию, которая должна возвращать значение номера объекта в соответствии
Таблица 1
Date: 2015-07-17; view: 2484; Нарушение авторских прав