Оптимизация объекта (системы) на базе его (ее) математической модели

Оптимизация – процесс поиска набора влияющих факторов, обеспечивающих экстремум критерия оптимальности с учетом ограничений первого и второго рода.

Ограничение 1 рода – это ограничение, которое накладывается на значения влияющих факторов.

Ограничение 2 рода – это ограничение, которое накладывается на значение функции отклика.

Под критерием оптимальности понимается один из параметров качества объекта (системы) или один из параметров, характеризующих процесс (производительность, выход готового продукта, удельные энергозатраты).

В некоторых случаях нельзя ограничиться одним параметром для назначения критерия оптимальности, в этом случае используется синтетический критерий, учитывающий необходимые параметры.

Методы оптимизации:

1. Метод крутого восхождения (наискорейшего спуска), часто называемый градиентным методом.

2. Симплексный метод.

В некоторых случаях при небольшом числе влияющих факторов можно воспользоваться анализом поверхности отклика путем построения плоских сечений.

Суть метода плоских сечений заключается в том, что фиксируются все влияющие факторы, кроме двух с последующим построением на плоскости линии равного отклика.

Выражение для функции отклика:

y = f (x ₁, x ₂ ,..., x_i,..., x_n)

y = f (x ₁, x ₂ )

y = f (x ₁, x ₃ )

...

y = f (x_{i- 1}, х_i)

...

y = f (x_{n- 1}, х_n)

Характерные виды плоских сечений:

y = f (x ₁, x ₂)

x₂ = φ (y, x₁ )

3. Метод крутого восхождения (наискорейшего спуска).

Этот метод широко распространен, когда математическое описание представлено в виде уравнения регрессии.

Алгоритм метода:

1. Получение описания (уравнения регрессии)

2. Определение шага варьирования по базовому фактору в процессе оптимизации.

Базовый фактор – 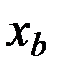. 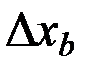– шаг варьирования.

Шаг варьирования по базовому фактору, как правило, равен шагу варьирования при получении уравнения регрессии:

,

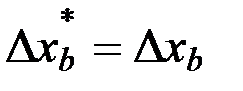где 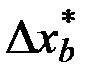– шаг варьирования в процедуре поиска по методу уравнения регрессии.

3. Определение шага варьирования по каждому из факторов.

Для этого первоначально определяется параметр .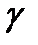

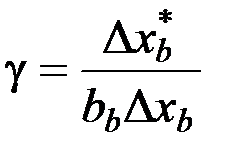
Учитываем, что 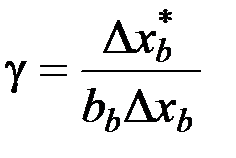должно соблюдаться для каждого , т.е. параметр 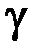является постоянным для всех влияющих факторов, тогда 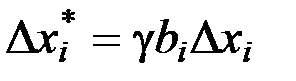– шаг варьирования для каждого фактора.

4. Вычисляют значение функции отклика при наборе влияющих факторов, получивших приращение.

y = f (x ₁ ^*, x ₂ ^*,..., x_i^*,..., x_n^*)

где 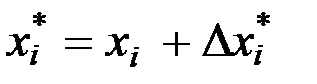, 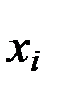– значение влияющего фактора на предыдущем шаге оптимизации. В качестве исходного первоначального значения 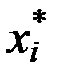принимают значение в центре плана (где проводился эксперимент). Движение осуществляют до тех пор, пока не будет достигнуто значение экстремума, либо будут достигнуты ограничения 1 или 2 рода.

Если экстремум (или ограничение) достигнут за пределами плана, то необходимо произвести вблизи экстремума проверку на адекватность (например, с использованием критерия Фишера). Если адекватность подтверждена, то процедура оптимизации закончена. Если адекватность не подтверждена, то необходимо получение нового математического описания в районе экстремума функции отклика или достигнутых ограничений 1 или 2 рода. В этой области снова строится ПФЭ, но как правило это приводит к неуспеху. Тогда строят математическое описание на базе планов более высоких порядков. После того, как получена новая адекватная модель процедура движения к оптимуму (к экстремуму или ограничениям) возобновляется, но уже на базе новой модели. Если в конечной точке процесса оптимизации не обеспечивается адекватность, то применяют планы еще более высоких порядков. В целом процесс оптимизации продолжается до тех пор, пока в зоне экстремума или ограничений не будет подтверждена адекватность модели.

В подавляющем большинстве случаев успешный поиск оптимума реализуется на базе планов не выше второго порядка.

Блок схема реализации алгоритма:

2. Симплексный метод.

Суть симплексного метода включает следующие процедуры:

1) Построение исходного симплекса (обычно в центре плана).

Симплекс – это многогранник с количеством вершин n +1, где n – количество влияющих факторов (независимых переменных).

Обычно координаты вершин симплекса располагают на границе плана.

2) Отбрасывается вершина симплекса, соответствующая наихудшему значению функции отклика и строится симметричная вершина. Процедура продолжается до тех пор, пока симплекс не зациклится.

На нижеследующем рисунке представлена графическая схема оптимизации с использованием симплексного метода для двухфакторного эксперимент. Для данного случая симплекс являет собой треугольник.

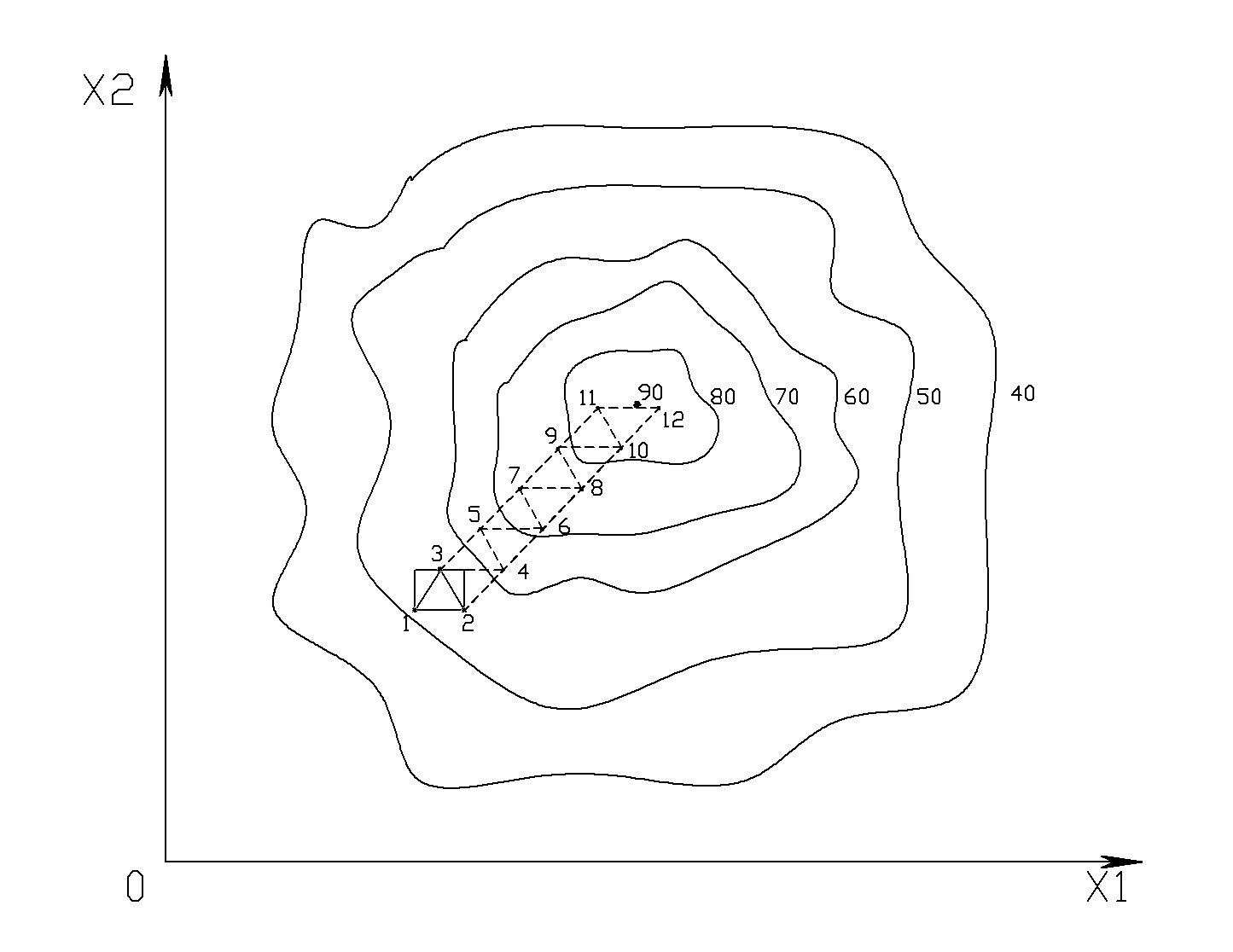
Как и в случае применения метода крутого восхождения или наискорейшего спуска в зоне предполагаемого оптимума требуется произвести проверку на адекватность математической модели и, в случае необходимости, произвести ее уточнение. Процедура может выполняться многократно до получения адекватной модели в зоне оптимума.

Процедура поиска симметричной вершины симплекса, как и процедура построения исходной вершины симплекса в общем случае для n -мерного факторного пространства базируется на аналитических зависимостях, приводимых в литературе.

Достоинства симплексного метода:

- оптимум не зависит от выбора симплекса;

- грубый промах не приведет к искажению результата.

Феноменологические модели (ФМ)

Базируются на физических представлениях о механизмах процесса. Обычно строятся на основе дифференциальных уравнениях, описывающих физическую картину процесса.

Достоинства:

- хорошие прогностические возможности в широком диапазоне влияющих факторов;

- можно использовать не проводя эксперимента.

В основе ФМ лежат математические описания.

Обычно такие модели возможно создавать для систем и процессов, описывающих фрагменты природных явлений, технологических процессов в химческой технологии, пищевой, фармацевтической промышленности, энергетике.

Для математических описаний феноменологического характера характерен принцип изоморфности описаний (от греч. isos — равный, одинаковый и греч. morphe — форма). Принцип изоморфности состоит в том, что различные явления природы могут описываться одинаковыми по форме дифференциальными уравнениями. Например:

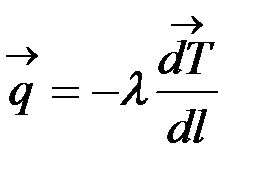
– уравнение Фурье (стационарное) – выражает плотность потока тепла,

где Т – потенциал переноса тепла (температура); l – направление переноса; λ – коэффициент теплопроводности.

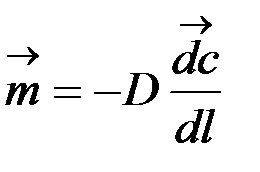
– уравнение Фика – определяет плотность потока массы,

где с – потенциал переноса массы (концентрация), D - коэффициент диффузии.

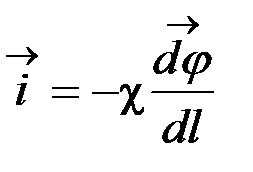
– плотность электрического тока,

где 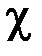– коэффициент электропроводности, 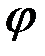– потенциал переноса электрического заряда (электрический потенциал).

Математическая модель должна быть традуктивной (обладать свойством традуктивности, см. вышеизложенные разъяснения).

Традуктивность феноменологических моделей обеспечивается соблюдением принципов подобия. Принципы подобия формируются в рамках теории подобия. Один из основных принципов теории подобия – выделение из класса явлений (объектов) группы подобных тел.

Подобными принято называть явления (объекты), для которых постоянно некоторое отношение, характеризующих их величин.

При выделении группы подобных явлений в первую очередь выявляется наличие их геометрического подобия.

Date: 2015-07-17; view: 1861; Нарушение авторских прав