
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Использование моделирования при исследовании и проектировании сложных систем
|
|
Одна из проблем современной науки и техники — разработка и внедрение в практику проектирования новейших методов исследования характеристик сложных информационно-управляющих и информационно-вычислительных систем различных уровней (например, автоматизированных систем научных исследований и комплексных испытаний, систем автоматизации проектирования, АСУ технологическими процессами, а также интегрированных АСУ, вычислительных систем, комплексов и сетей, информационных систем, цифровых сетей интегрального обслуживания и т. д.). При проектировании сложных систем и их подсистем возникают многочисленные задачи, требующие оценки количественных и качественных закономерностей процессов функционирования таких
систем, проведения структурного алгоритмического и параметрического их синтеза.
Особенности разработки систем. С истемы информатики и вычислительной техники, автоматизированные системы обработки информации и управления, информационные системы относятся к классу больших систем, этапы проектирования, внедрения, эксплуатации и эволюции которых в настоящее время невозможны без использования различных видов моделирования. На всех перечисленных этапах для сложных видов различных уровней необходимо учитывать следующие особенности: сложность структуры и стохастичность связей между элементами, неоднозначность алгоритмов поведения при различных условиях, большое количество параметров и переменных, неполноту и недетерминированность исходной информации, разнообразие и вероятностный характер воздействий внешней среды и т. д. Ограниченность возможностей экспериментального исследования больших систем делает актуальной разработку методики их моделирования, которая позволила бы в соответствующей форме представить процессы функционирования систем, описание протекания этих процессов с помощью математических моделей, получение результатов экспериментов с моделями по оценке характеристики исследуемых объектов. Причем на разных этапах создания и использования перечисленных систем для всего многообразия входящих в них подсистем примение метода моделирования преследует конкретные цели, а эффективность метода зависит от того, насколько грамотно разработчик использует возможности моделирования.
Независимо от разбиения конкретной сложной системы на подсистемы при проектировании каждой из них необходимо выполнить внешнее проектирование (макропроектирование) и внутреннее проектирование (микропроектирование). Так как на этих стадиях разработчик преследует различные цели, то и используемые при этом методы и средства моделирования могут существенно отличаться.
На стадии макропроектирования должна быть разработана обобщенная модель процесса функционирования сложной системы, позволяющая разработчику получить ответы на вопросы об эффективности различных стратегий управления объектом при его взаимодействии с внешней средой. Стадию внешнего проектирования можно разбить на анализ и синтез. При анализе изучают объект управления, строят модель воздействий внешней среды, определяют критерии оценки эффективности, имеющиеся ресурсы, необходимые ограничения. Конечная цель стадии анализа — построение модели объекта управления для оценки его характеристик. При синтезе на этапе внешнего проектирования решаются задачи выбора стратегии управления на основе модели объекта моделирования, т. е. сложной системы.
На стадии микропроектирования разрабатывают модели с целью создания эффективных подсистем. Причем используемые методы и средства моделирования зависят от того, какие конкретно обеспечивающие подсистемы разрабатываются: информационные, математические, технические, программные и т. д.
Особенности использования моделей. Выбор метода моделирования и необходимая детализация моделей существенно зависят от этапа разработки сложной системы. На этапах обследования объекта управления, например промышленного предприятия, и разработки технического задания на проектирование автоматизированной системы управления модели в основном носят описательный характер и преследуют цель наиболее полно представить в компактной форме информацию об объекте, необходимую разработчику системы.
На этапах разработки технического и рабочего проектов систем, модели отдельных подсистем детализируются, и моделирование служит для решения конкретных задач проектирования, т. е. выбора оптимального по определенному критерию при заданных ограничениях варианта из множества допустимых. Поэтому в основном на этих этапах проектирования сложных систем используются модели для целей синтеза.
Целевое назначение моделирования на этапе внедрения и эксплуатации сложных систем — это проигрывание возможных ситуаций для принятия обоснованных и перспективных решений по управлению объектом. Моделирование (имитацию) также широко применяют при обучении и тренировке персонала автоматизированных систем управления, вычислительных комплексов и сетей, информационных систем в различных сферах. В этом случае моделирование носит характер деловых игр. Модель, реализуемая обычно на ЭВМ, воспроизводит поведение управляемого объекта и внешней среды, а люди в определенные моменты времени принимают решения по управлению объектом.
Математические модели делятся на:
1. Феноменологические (явленческие). Часто такие модели называют аналитическими.
2. Статистические.
Феноменологические модели строятся на базе физических моделей. Эти модели в построении и использовании более предпочтительны. Они описывают объект в широком диапазоне влияющих факторов. Использование этих моделей дает представление о физических процессах. Они обладают широкими прогностическими возможностями. Недостатком этих моделей является невысокая точность, которая объясняется множеством допущений. Этот недостаток может быть скомпенсирован посредством оперативной подстройки параметров моделей.
Статистические модели строятся на базе первичной информации, полученной эмпирическим (экспериментальным) путем. Статистические модели создаются в случае, когда мало известно о внутренних свойствах процесса.
Статистические модели. (СМ)
Эмпирическая информация может быть получена на базе оригинала или на базе реального объекта.
Во многих случаях СМ рассматривается в виде черного ящика (Ч.Я.).
Понятие Ч.Я.

Здесь хi – входные параметры модели (влияющие факторы);
yj – выходные параметры (функции отклика)
zk – неконтролируемые входные параметры (фоновые, шумовые факторы)
Ч.Я. – это объект, о внутреннем устройстве которого и процессах, происходящих внутри которого, нам ничего не известно, и о свойствах которого судят, установив зависимость между входными и выходными параметрами. При этом шумовые параметры не должны превышать допустимых пределов.
Разновидности статистических моделей:
1. Модели, полученные в рамках корреляционного анализа. Корреляционный анализ – это совокупность хорошо разработанных методов (одна из областей математического анализа). Корреляционный анализ применяется при необходимости установления связи между двумя или большим количеством параметров, каждый из которых подвергается случайному неконтролируемому рассеиванию (имеет неконтролируемую дисперсию). В рамках корреляционного анализа устанавливается связь (не жесткая) между хi и yj.
Коэффициент корреляции 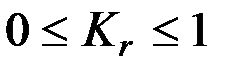 .
.
Если Kr =0, то говорят, что связи между параметрами нет.
Если Kr =1, то говорят о полной функциональной зависимости.
Корреляция отличается от функции тем, что между параметрами нет жесткой связи.
2. Модели, строящиеся на базе дисперсионного анализа. Применяются тогда, когда требуется определить какова существенность влияния того или иного фактора на функцию отклика.
При использовании дисперсионного анализа значение функции отклика может приобретать ряд (спектр) значений, которые проявляются случайным образом и могут быть описаны только на базе теории вероятности. Случайные величины полностью характеризуются функцией плотности вероятности распределения случайной величины (дифференциальная функция распределения) или функцией, описывающей вероятность вхождения в интервал (интегральная функция распределения).
Спектр случайной величины может быть охарактеризован (не полностью) рядом моментов случайных величин, к таковым начальный момент
 ,
,
центральный момент
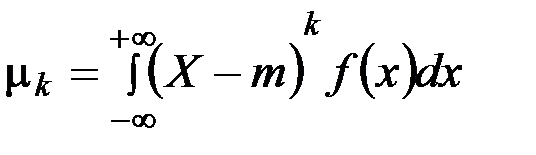
и другие.
Наибольшее значение при описании случайной величины имеют первый начальный момент (матожидание):
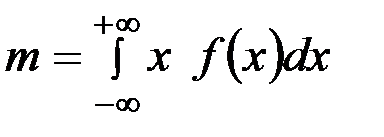 ;
;
и второй центральный момент (дисперсия):
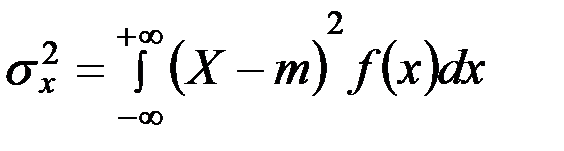 .
.
Матожидание – это наиболее часто встречающаяся вероятность (расположение центра распределения).
Дисперсия же характеризует в определенной степени область распределения.
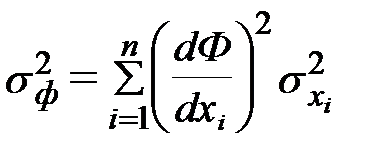
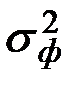 -дисперсия функции.
-дисперсия функции.
3. Модели на базе регрессионного анализа. Регрессионный анализ создавался для металлургии, затем распространялся в другие области. Метод регрессионного анализа позволяет получить описание функции отклика, как функций многих переменных (n -факторное пространство) и четко отвечает на вопрос о требуемом количестве экспериментов, на базе результатов которых формулируется математическая модель.
В результате регрессионного анализа получают функциональную зависимость в форме уравнения регрессии. Уравнение регрессии представляет собой отрезок ряда Тейлора:
Y=b0+b1x1+b2x2+...+bjxj+...+bnxn+b12x1x2+...+blkxlxk+...+b(n-1)nxn-1 xn+
+...+b11x12+b22x22+...+bjjxj+...bnnxn2+...
 ;
; 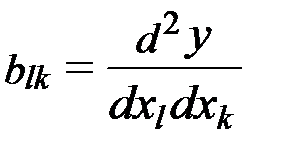 ;
; 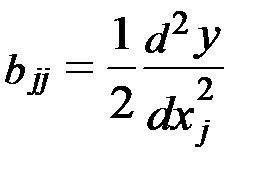 .
.
Коэффициенты, входящие в состав уравнения находят на базе экспериментальных данных.
Простейший метод получения уравнения регрессии, когда поверхность отклика имеет незначительную кривизну, носит название метода полного факторного эксперимента (ПФЭ). Этот метод, как и весь регрессионный анализ базируется на анализе теории рядов, метода наименьших квадратов. ПФЭ позволяет определить  необходимое и достаточное количество экспериментов, построить математическое описание процесса в форме уравнения регрессии, содержащего свободный член b0, члены первого порядка bjxj и члены, характеризующие парные взаимодействия blk xl xk. Члены второго порядка отсутствуют
необходимое и достаточное количество экспериментов, построить математическое описание процесса в форме уравнения регрессии, содержащего свободный член b0, члены первого порядка bjxj и члены, характеризующие парные взаимодействия blk xl xk. Члены второго порядка отсутствуют 
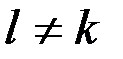 . При приведении ПФЭ варьирование влияющих факторов осуществляется только на двух уровнях: верхнем и нижнем. Для того чтобы определить значения влияющих факторов на верхнем и нижнем уровне необходимо определить эти значения на базовом уровне (координаты центра плана).
. При приведении ПФЭ варьирование влияющих факторов осуществляется только на двух уровнях: верхнем и нижнем. Для того чтобы определить значения влияющих факторов на верхнем и нижнем уровне необходимо определить эти значения на базовом уровне (координаты центра плана).
Зачастую проведение экспериментов в рамках регрессионного анализа называют проведением планированных экспериментов, а подготовку к проведению экспериментов называют планированием эксперимента.
План – это область, ограниченная значениями влияющих факторов, имевших место при проведении эксперимента с целью получения информации для расчета коэффициентов в уравнении регрессии. Эксперимент такого рода называется планированием эксперимента.
Базовые значения влияющих факторов (значения на базовом уровне) обычно назначают в хорошо исследованной зоне или, если таковая отсутствует, проводится экспертная оценка базовых факторов, базирующаяся на интуиции, опыте исследователей. Общее обозначение базовых значений параметра: x0i. Тогда 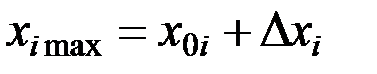 ,
,  ; где
; где 
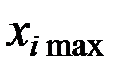 – значение на верхнем уровне;
– значение на верхнем уровне;  –значение на нижнем уровне;
–значение на нижнем уровне; 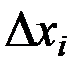 – шаг варьирования, определяется обычно как доля базового уровня:
– шаг варьирования, определяется обычно как доля базового уровня: 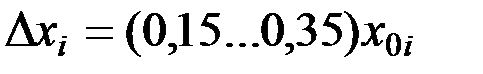
Далее надлежит построить матрицу планирования. При формировании матрицы планирования значения влияющих факторов представляют в безразмерной (кодированной) форме.
Запишем формулу перехода от размерной к безразмерной форме:
Безразмерные переменные будем обозначать X.
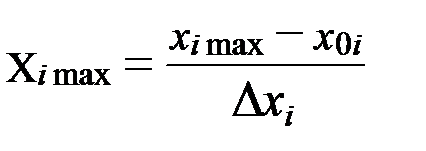 ,
, 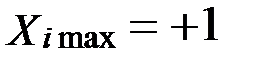 – верхний уровень,
– верхний уровень,
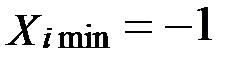 – нижний уровень.
– нижний уровень.
Для формирования матрицы планирования необходимо определить количество необходимых и достаточных опытов N:
N =2 n, где n – количество влияющих факторов.
Пример матрицы планирования.
Пусть в качестве функции отклика фигурирует величина скорости работы компьютера. Доопытно пусть будет, что скорость зависима от производительности процессора, объема оперативной памяти и скорости воспроизведения (записи) инфпрмации жесткого диска. Эксперимент будем вести по методу ПФЭ. Пусть в каждой строке матрицы отражаются величины независимых параметров, влияющих факторов и функций откликов, характеризующие j -ый эксперимент. Количество строк в этом случае будет равно 8.
Задание частоты варьирования влияющих факторов.
Установлено следующее правило: для первого (базового) фактора частота варьирования определяется изменением уровня от опыта к опыту, частота варьирования каждого последующего фактора в 2 раза меньше, чем у предыдущего.
Матрица планирования.
| N | х1 | х2 | х3 | X1 | X2 | X3 | X1 X2 | X1 X3 | X2 X3 | yjэ | yj р | sад 2 |
| 0.48 | +1 | +1 | +1 | +1 | +1 | +1 | ||||||
| 0.32 | -1 | +1 | +1 | -1 | +1 | |||||||
| 0.48 | +1 | -1 | +1 | -1 | +1 | -1 | ||||||
| 0.32 | -1 | -1 | +1 | +1 | -1 | -1 | ||||||
| 0.48 | +1 | +1 | -1 | +1 | -1 | -1 | ||||||
| 0.32 | -1 | +1 | -1 | -1 | +1 | -1 | ||||||
| 0.48 | +1 | -1 | -1 | -1 | -1 | +1 | ||||||
| 0.32 | -1 | -1 | -1 | +1 | +1 | +1 |
Прежде, чем начать эксперимент необходимо убедиться в воспроизводимости эксперимента. Воспроизводимость эксперимента определяют на базе специальной серии опытов. Для этого составляется специальная небольшая матрица, которая выглядит следующим образом:
| K Np | ... | l | ... | k | < y j > | s yj 2 | ||
| ... | ... | |||||||
| ... | ... | |||||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| j | ... | yjl | ... | |||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| Nn | ... | ... | ||||||
Эта матрица содержит Np строк, где Np – количество серий параллельных опытов, K – кол-во параллельных опытов в рамках серии. Обычно на практике Np = K =2 или 4.
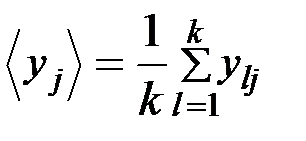

f - количество степеней свободы при определении дисперсии. В нашем случае f = k -1. f определяется как количество параллельных опытов за вычетом числа величин, используемых в определении параметра (дисперсии) и рассчитанных ранее на базе опытов. После определения дисперсии для каждой серии опыта определяем расчетное значение критерия Кохрена:
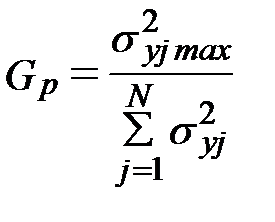 .
.
После определения расчетного значения критерия Кохрена определяют табличное значение критерия Кохрена –  . (определяем по таблицам параметры Np и f). Если воспроизводимость экспериментов доказана, т.е
. (определяем по таблицам параметры Np и f). Если воспроизводимость экспериментов доказана, т.е 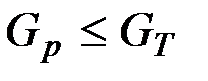 , то эксперименты считаются воспроизводительными и при реализации опыта в соответствии с реализованной матрицей планирования дублирование экспериментов не обязательно. Если воспроизводимость не доказана, то необходим анализ ситуации, почему не наблюдается воспроизводимость. Причинами невоспроизводимости могут быть:
, то эксперименты считаются воспроизводительными и при реализации опыта в соответствии с реализованной матрицей планирования дублирование экспериментов не обязательно. Если воспроизводимость не доказана, то необходим анализ ситуации, почему не наблюдается воспроизводимость. Причинами невоспроизводимости могут быть:
1. Неквалифицированный исследователь.
2. Негодное оборудование.
3. Неучтен сильный влияющий фактор (например, катализатор и др.).
4. Ищут зависимость там, где ее нет.
Date: 2015-07-17; view: 1400; Нарушение авторских прав