Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод дробного факторного эксперимента
|
|
Метод дробного факторного эксперимента – система опытов, представляющая собой часть ПФЭ, позволяющая рассчитать значения коэффициентов уравнения регрессии и уменьшить объем экспериментальных работ.
Суть метода состоит в том, что одну из переменных (независимую) заменяют величиной парного взаимодействия. Xi=XlXk. При этом возникают проблемы. Суть проблемы – выбрать произведение XlXk, которое не будет являться значимым, т.е. будет иметь незначимые члены уравнения регрессии.
Запись Xi=XlXk носит название генерирующего соотношения, обычно выбирается самим экспериментатором.
Число опытов в случае ДФЭ определится:
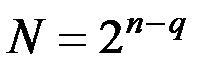,где q – количество генерирующих соотношений.
В случае, когда построенная по методу ПФЭ регрессионная математическая модель не является адекватной (большая кривизна поверхности), следует ввести в рассмотрение члены ряда Тейлора (члены уравнения регрессии) более высоких порядков.
Известны следующие методы планирования экспериментов (регрессионного анализа), позволяющие определить коэффициенты при членах второго порядка:
1. Ортогональное, центральное, композиционное планирование.
2. Рототабельное центр. композиционное планирование.
Суть методов: кроме варьирования на верхнем и нижнем уровнях эксперименты осуществляется в центре плана (на базовом уровне) и в так называемых звездных точках за пределами плана ПФЭ.
Ценность статистических моделей:
1. Модель позволяет с высшей точностью описать процесс в области адекватности, в любых точках зоны адекватности (где проводились эксперименты). За пределами области адекватности модель требует дополнительного изучения.
2. Модель может служить основой для оптимизации. Дает возможность описать математически процесс, когда невозможно создать феноменологическую модель.
Date: 2015-07-17; view: 641; Нарушение авторских прав