Определение коэффициентов уравнения регрессии

Некоторые свойства матрицы планирования:

1. Сумма всех безразмерных значений параметров.

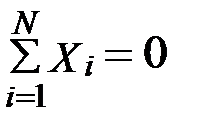
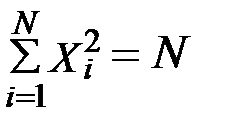
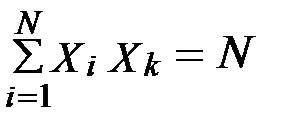
Эти свойства положены в основу расчета коэффициентов уравнения регрессии. При определении выражений для коэффициентов используется метод наименьших квадратов. К данному случаю метод наименьших квадратов запишется:

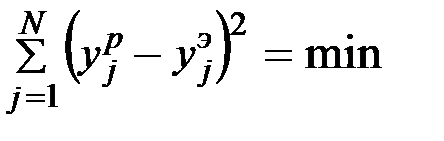
Для свободного члена: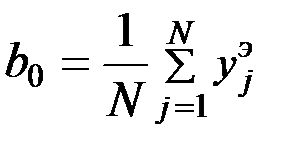

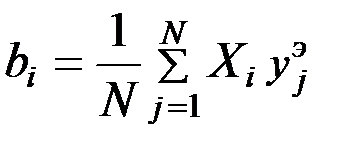
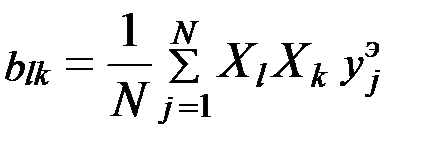
После определения значения коэффициентов в уравнении регрессии производится проверка значимости коэффициентов по условию: 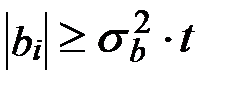, где

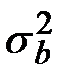– оценка дисперсии, с которой определяются коэффициенты.

, где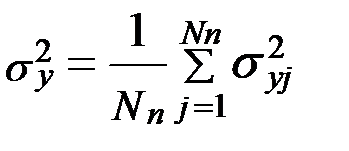

t – критерий Стьюдента.

Критерий Стьюдента находят из таблиц – по количеству степеней свободы и некоторой доверительной вероятности. Если коэффициент оказался незначимым, то его считают равным нулю, т.е. он исчезает из уравнения регрессии.

Далее проводится проверка адекватности модели (соответствие модели). Условие проверки: критерий Фишера – расчетный должен быть меньше или равен табличному.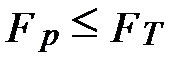

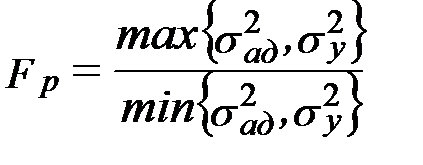(1)

Если нет проверки на воспроизводимость, то используют вместо формулы (1) используют формулу 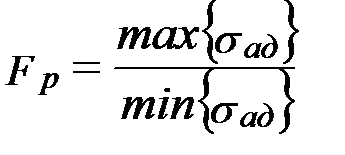(2):

(2)

Дисперсия адекватности: ,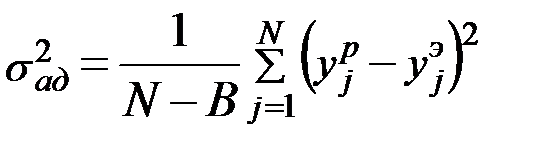

где B – число значимых коэффициентов в уравнении регрессии, включая свободный член. Если коэффициент оказался незначимым (равен 0), то данный фактор не является влияющим).

Date: 2015-07-17; view: 483; Нарушение авторских прав