При нормальном распределении 2 page

Задавшись уровнем достоверности, относительной (абсолютной) погрешностью, предполагаемым сроком службы, режимом испытаний, а также пользуясь полу­ченными графической и аналитической (эмпирической) зависимостями, определяют объем испытаний и степень ускорения. Объем испытания существенно зависит от предполагаемого срока службы РЭА.

Недостатком рассмотренной программы подготовки к проведению ускоренных испытаний является ее дли­тельность.

Предложенная последовательность работ справедли­ва при проведении испытании любых элементов и аппаратов. Однако установление интересующих нас зависи­мостей для сложных РЭА или систем оказывается дли­тельным и трудоемким процессом. Поэтому, если пред­положить, что надежность элементов РЭА не зависит от их взаимодействия и законы распределения отказов у них одинаковы и экспоненциальны, то закон распре­деления отказов РЭА будет также экспоненциальным при всех принятых допущениях.

Отсюда оказывается возможным во многих случаях на основании испытаний элементов сделать вывод о на­дежности РЭА в целом.

Рассмотрим ряд примеров, показывающих, как, поль­зуясь экспериментальными или аналитическими зави­симостями, можно выбрать режим ускоренных испыта­ний различных радиоэлементов.

Известно, что надежность электровакуумных прибо­ров зависит от внешних условий эксплуатации и от электрических режимов аппарата. Основными парамет­рами, характеризующими электрические режимы, явля­ются коэффициент электрической нагрузки, напряжение накала и напряжения на аноде и экранной сетке. Коэф­фициентом электрической нагрузки электронных ламп называют отношение суммарной мощности рассеивания на электродах к суммарной допустимой мощности рас­сеивания:

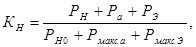(3)

гдеР_Н - реальная мощность накала;

Р_а, Р_Э - реальные мощности рассеивания на аноде и экранной сетке;

Р_макс.а, Р_макс.Э - максимальные мощности рассеивания на аноде и экранной сетке;

Р_Н0 - номинальная мощность накала.

Очевидно, что в нормальном режиме при коэффици­енте нагрузки К_Н=1 средний срок службы лампы ра­нен Т₁. Увеличение мощности, рассеиваемой на электро­дах лампы, т. е. работа при перегрузке, приводит к со­кращению среднего срока службы лампы до Т₂ и росту интенсивности отказов.

Наличие зависимости относительного изменения среднего срока службы (Т₂/ Т₁) лампы от коэффициента погрузки (К_Н) позволяет установить степень надежности лампы (рисунок 3).

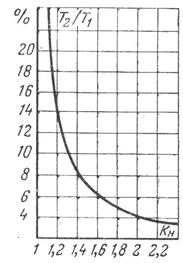
Рисунок 3 – Зависимость относительного изменения среднего срока службы сверхминиатюрных ламп от коэффициента нагрузки

Если относительное изменение среднего срока службы при увеличении К_Н оказывается больше допустимого значения, то надежность лампы выше заданной. В противном случае лампа оказывается ненадежной. Так, например, из графика на рисунке 3 следует, что при увеличении К_Н на 20% (К_Н=1,2) T₂/T₁= =14%. Это означает, что средний срок службы сокра­щается в семь раз (100/14»7). Следовательно, если при К_Н=1,2 T₂/T₁ >14%, то лампа в нормальном режиме будет работать в течение вре­мени T₁. Если же в процес­се ускоренных испытаний значение T₂/T₁ <14% (при К_Н=1,2), то это свидетель­ствует о ненадежности лампы.

Знание электрической за­висимости интенсивности от­казов приемно-усилительных ламп от напряжения нака­ла позволяет осуществить ус­коренные испытания за счет увеличения напряжения на­кала. Интенсивность отказов при рабочем напряжении U_Н определяется формулой

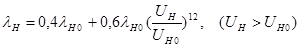(4)

где l_Н0 - интенсивность от­казов при номинальном на­пряжении накала;

U_H - рабочее напряжение накала;

U_H0 - номинальное напряжение накала.

Аналогично можно воспользоваться эмпирической формулой зависимости интенсивности отказов от анодно-экранного напряжения (U_а):

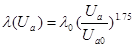, (5)

где U_а - рабочее анодно-экранное напряжение; U_а0 - номинальное анодно-экранное напряжение.

Наличие экспериментально установленной связи среднего времени безотказной работы транзисторов (П13, П16) от мощности рассеиваемой на коллектор­ном переходе и от температуры окружающей среды позволяет осуществить их ускоренные испытания:

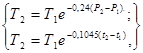, (6)

где T₁ - среднее время безотказной работы при нор­мальной мощности рассеивания (P₁) и нор­мальной температуре (t₁);

T₂ - среднее время безотказной работы при повы­шенной мощности рассеивания (P₂) и повы­шенной температуре (t₂).

Из формул следует, что увеличение мощности рас­сеивания или температуры окружающей среды приво­дит к уменьшению среднего времени безотказной рабо­ты T₂.

Одним из наиболее широко применяемых в радио­аппаратуре элементов являются резисторы (около 40% всех элементов). Интенсивность отказов резисторов в значительной степени зависит от температуры окру­жающей среды и рассеиваемой мощности. Аналитиче­ская зависимость, связывающая относительную интен­сивность отказов с температурой окружающей среды и рассеиваемой мощностью, имеет вид:

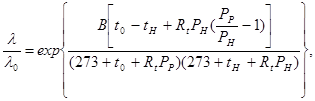(7)

где l - интенсивность отказов в рабочем режиме при реально рассеиваемой мощности (Р_р);

l₀ - интенсивность отказов при допустимой (номи­нальной) рассеиваемой мощности (Р_Н) и пре­дельно допустимой (номинальной) температуре окружающей среды (t_H);

t_P - реальная температура окружающей среды;

R_t - тепловое сопротивление теплоотдачи с поверх­ности в окружающую среду;

В - постоянная, определяемая из опыта.

В соответствии с приведенной формулой для кон­кретного типа резистора строят зависимости l/l₀ =f( t₀, Р_р/Р_Н) при определенных путем обработки статистиче­ских данных постоянных В, R_t и l₀. Пользуясь графи­ком (рисунок 4), можно найти величину в зависимости от Р_P и t_t.

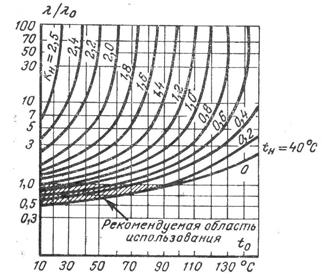
Рисунок 4 – Расчетные зависимости интенсивности отказов композиционных резисторов от температуры окружающей среды и коэффициента нагрузки

Столь же широкое применение в РЭА имеют конден­саторы, интенсивность отказов которых того же поряд­ка, что и резисторов. Интенсивность отказов конденса­торов существенно зависит от электрических режимов, температуры и влажности окружающей среды. на средний срок 'службы конден­саторов выражается следующей эмпирической, зависи­мостью:

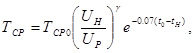(8)

где U_Н - номинальное напряжение;

U_Р реальное напряжение;

t₀ - температура окружающей среды, °С;

t_H – номинальная температура среды ^оС;

Т_ср0 – средний срок службы при номинальном напря­жении и температуре окружающей среды t₀⁰=t_H⁰;

g= 2¸4 - постоянная, определяемая из опыта для данного типа конденсаторов.

За счёт увеличения реального напряжения или тем­пературы окружающей среды возможно ускорение про­цесса испытаний конденсаторов.

Мы привели примеры возможного осуществления ускоренных испытаний при вполне определенных воздей­ствующих факторах только для ряда радиоэлементов. Установление подобных зависимостей для всех элемен­тов при воздействии различных факторов является од­ной из первоочередных задач. Когда ускоренные испы­тания элементов не являются разрушающими, а время их проведения мало, их целесообразно вводить в тех­нологический процесс.

1.6. ИСПЫТАНИЯ НА ПОВРЕЖДАЮЩУЮ НАГРУЗКУ

Испытания на повреждающую нагрузку имеют целью оценить стойкость элементов (деталей и узлов), а иногда и РЭА к внешним воздействиям. Поскольку в ходе испытаний выявляются «слабые» элементы со скры­тыми дефектами, то иногда эти испытания называют «поиском критической слабости». При этом методе ис­пытаний нагрузка (внешнее воздействие) увеличивается постепенно до момента возникновения отказа испытываемого элемента (аппарата). Величина нагрузки фик­сируется как в процессе ее увеличения, так и в момент отказа.

Иногда, при наличии большого запаса надежности, элементы и аппараты выдерживают нагрузку, во много раз превышающую максимальную, имеющую место при реальной эксплуатации. Эмпирически установлено, что испытания следует прекращать после того, как РЭА выдержит четырехкратное превышение максимально допустимого значения нагрузки. В ряде случаев возник­новение отказа не приводит к окончательному выходу из строя элемента РЭА и он после снятия нагрузки и устранения отказа оказывается вновь работоспособным.

Как указывалось, отличие испытаний на повреждаю­щую нагрузку от испытаний на срок службы заключа­ется в различной длительности испытаний.

При испытаниях на повреждающую нагрузку время безотказной работы не фиксируется и не исследуется. Для исключения побочного влияния длительности вре­мени испытаний его стараются сокращать. Как правило, испытаниям на повреждающую нагрузку чаще всего подвергают элементы (РЭА) кратковременного и одно­кратного действия, так как они работают в более тя­желых режимах.

Испытания на повреждающую нагрузку позволяют получить сведения о возможности использования эле­ментов (РЭА) при определенной нагрузке, но по их ре­зультатам нельзя определить характеристики надеж­ности.

При испытаниях узлов и РЭА необходимо быть уверенным, что используемые в них детали об­ладают требуемой надеж­ностью. Возможность воз­никновения скрытых де­фектов в деталях из-за их несовершенства маскиру­ет и осложняет анализ причин возникновения от­казов.

Элементы и РЭА мо­гут испытываться на оди­ночную и комплексную нагрузку. Чем большее количество нагрузок действует одновременно, тем условия испытании ближе к эксплуа­тационным. Однако принято, что повреждающая нагруз­ка выбирается только одна. Она действует одновремен­но с другими нагрузками нормального уровня.

Для удобства фиксации интенсивности нагрузок и параметров элементов (РЭА), а также с целью обеспе­чения времени установления стационарного режима по­вреждающая нагрузка увеличивается скачкообразно с выдержкой после каждого скачка. Величина выдерж­ки (Dt) зависит от характера нагрузки. Величина скач­ка нагрузки (Dх) устанавливается экспериментально (рисунок 5).

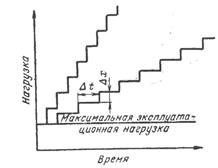
Рисунок 5 – Программа испытаний на повреждающую нагрузку

Для ускорения процесса испытаний величину скач­ка целесообразно брать большой, однако при этом воз­растает вероятность увеличения ошибки при определе­нии величины повреждающей нагрузки.

Пользуясь данными испытаний, строят гистограмму распределения повреждающей нагрузки. Для этого сна­чала составляют таблицу 1, называемую статистиче­ским рядом.

Таблица 1

В таблице 1 весь диапазон наблюденных значений х представлен разбитым на интервалы или «разряды». В таблице приняты обозначения: I_i - обозначение i-ro разряда; x_i, x_i+1 - границы разряда; k —число разря­дов; p_i- частота отказов.

В данном случае под частотой отказов будем пони­мать вероятность отказов элементов q_i

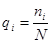, (9)

где N —начальное число испытываемых элементов;

n_i - число отказавших элементов в данном разряде.

Для построения гистограммы (рисунок 6) по оси абсцисс откладывают разряды (x_i, x_i+1), полагая, что все разряды по длине одинаковы, а по оси ординат—ве­роятность отказов элементов q_i. За начало отсчета при­нимают значение нагрузки, при котором q_i максимальна. Вправо и влево от данного значения отложены разряды больших и меньших нагрузок, при которых вероятность отказа уменьшается.

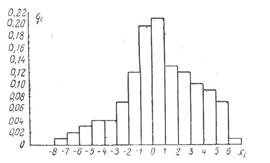
Рисунок 6 – Гистограмма распределения повреждающей нагрузки

Полная площадь построенной гистограммы равна единице. При увеличении числа интервалов (скачков) разряды становятся мельче и гистограмма приближа­ется к кривой, ограничивающей площадь, равную еди­нице. Эта кривая, представляющая собой график плот­ности распределения величины х, называется кривой распределения.

Как показывает опыт, повреждающие нагрузки ча­ще всего распределены по нормальному закону. Знание закона распределения позволяет ориентировочно ука­зать интервал практически возможных значений случай­ных нагрузок (правило трех сигм).

Имея статистические данные величины повреждаю­щей нагрузки и кривую распределения, вычисляют па­раметры закона распределения: среднюю повреждаю­щую нагрузку (математическое ожидание)

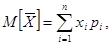(10)

где x_i - дискретная случайная величина нагрузки, имеющая возможные значения х₁, х₂,…, x_n с вероятно­стями p₁, p₂, …, р_n, и среднее квадратичное отклоне­ние повреждающей нагрузки от среднего значения

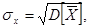(11)

гдe 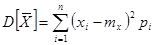- дисперсия случайной величи­ны нагрузки х, а 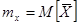- математическое ожидание.

Определение указанных выше параметров позволяет оценить некоторое среднее значение М[ 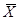] и степень рас­сеивания возможных случайных величин 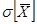около него.

1.7. СТАТИСТИЧЕСКИЕ ИСПЫТАНИЯ

Метод статистических испытаний (метод Монте-Карло) заключается в том, что при помощи многократ­ных случайных испытаний (вычислений, производимых над случайными числами) определяют вероятность по­явления некоторого случайного события (математиче­ского ожидания случайной величины).

Данный метод позволяет определить характеристики надежности исходя из предположения, что известен механизм образования отказов при различных сочетаниях значений параметров РЭА, выбираемых случайным образом согласно заданной статистической модели. При­менение этого метода позволяет путем многократного моделирования случайного процесса определить иско­мую величину. Решение поставленной задачи стало возможным только с появлением ЭВМ, позволяющих за короткое время произвести оценку влияния различных изменений параметров элементов на выходные парамет­ры РЭА. Для нахождения этого решения необходимо знание граничных параметров элементов, определяющих пределы работоспособности (А) радиоаппарата.

Статистическим испытаниям могут подвергаться как математические, так и физические модели РЭА. Метод статистического испытания математической модели базируется на знании уравнений, свя­зывающих входные параметры (x₁, х₂,..., х_n) с выход­ными параметрами испытываемого устройства (y₁, y_{2, …,} y_n). Эти уравнения могут быть выведены на основании изучения конкретной РЭА и ее внутренних функциональных связей, после чего осуществляют фор­мализацию (математическое описание установленных связей с учетом воздействия различных факторов на РЭА). Формализация заключается в составлении математических зависимостей, определяемых структура­ми элементов (РЭА) и характером их функционирова­ния. При этом необходимо правильно выбрать основные факторы, влияющие на функционирование РЭА. Увели­чение числа учитываемых факторов приводит к услож­нению моделирования РЭА. Выбрав параметры (x₁, х₂,..., х_n), характеризующие процессы функционирова­ния системы и необходимые для оценки ее эффективно­сти, и полагая, что работоспособность РЭА определя­ется набором параметров y=(y₁, y_{2, …,} y_n), построим модель процесса, определяющего вероятность попада­ния параметра y=f(x₁, x₂,…, xn), где x₁, x₂,…, xn - случайные величины, обладающие заданным распреде­лением в области работоспособности A:

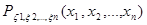(12)

Далее разрабатывают алгоритмы, моделирующие процессы функционирования РЭА. Алгоритмы (системы правил) определяют последовательность операций (ана­литических или логических), выполняемых с целью получения численных величин параметров эффективности. Алгоритмы записываются в виде математических фор­мул, схем или при помощи логического, описания. В данном случае алгоритмы функций должны обеспечи­вать получение совместного распределения (9) при известных распределениях случайных чисел а₁, а₂, …, а_n, которые могут быть взяты из специальных таб­лиц или получены с помощью специальных датчиков. Таким образом, выходной параметр, характеризующий работоспособность РЭА, оказывается функцией случай­ных чисел:

у = y(a₁, a₂,…, a_n).

Осуществляя N независимых реализации (испыта­ний) последовательности случайных чисел a₁, a₂,…, a_n:

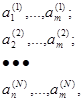
вычисляют для каждой из них значения y_i=y(a 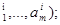1£ i£ N (верхний индекс у a обозначает номер реали­зации). Поскольку обработка числовых результатов является весьма трудоемкой, то процесс вычислений це­лесообразно автоматизировать, для чего разработанные алгоритмы программируются, т. е. предусмотренные ими операции представляются в системе определенных команд, которые позволяют произвести все расчеты с по­мощью ЭВМ.

По результатам N испытаний оценивают вероятность попадания параметра у в область А.

При числе попаданий К в область А

(13)

Установлено, что погрешность испытаний имеет порядок

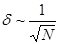. (14)

Если значения случайных величин имеют распреде­ление по нормальному закону, то погрешность, даваемая методом Монте-Карло, имеет вид:

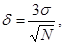(15)

где s - среднее квадратическое отклонение.

Повышение точности результатов испытаний дости­гается увеличением числа испытаний (N). Данный метод позволяет использовать сколь угодно сложную мате­матическую модель испытываемого устройства, достаточ­но полно отражающую физику его работы и уменьшаю­щую погрешности, свойственные расчетным методам. Математическая модель может, быть дана в виде систе­мы частных аналитических зависимостей отдельных вы­ходных параметров схемы от входных в виде эксперимен­тально полученных графиков, таблиц и т. п. Применение данного метода испытаний позволяет сконструировать более надежную РЭА и отказаться от ряда сложных лабораторных испытаний. Недостатками метода являют­ся необходимость наличия ЭВМ, обладающей большим быстродействием; определение основных соотношений, получаемых в результате больших предварительных тео­ретико-экспериментальных исследований, характеризую­щих математическую модель устройства; знание вероят­ностных характеристик входных (первичных) параметров.

Метод статистических испытаний физи­ческим моделированием РЭА предусматривает проведение испытаний на реальных аппаратах или на электронных моделях. При испытаниях на реальных аппаратах производят исследование процессов возникно­вения отказов в РЭА и их последствий путем искусст­венного введения в схему обрывов, коротких замыканий или установки элементов несоответствующих номиналов. Проведение испытаний на электронных моделях заклю­чается в том, что определенные элементы схемы заме­няются физическими моделями, позволяющими изменять величины характеризующих их параметров. Так, напри­мер, на рисунке 7 приведены схемы макетов элементов, позволяющие имитировать различные сопротивления ре­зисторов с помощью переменных резисторов, различные емкости и потери с помощью переменных конденсаторов и резисторов, разброс полупроводниковых диодов с по­мощью переменных резисторов.

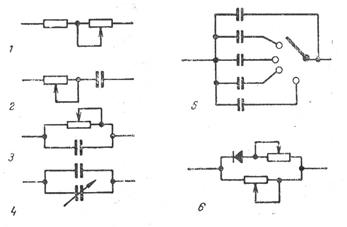
Рисунок 7 – Схемы макетов элементов

1 - резистор; 2,3 – конденсаторы постоянной емкости; 4,5 – конденсаторы переменной емкости; 6 – диод.

Моделирование различных элементов осуществляют на специальных стендах, позволяющих воспроизводить случайные процессы изменения параметров элементов. Для получения случайных процессов изменения напряжений, управляющих параметрами элементов, использу­ют специальные генераторы случайных процессов. До­стоинством данного метода является то, что отпадает необходимость в математической модели, связывающей выходные параметры с входными (первичными). Ука­занная связь реализуется непосредственно в физической модели.

Недостатками метода являются техническая слож­ность выполнения физических моделей ряда устройств (например, высокочастотных, импульсных и т. д.), вы­сокая стоимость стендов для проведения испытаний из-за их сложности и большой трудоемкости. Рассмотрен­ные статистические методы испытаний могут применять­ся как для моделирования процессов, происходящих внутри РЭА, так и для.моделирования внешних воздей­ствий, которым подвергается РЭА во время эксплуата­ции. При этом считают, что внешние воздействия опре­деляются обслуживающим персоналом и условиями работы РЭА. Для оценки процессов обслуживания, помимо статистических методов испытаний, применяют метод, называемый теорией массового обслуживания, а также составляются дифференциальные уравнения, отражающие динамику технического обслуживания.

1.8. ГРАНИЧНЫЕ ИСПЫТАНИЯ

Все виды испытаний и исследований, применяе­мые для предсказания места и времени появления посте­пенного отказа элемента или РЭА, основанные на определении связи граничных значений параметров эле­ментов с работоспособностью и надежностью РЭА, при­нято называть граничными испытаниями.

Пользуясь методом граничных испытаний возможно еще в процессе разработки РЭА выбрать оптимальные варианты схем, параметры их элементов и режимов. Граничные испытания являются экспериментальным ме­тодом, основанным на физическом моделировании обла­сти значений первичных параметров, при которых вы­ходные параметры устройства находятся в пределах до­пуска.

Проведение граничных испытаний складывается из следующих этапов:

1. Определение критериев отказа РЭА исходя из усло­вий работы и в соответствии с техническим заданием.

2. Определение границ работоспособности и надеж­ности РЭА, выполненного из элементов с номинальными параметрами, в зависимости от изменений напряжения питания, внешних условий, параметров входных сигна­лов.

3. Определение границ работоспособности и надеж­ности РЭА, работающего в нормальных условиях (номи­нальные напряжения питания, параметры входных сиг­налов и внешние условия), в зависимости от разброса параметров элементов РЭА.

Для осуществления граничных испытаний необходимо имитировать изменение параметров различных схемных элементов (резисторов, конденсаторов, катушек индук­тивности, электронных и полупроводниковых приборов), влияющих на работоспособность РЭА. Наиболее часто в качестве граничного параметра в данном методе вы­бирают одно из питающих напряжений (параметр гра­ничного испытания), которое используется для имитации изменений параметров элементов схемы (например, резисторов).

Изменение параметров конденсаторов и катушек индуктивности имитируют последовательно-параллельным включением этих элементов. Имитацию изменения пря­мого и обратного тока полупроводниковых приборов осуществляют последовательным или параллельным включением в схему дополнительных резисторов соответствующих номиналов и т. д.

Наибольшую сложность представляет имитация изменения параметров транзисторов и электронных ламп, так как они характеризуются сложной совокупностью параметров. В этих случаях подбирают группу элементов с одинаковыми параметрами, за исключением одного элемента, параметры которого изменяют в нужном на­правлении. Так, например, амплитуду напряжения сигнала на выходе лампового усилителя можно имитировать изменением напряжения анодного питания.

Рассмотрим определение границ исправной работы РЭА. Изменяя напряжение граничного испытания до момента отказа схемы при поминальных значениях па­раметров всех элементов, определим напряжение отка­за U_гр0. Затем, изменив один из параметров рассматри­ваемого элемента, определим, при каком новом значении U`_гр возникнет отказ. Очевидно, что при разных значе­ниях параметра (x₁, х₂,..., х_i, …, х_n) элемента отказы схемы будут возникать при различных напряжениях.

Таким образом, можно установить, что определенно­му отклонению напряжения граничного испытания DU_гр= U_грi- U_гр0 соответствует определенное значение Dx - отклонение параметра элемента от номинала.

По данным испытании строят график зависимости отклонения напряжения граничного испытания до отказа схемы (рисунок 8).

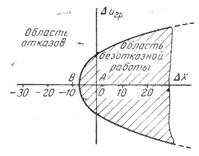
Рисунок 8 – график граничного испытания

Из графика следует, что кривая явля­ется границей, отделяющей область безотказной рабо­ты от области отказов, что и привело к названию - метод граничных испытаний. Следует отметить, что вид графика граничного испытания имеет существенное зна­чение для возможности его использования. При выборе напряжения граничного испытания необходимо, чтобы изменение величины параметра обеспечивало малый и плавный наклон кривой к оси отклонения параметра эле­мента (рисунок 9).

Рисунок 9 – Предсказание отказа при граничном испытании

Если при изменении указанного на­пряжения линия граничного испытания сначала остается постоянной, а затем резко падает до нуля, исключается возможность получения своевременной информации о приближении отказа и возникает необходимость ново­го подбора напряжения граничного испытания. В большинстве случаев при изменении параметров граничных испытаний в широких пределах контур без­отказной работы оказываются замкнутым (рисунок 10).

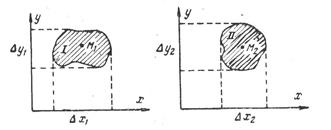
Рисунок 10 – Возможный вид замкнутого контура области безотказной работы

Знание графиков граничных испытаний позволяет определить «запас прочности» схемы, правильно выбрать номиналы параметров и режимы элементов схемы, пред­сказать появление постепенных отказов, а также сравнить надежность идентичных схем по площадям безот­казной работы.

Выбор номинала параметра часто заключается в опре­делении рабочей точки (М) в центре области безотказ­ной работы. Однако возможны случаи, когда выбор та­кого положения рабочей точки окажется неверным. Так, например, при дрейфе параметра элемента в определен­ном направлении необходимо предусматривать сдвиг рабочей точки в противоположном направлении. Обыч­но график граничных испытаний снимают при условии, что параметры всех схемных элементов, кроме подвер­гаемого испытанию, фиксированы. В реальных условиях изменения параметров сильно взаимосвязаны между со­бой и сдвиг параметра одного элемента может вызвать опасный с точки зрения надежности сдвиг другого. По­этому при осуществлении граничных испытаний РЭА приходится проводить боль­шой объем работы по опре­делению областей безотказ­ной работы ряда элементов. Полученные области накла­дывают друг на друга и окончательно область безотказной работы определяется общим геометрическим ме­стом точек для всех обла­стей (рисунок 11).

Date: 2015-07-17; view: 843; Нарушение авторских прав