Кратность резервирования и основные расчетные формулы

Кратность резервирования является основным параметром резервирования, определяемым как m / n – отношение числа резервных цепей к числу основных (резервируемых).

Как указано ранее (п.6.1), различают резервирование с целой и дробной кратностью. При резервировании с целой кратностью указывается величина m как целое число; при резервировании с дробной кратностью величина m представляется в виде несокращаемой дроби. Например, 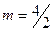означает, что имеется резервирование с дробной кратностью, при котором число резервных элементов равно четырем, число основных- двум, а общее их число равно шести. Дробь не сокращается, так как если 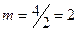, то это означает наличие резервирования с целой кратностью, равной двум, при общем числе элементов, равном трем.

Резервирование по способу включения может быть постоянным или резервированием замещением.

При постоянном резервировании резервные элементы подключены к основным в течение всего времени работы и работают в одинаковом с ними режиме.

При резервировании замещением резервные элементы замещают основные после их отказа.

Включение резерва по способу замещения свидетельствует о том, что рез6ервные элементы до момента включения их в работу могут находиться в трех состояниях:

- нагруженном резерве;

- облегченном резерве;

- ненагруженном резерве.

Для известных методов резервирования используются следующие расчётные формулы.

1. Для общего резервирования с постоянно включенным (нагруженным) резервом и с целой кратностью

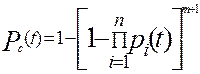, (6.1)

где p_i (t) – вероятность безотказной работы i -го элемента в течение времени t;

n - число элементов основной или любой резервной цепи;

Кратность резервирования m / n – отношение числа резервных цепей к числу основных (резервируемых). Дробь не сокращается.

При экспоненциальном законе надежности, когда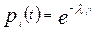

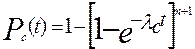,(6.2)

,

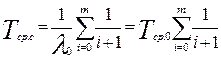где – 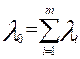интенсивность отказов нерезервированной системы или любой из m резервных систем; T _{cp. 0} – среднее время безотказной работы нерезервированной системы или любой из т резервных систем. При резервировании неравнонадежных изделий

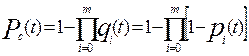, (6.3)

где q_i(t), p_i(t) – вероятность отказов и вероятность безотказной работы в течение времени t i - го изделия соответственно.

2. Раздельное резервирование с постоянно включенным резервом и с целой кратностью(рис. 6.1,6):

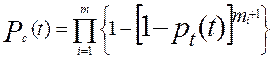, (6.4)

где p_i (t) – вероятность безотказной работы i - го эле­мента; m_i – (кратность резервирования i -го элемента; n – число элементов основной системы.

Приэкспоненциальном законе надежности, когда ,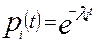

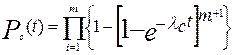
(6.5)

При равнонадежных элементах и одинаковой кратности их резервирования

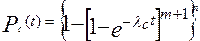, (6.6)

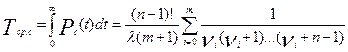, (6.7)

где ν_i=(i +1)/(m +1).

3. Общее резервирование замещением с целой крат­ностью (рис. 6.1,в):

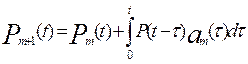(6.8)

где P_{m+ 1} (t), P_m(t), —вероятности безотказной работы резервированной системы кратности m+ 1 и m соответ­ственно; P(t-τ) — вероятность безотказной работы ос­новной системы в течение времени (t-τ); а_m(τ) — час­тота отказов резервированной системы кратности m в момент времени τ.

Формула (6.8) позволяет получить рас­четные соотношения для устройств любой кратности ре­зервирования. Для получения таких формул необходимо выполнить интегрирование в правой части, подставив вместо P(t-τ) и a_m(τ) их значения в соответствии с выбранным законом распределения и состоянием ре­зерва.

При экспоненциальном законе надежности иненагруженном состоянии резерва

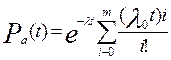, (6.9)

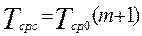, (6.10)

где λ₀, Т_ср.0 — интенсивность отказов и средняя наработ­ка до первого отказа основного (нерезервированного) устройства.

При экспоненциальном законе инедогруженном со­стоянии резерва

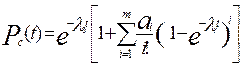, (6.11)

, (6.12)

где 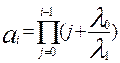; ; 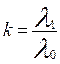λ₁ — интенсивность отказов резервного устройства до замещения.

При нагруженном состоянии резерва формулы для Р_с (t)и Т_{ср. с} совпадают с (6.2).

4. Раздельное резервирование замещением с целой кратностью (рис. 6.1,г):

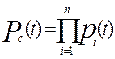, (6.13)

где p_i(t) — вероятность безотказной работы системы из-за отказов элементов i -го типа, резервированных по способу замещения. Вычисляется p_i(t) по формулам общего резервирования замещением (формулы (6.8),(6.9), (6.11)).

5. Общее резервирование с дробной кратностью и по­стоянно включенным резервом (рис. 6.1, д):

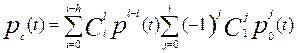, (6.14)

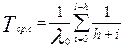, (6.15)

где p₀(t) – вероятность безотказной работы основного или любого резервного элемента; l – общее число основных и резервных систем; h – число систем, необходимых для нормальной работы резервированной системы.

В данном случае кратность резервирования

m= (l-h)/h ( 6.16)

1. Скользящее резервирование:

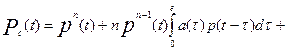
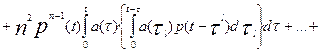
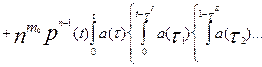
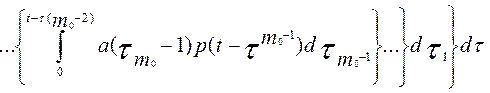, (6.17)

где τ^I = τ + τ₁ ; τ^II = τ+ τ₁+ τ₂…; 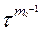= τ + τ₁+…+ 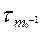; n – число элементов основной системы; m₀ — чис­ло резервных элементов; p(t - t_i) —вероятность безотказ­ной работы одного элемента в течение времени (t - t_i); t_i= t, t – τ, 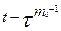; a(τ_i) — частота отказов одного из основных элементов в момент времени τ_i, 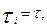τ ₁, …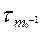

При экспоненциальном законе надежности

=

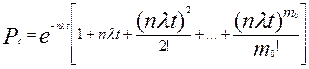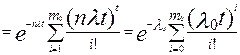; (6.18)

Т_ср.с=Т_ср.0(m₀+1),

где λ₀ = nλ – интенсивность отказов нерезервированной системы; λ – интенсивность отказов элемента; n – число элементов основной системы; T _cp.0 –среднее время безотказной работы нерезервированной системы; m₀ – число резервных элементов. В этом случае кратность резервирования

m = m₀ /n (6.19)

Приведенные выше формулы (кроме (6.8), (6.11), (6.12)) могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последействия отказов.

Последействия отказов сказываются практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва.

Выражение (6.8) является основным при получении расчетных формул в случае учета влияния последействия отказов. При этом члены p(t-τ) и а_m(τ) должны быть записаны с учетом последействия отказов, вида резервирования и его кратности.

Элементы резервированных устройств в ряде случаев могут иметь два вида отказов — «обрыв» и «короткое замыкание». В этом случае вычислять вероятность безотказной работы следует, суммируя вероятности всех благоприятных (не приводящих к отказу) гипотез, т. е.

, (6.20)

где p_j (t) – вероятность j - й благоприятной гипотезы, вычисленной с учетом двух видов отказав; k – число благоприятных гипотез.

При вычислениях p_j (t) следует иметь в виду, что для элементов сложной системы справедливы выражения

, φ₀ + φ_з = 1 (6.21)

где l (t) – нтенсивность отказов элемента; φ₀, φ_з – вероятность возникновения «обрыва» и «короткого замыкания», соответственно.

При экспоненциальном законе надежности

p(t)= e^-λt, 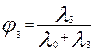, , 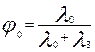(6.22)

где λ₀, λ₃ – интенсивность отказов элемента по «обрыву» и «короткому замыканию», соответственно.

Остальные количественные характеристики надежности в случае необходимости вычисляются через P_c(t) по известным аналитическим зависимостям, приведенным в гл. 1.

Расчет надежности резервированных систем иногда полезно выполнять, используя схему «гибели» («чистого размножения»). В соответствии с этой схемой преобразование Лапласа вероятности возникновения п отказов вычисляется по формуле

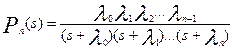. (6.23)

При неравных корнях знаменателя обратное преобразование Лапласа P_n(s) будет

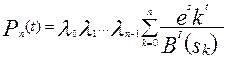. (6.24)

В формулах (6.23) и (6.24) приняты обозначения: λ₀ – интенсивность отказов системы до выхода из строя первого элемента; λ₁ – интенсивность отказов системы в промежутке времени от момента отказа первого элемента до второго; λ₂ – интенсивность отказов системы в промежутке времени от момента отказа второго эле­мента до третьего и т. д.; п – число отказавших элементов;

s_k= - λ_h - k – k - й корень знаменателя выражения (6.23);

B'(s_k) - производная знаменателя в точке s_k.

При одинаковых опасностях отказов λ_i, т. е λ₀ = λ₁ = λ₂ =…=λ_n, расчетные формулы имеют вид

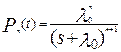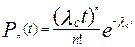, . (6.25)

При расчетах надежности по формулам (6.23) — (6.25) следует помнить, что они не определяют вероятности безотказной работы (или вероятности отказа) резервированной системы, а определяют лишь вероятность i -го состояния системы, т. е. вероятность того, что в системе откажут п элементов. Для вычисления вероятности безотказной работы необходимо находить вероятности 0, 1,..., n отказов, когда система еще находится в работоспособном состоянии (исправна), я суммировать полученные вероятности.

Среднее время безотказной работы системы при использовании схемы «гибели» вычисляется по формуле

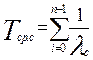; (6.26)

где λ_i – интенсивность отказов системы до выхода из строя i - го элемента.

При схемной реализации резервирования в ряде случаев конкретные технические решения не приводятся к логическим схемам расчёта надёжности (рис. 5.1, 5.2, 5.4, 5.5).

В этих случаях следует для получения аналитических выражений для количественных характеристик надежности использовать метод перебора благоприятных гипотез. Вероятность безотказной работы в этом случае вычисляется по выражению (6.20).

При анализе надежности резервированных устройств на этапе проектирования приходится сравнивать различные схемные решения. В этом случае за критерий качества резервирования принимается выигрыш надежности.

Выигрышем надежности называется отношение количественной характеристики надежности резервированного устройства к той же количественной характе­ристике нерезервированного устройства или устройства с другим видом резервирования.

Наиболее часто используются следующие критерии качества резервированных устройств: G₀ (t) i — выигрыш надежности в течениевремени t по вероятности отказов; G₀ (t) выигрыш надежности в течение времени t по вероятности безотказной работы; G _T — выигрыш надежности по среднему времени безотказной работы.

При резервировании элементов электроники (резисторов, конденсаторов, контактов реле, диодов и т. п.) всегда произведение интенсивности отказов элемента на время его работы значительно меньше единицы, т. е. λt ˂˂ 1 Поэтому (при вычислении G_q(t) и G_q(p) целесообразно функции вида e^-kλt (экспоненциальный случай) разложить в ряд:

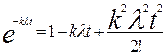(при небольшом k).

Если система исправна при отказе т элементов, то необходимо брать не менее чем m +2 членов разложения.

Пример 6.1. Дана система, схема расчета надежности которой изображена на рисунке 6.1. Необходимо найти вероятность безотказной работы системы при известных вероятностях безотказной работы ее элементов (значе­ния вероятностей указаны на рисунке).

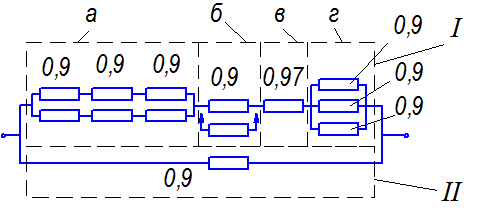
Рис. 6.2 Схема расчета надежности

Решение. На рис. 6.2 видно, что система состоит из двух (I и II) неравнонадежных устройств. Устройство I состоит из четырех узлов: а - дублированного узла с постоянно включенным резервом, причем каждая часть узла состоит из трех последовательно соединенных (в смысле надежности) элементов расчета;

б - дублированного узла то способу замещения;

в - узла с одним нерезервированным элементом;

г - резервированного узла с кратностью m =1/2 (схе­ма группирования).

Устройство II представляет собой нерезервированное устройство, надежность которого известна.

Так как оба устройства неравнонадежны, то на осно­вании формулы (6.3) имеем

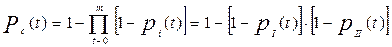
Определяется вероятность p_I(t). Вероятность безотказной работы устройства I равна произведению вероятностей безотказной работы всех узлов, то есть

p_I (t) = р_ар_бр_вр_г.

В узле а число элементов основной и резервной цепи n = 3, а кратность резервирования т = 1. Тогда на осно­вании формулы (6.1)

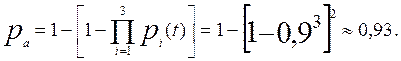
В узле б кратность общего резервирования замеще­нием т= 1, тогда на основании формулы (6.9) имеем

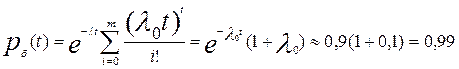
В узле г применено резервирование с дробной крат­ностью, когда общее число основных и резервных систем l = 3, число систем, необходимых для нормальной ра­боты, h =2. Тогда на основании формулы (6.14)

Вероятность безотказной работы устройства I будет

р_х = р_ар_бр_вр, = 0,93٠ 0,99٠ 0,97٠ 0,972 ≈ 0,868

Тогда вероятность безотказной работы резервирован­ной системы будет

P ₀ = l - (l - p _I) (1- р _II ) -1- (1 — 0,868) (1- 0,9) = 0,987.

Пример 6.2. Вероятность безотказной работы преоб­разователя постоянного тока в переменный в течение t = 1000 ч равна 0,95, т. е. Р (1000) = 0,95. Для повышения надежности системы электроснабжения на объек­те имеется такой же преобразователь, который включа­ется в работу при отказе первого. Требуется рассчитать вероятность безотказной работы и среднюю наработку до первого отказа системы, состоящей из двух преобра­зователей, а также построить зависимости от времени частоты отказов f_c (t)и интенсивности отказов l_c(t) си­стемы.

Решение. Из условия задачи видно, что имеет ме­сто общее резервирование замещением кратности т= 1. Тогда на основании формулы (6.9) получается

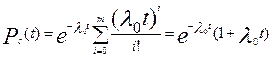
Из условия задачи 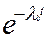= 0,95, тогда λ₀ (t) ≈ 0,05. Под­становка значения Р (1000) и полученного значения λ₀ (t)в выражение для Р_с (t), позволяет получить

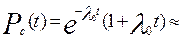0,95 (1+ 0,05) = 0,9975.

Средняя наработка до первого отказа системы на основании формулы (6.10)

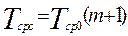= 2 T_{ср .0.}

Так как в течение времени t = 1000 ч и λ ₀ t = 0,05, то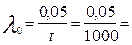

=0,5٠10^-4 ч ^-1, а средняя наработка до первого отказа нерезервированного преобразова­теля Т_{ср. 0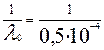} = = 20000 ч.

Тогда средняя наработка до первого отказа резерви­рованной системы

Т _{ср. с} = 2 Т _ср.0 = 40 000 ч.

Для построения графиков f_c(t) и λ _c (t) находятся ана­литические выражения этих функций по известной вероятности безотказной работы системы:

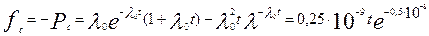
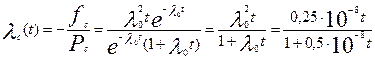
Графики f_c(t) и λ _c (t) приведены на рис. 6.3.

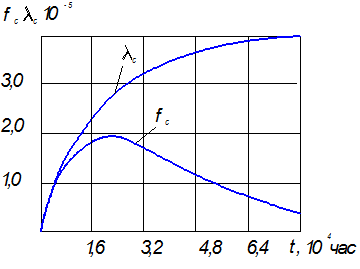
Рис. 6.3 Зависимость f_с и λ _cот t

Количественно повышение надежности системы в результате резервирования или применения высоконадежных элементов можно оценить по коэффициенту выигрыша надежности, определяемому как отношение показателя надежности до и после преобразования системы. Например, для системы из n последовательно соединенных элементов после резервирования одного из элементов (k -го) аналогичным по надежности элементом коэффициент выигрыша надежности по вероятности безотказной работы составит:

,

где Р^'- вероятность безотказной работы резервированной системы,

Р - вероятность безотказной работы нерезервированной системы.

Из формулы (6.27) следует, что эффективность резервирования (или другого приема повышения надежности) тем больше, чем меньше надежность резервируемого элемента (при , , ).

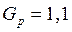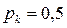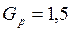Следовательно, при структурном резервировании наибольшего эффекта можно добиться при резервировании самых ненадежных элементов (или групп элементов).

В общем случае при выборе элемента (или группы элементов) для повышения надежности или резервирования необходимо исходить из условия обеспечения при этом наилучшего результата.

Date: 2015-07-17; view: 14664; Нарушение авторских прав