Частота Найквиста, теорема Котельникова

Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано академиком В.А.Котельниковым: "Любая непрерывная функция s(t), спектр которой ограничен частотой F_max полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 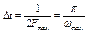". Частота 2F_max называется частотой Найквиста. Кроме того, теорема Котельникова дает и способ точного восстановления сигнала 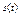по его отсчетам: , где

Максимальные значения членов ряда будут при и равны , при этом все остальные члены ряда равны нулю, т. е. при 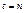функция s (t) точно передается рядом. Во все другие моменты времени необходимо суммировать бесконечное число отсчетов, чтобы передать s (t)точно.

Представление сигнала в виде ряда Котельникова является частным случаем разложения Фурье . Роль коэффициента выполняют отсчеты Базисными являются функции вида . Они называются функциями отсчетов.

Практическое осуществление дискретизации сигнала s (t) рядом Котельникова и дальнейшее его восстановление сводится к следующему. На передающей стороне через интервалы D определяются мгновенные значения сигнала и передаются в канал связи в виде импульсов с площадью, равной отсчету . На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот . При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал s (t).

Искажения восстановленного (по Котельникову) сигнала могут происходить по следующим причинам. Реальный сигнал имеет конечную длительность и, следовательно, обладает неограниченным спектром. Дискретизация его с интервалом D ограничивает спектр и, следовательно, искажает воспроизведение сигнала. С другой стороны, и при передаче непрерывного сигнала вследствие ограничения полосы пропускания аппаратуры сигнал искажается. Однако при дискретизации появляется дополнительное искажение за счет конечности числа отсчетов за ограниченное время длительности сигнала, в то время как их должно быть бесконечно много, т. к. ограничению спектра сигнала соответствует увеличение его длительности до бесконечности. Такое двойное искажение хотя и может частично компенсироваться, но создает трудности для теоретического анализа погрешности передачи.

Несмотря на невозможность точного воспроизведения сигнала ограниченной длительности (чем более короткий сигнал, тем больше ошибка воспроизведения), дискретизация и восстановление по Котельникову используется весьма широко при преобразовании сигнала в цифровую форму.

Date: 2016-08-30; view: 409; Нарушение авторских прав