Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Способы задания линейных кодов
|
|
1. Перечислением кодовых слов, т.е. составлением списка всех кодовых слов кода.
Пример. В таблице справа представлены все кодовые слова (5,3)-кода (ai - информационные, а bi - проверочные символы).
| № п/п | a1 | a2 | a3 | b1 | b2 |
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:
, где
j ‑ номер проверочного символа;
i ‑ номер информационного символа;
hij ‑ коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
b1= a2 + a3; b2= a1 + a2.
3. Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF (2) включает в себя 2 n векторов (n -последовательностей), а подпространством его является множество из 2 k кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n, k) - код полностью определяется набором из k кодовых слов, принадлежащих этому коду.
Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) - код, который был представлен в таблице 1, может быть задан матрицей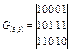 
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением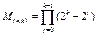 
Для исключения неоднозначности в записи G (n, k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид
, где Ik ‑ единичная матрица, содержащая информационные символы; Rk,r ‑ прямоугольная матрица, составленная из проверочных символов.
Пример. Порождающая матрица в систематическом виде для (5,3) – кода 
Порождающая матрица G(n,k) в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид 
, где Ir ‑ единичная матрица; 
‑ прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
Пример. Проверочная матрица (5,3) – кода 
Date: 2016-08-30; view: 575; Нарушение авторских прав